椭圆
图片预览





文档简介
课件13张PPT。方法一:基本法,其一般步骤是:1、建系、设点、画图2、翻译、列式、化简3、舍增、补遗、作结一.复 习 旧 知 方法二:待定系数法,其一般步骤是: 先设方程再求参数后写出方程求动点轨迹方程的方法:2002年11月3号永宁回民中学 周学梅 椭圆及其标准方程椭圆的定义:
我们把平面内与两个定点F1,F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距.
二.新课学习三.方程推导解:取过焦点F1,F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立直角坐标系(如图). 设M(x,y)是椭圆上任
意一点,椭圆的焦距为
2c(c>0),M与F1和F2的
距离的和等于正常数2a,
则F1,F2的坐标分别是
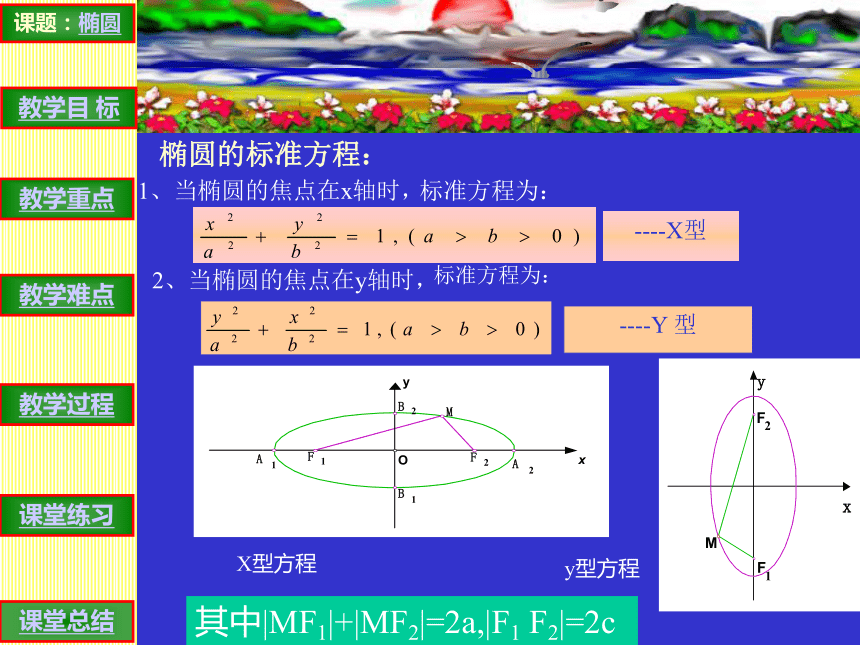
(?c,0)(c,0) 。得方程 两边再平方,得 : 整理得: 将方程移项,两边平方,得 :两边除以:由椭圆的定义可知,2a>2c,即a>c,所以 : a2—c2>0,设椭圆的标准方程: 1、当椭圆的焦点在x轴时, ----X型2、当椭圆的焦点在y轴时, ----Y 型X型方程y型方程标准方程为:标准方程为:其中|MF1|+|MF2|=2a,|F1 F2|=2c四.应用举例例1.(1)求出满足a=5,b=4,焦点在x轴上的椭圆的标准方程。(2)求出满足a=10,c=6,焦点在y轴上的椭圆的标准方程。教学过程 (3)、已知椭圆 上一点,P到椭圆一个焦点的距离为3,则P到另一个焦点的距离是( )
A 2 B 3 C 5 D 7 (4)、椭圆 的焦距为2,则m的值为( )
A 5 B 3 C 3或5 D 6DC(5)、已知F1,F2是椭圆 的两个焦点,AB是过F1的弦,则三角形ABF2的周长是_____.教学过程(6)、已知?ABC的周长为36,且AB长为10,求?ABC的顶点C的轨迹方程。20(y?0)例2 平面内两个定点的距离是8,写出到这两个定点的距离的和是10的点的轨迹方程解:建立坐标系如
图所示由椭圆的定义易知:
a=5,c=4,b=3故所求椭圆的方程是:(1)因为x项的分母大,故椭圆的焦点在x轴上。其中a=5,b=4,c=3(2)因为y项的分母大,故椭圆的焦点在y轴上。其中a=10,b=8,c=6 五.课堂练习1、判断下列各椭圆的焦点所在的坐标轴并指出a、 b、c的值 六.课堂总结:1、椭圆的定义 2、椭圆的标准方程 平面内点M与两个定点F1、F2的距离的和等于常数(记|MF1|+|MF2|=2a)的点M的轨迹是: (1)当|MF1|+|MF2|>|F1F2|时点M的轨迹是为_____; (2)当|MF1|+|MF2|=|F1F2|时点的轨迹为____________;. (3)当|MF1|+|MF2|<|F1F2|时点M的轨迹________。其中椭圆的焦点的位置由__________________________ 来确定。-----X型----Y 型椭圆线段F1F2不存在X2、y2项的分母的大小七.作业:1、第96页 2. 3题2、已知?ABC的一边BC长为6,周长为16,求顶点A的轨迹方程。
我们把平面内与两个定点F1,F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距.
二.新课学习三.方程推导解:取过焦点F1,F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立直角坐标系(如图). 设M(x,y)是椭圆上任
意一点,椭圆的焦距为
2c(c>0),M与F1和F2的
距离的和等于正常数2a,
则F1,F2的坐标分别是
(?c,0)(c,0) 。得方程 两边再平方,得 : 整理得: 将方程移项,两边平方,得 :两边除以:由椭圆的定义可知,2a>2c,即a>c,所以 : a2—c2>0,设椭圆的标准方程: 1、当椭圆的焦点在x轴时, ----X型2、当椭圆的焦点在y轴时, ----Y 型X型方程y型方程标准方程为:标准方程为:其中|MF1|+|MF2|=2a,|F1 F2|=2c四.应用举例例1.(1)求出满足a=5,b=4,焦点在x轴上的椭圆的标准方程。(2)求出满足a=10,c=6,焦点在y轴上的椭圆的标准方程。教学过程 (3)、已知椭圆 上一点,P到椭圆一个焦点的距离为3,则P到另一个焦点的距离是( )
A 2 B 3 C 5 D 7 (4)、椭圆 的焦距为2,则m的值为( )
A 5 B 3 C 3或5 D 6DC(5)、已知F1,F2是椭圆 的两个焦点,AB是过F1的弦,则三角形ABF2的周长是_____.教学过程(6)、已知?ABC的周长为36,且AB长为10,求?ABC的顶点C的轨迹方程。20(y?0)例2 平面内两个定点的距离是8,写出到这两个定点的距离的和是10的点的轨迹方程解:建立坐标系如
图所示由椭圆的定义易知:
a=5,c=4,b=3故所求椭圆的方程是:(1)因为x项的分母大,故椭圆的焦点在x轴上。其中a=5,b=4,c=3(2)因为y项的分母大,故椭圆的焦点在y轴上。其中a=10,b=8,c=6 五.课堂练习1、判断下列各椭圆的焦点所在的坐标轴并指出a、 b、c的值 六.课堂总结:1、椭圆的定义 2、椭圆的标准方程 平面内点M与两个定点F1、F2的距离的和等于常数(记|MF1|+|MF2|=2a)的点M的轨迹是: (1)当|MF1|+|MF2|>|F1F2|时点M的轨迹是为_____; (2)当|MF1|+|MF2|=|F1F2|时点的轨迹为____________;. (3)当|MF1|+|MF2|<|F1F2|时点M的轨迹________。其中椭圆的焦点的位置由__________________________ 来确定。-----X型----Y 型椭圆线段F1F2不存在X2、y2项的分母的大小七.作业:1、第96页 2. 3题2、已知?ABC的一边BC长为6,周长为16,求顶点A的轨迹方程。
