人教版八年级数学上册 11.3.1 多边形教学课件(共18张ppt)
文档属性
| 名称 | 人教版八年级数学上册 11.3.1 多边形教学课件(共18张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 459.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-20 16:33:54 | ||
图片预览



文档简介
(共18张PPT)
第十一章 三角形
11.3 多边形及其内角和
11.3.1 多边形
三角形的外角与内角的关系:
1. 三角形的一个外角与它相邻的内角 ;
互补
2. 三角形的一个外角 与它不相邻的两个内角的和;
等于
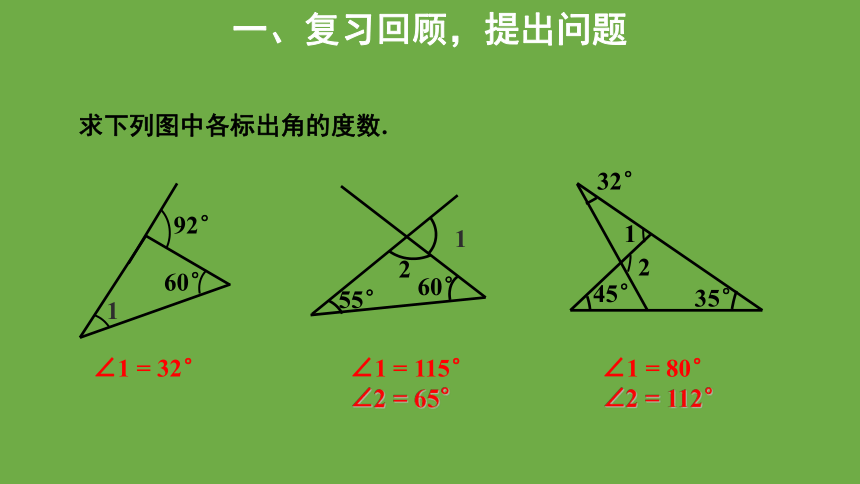
一、复习回顾,提出问题
求下列图中各标出角的度数.
92°
60°
1
1
55°
60°
2
1
2
45°
35°
32°
∠1 = 32°
∠1 = 115°
∠2 = 65°
∠1 = 80°
∠2 = 112°
一、复习回顾,提出问题
你能从图中想象出几个由一些线段围成的图形吗?
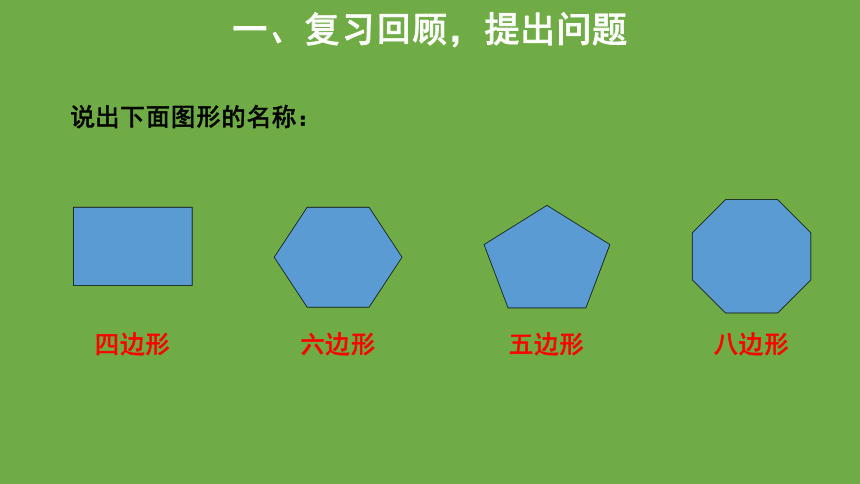
一、复习回顾,提出问题
说出下面图形的名称:
四边形
八边形
六边形
五边形
一、复习回顾,提出问题
多边形的定义:
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
二、合作交流,探究新知
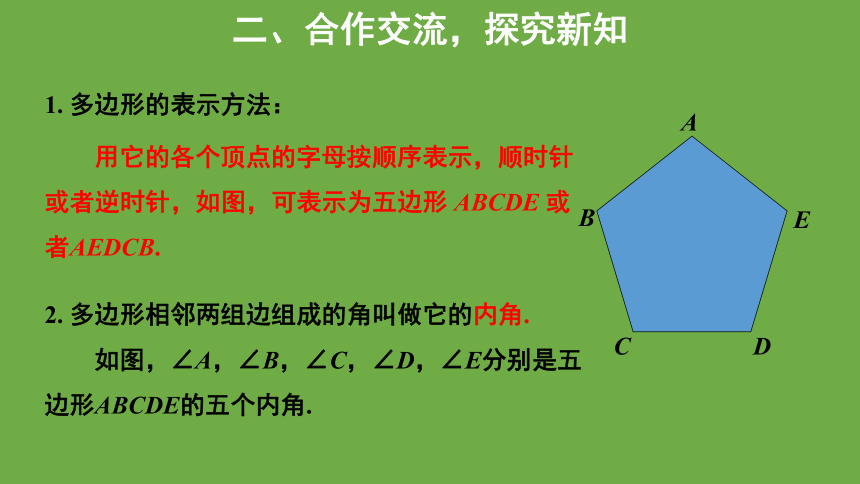
1. 多边形的表示方法:
A
B
C
D
E
用它的各个顶点的字母按顺序表示,顺时针或者逆时针,如图,可表示为五边形 ABCDE 或者AEDCB.
2. 多边形相邻两组边组成的角叫做它的内角.
如图,∠A,∠B,∠C,∠D,∠E分别是五边形ABCDE的五个内角.
二、合作交流,探究新知
3. 多边形的边与它的邻边的延长线组成的角叫多边形的外角.
A
B
C
D
E
如∠1就是五边形ABCDE的一个外角.
4. 连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
如图所示,AC,AD是多边形ABCDE的两条对角线.
1
二、合作交流,探究新知
请说出下列图形从某一顶点出发的对角线的条数:
三角形
六边形
四边形
八边形
……
五边形
二、合作交流,探究新知
n 边形对角线:
n 边形
……
三角形
四边形
五边形
六边形
从同一顶点引出的对角线的条数:
分割出的三角形的个数:
0
1
2
3
n - 3
1
2
3
4
n - 2
二、合作交流,探究新知
n 边形对角线:
(n-3)
n 边形共有对角线 条(n ≥ 3).
n 边形从一个顶点出发的对角线条数为: 条(n ≥ 3).
二、合作交流,探究新知
多边形的分类
如图,画出四边形ABCD的任何一条边所在直线,整个四边形都在这条直线的同一侧,这样的四边形叫做凸四边形.
A
B
C
D
二、合作交流,探究新知
多边形的分类
四边形ABCD是凹四边形,因为画出边CD(或BC)所在直线,整个四边形不都在这条直线的同一侧.
A
B
D
C
二、合作交流,探究新知
正多边形
正方形的各个角都相等,各条边都相等.
像正方形这样,各个角都相等,各条边都相等的多边形叫做正多边形.
例如:
正三角形
正方形
正五边形
正六边形
二、合作交流,探究新知
1. 如图,此多边形应记作_____边形____________,AB边的邻边是_______,_______,顶点E处的内角为__________,过顶点A画出这个多边形的对角线,共有_____条,它们把多边形分成_____个三角形.
A
B
C
D
E
五
ABCDE
AE
BC
∠AED
2
3
三、巩固新知
2. n 边形有______个顶点,_____边,有_____个角,有______个不共顶点外角.
3. 四边形有_____条对角线.五边形有______条对角线.四边形的一条对角线将它分成______个三角形.
4. 从五边形的一个顶点出发可以画_____条对角线,它们将五边形分成______个三角形.
5. 正多边形的_____相等,____相等.
6. 多边形分为___________和____________两类.
n
n
n
n
2
2
5
2
3
边
角
凹多边形
凸多边形
三、巩固新知
1. 多边形的定义
在平面内,由一些线段首尾顺次相接组成的图形.
2. 多边形的内角
多边形相邻两边组成的角.
3. 多边形的外角
多边形的一边与它相邻边的反向延长线组成的角.
4. 多边形的对角线
连接多边形不相邻的两个顶点的线段.
5. 正多边形
各个角相等,各条边都相等的多边形.
四、归纳小结
再 见
第十一章 三角形
11.3 多边形及其内角和
11.3.1 多边形
三角形的外角与内角的关系:
1. 三角形的一个外角与它相邻的内角 ;
互补
2. 三角形的一个外角 与它不相邻的两个内角的和;
等于
一、复习回顾,提出问题
求下列图中各标出角的度数.
92°
60°
1
1
55°
60°
2
1
2
45°
35°
32°
∠1 = 32°
∠1 = 115°
∠2 = 65°
∠1 = 80°
∠2 = 112°
一、复习回顾,提出问题
你能从图中想象出几个由一些线段围成的图形吗?
一、复习回顾,提出问题
说出下面图形的名称:
四边形
八边形
六边形
五边形
一、复习回顾,提出问题
多边形的定义:
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
二、合作交流,探究新知
1. 多边形的表示方法:
A
B
C
D
E
用它的各个顶点的字母按顺序表示,顺时针或者逆时针,如图,可表示为五边形 ABCDE 或者AEDCB.
2. 多边形相邻两组边组成的角叫做它的内角.
如图,∠A,∠B,∠C,∠D,∠E分别是五边形ABCDE的五个内角.
二、合作交流,探究新知
3. 多边形的边与它的邻边的延长线组成的角叫多边形的外角.
A
B
C
D
E
如∠1就是五边形ABCDE的一个外角.
4. 连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
如图所示,AC,AD是多边形ABCDE的两条对角线.
1
二、合作交流,探究新知
请说出下列图形从某一顶点出发的对角线的条数:
三角形
六边形
四边形
八边形
……
五边形
二、合作交流,探究新知
n 边形对角线:
n 边形
……
三角形
四边形
五边形
六边形
从同一顶点引出的对角线的条数:
分割出的三角形的个数:
0
1
2
3
n - 3
1
2
3
4
n - 2
二、合作交流,探究新知
n 边形对角线:
(n-3)
n 边形共有对角线 条(n ≥ 3).
n 边形从一个顶点出发的对角线条数为: 条(n ≥ 3).
二、合作交流,探究新知
多边形的分类
如图,画出四边形ABCD的任何一条边所在直线,整个四边形都在这条直线的同一侧,这样的四边形叫做凸四边形.
A
B
C
D
二、合作交流,探究新知
多边形的分类
四边形ABCD是凹四边形,因为画出边CD(或BC)所在直线,整个四边形不都在这条直线的同一侧.
A
B
D
C
二、合作交流,探究新知
正多边形
正方形的各个角都相等,各条边都相等.
像正方形这样,各个角都相等,各条边都相等的多边形叫做正多边形.
例如:
正三角形
正方形
正五边形
正六边形
二、合作交流,探究新知
1. 如图,此多边形应记作_____边形____________,AB边的邻边是_______,_______,顶点E处的内角为__________,过顶点A画出这个多边形的对角线,共有_____条,它们把多边形分成_____个三角形.
A
B
C
D
E
五
ABCDE
AE
BC
∠AED
2
3
三、巩固新知
2. n 边形有______个顶点,_____边,有_____个角,有______个不共顶点外角.
3. 四边形有_____条对角线.五边形有______条对角线.四边形的一条对角线将它分成______个三角形.
4. 从五边形的一个顶点出发可以画_____条对角线,它们将五边形分成______个三角形.
5. 正多边形的_____相等,____相等.
6. 多边形分为___________和____________两类.
n
n
n
n
2
2
5
2
3
边
角
凹多边形
凸多边形
三、巩固新知
1. 多边形的定义
在平面内,由一些线段首尾顺次相接组成的图形.
2. 多边形的内角
多边形相邻两边组成的角.
3. 多边形的外角
多边形的一边与它相邻边的反向延长线组成的角.
4. 多边形的对角线
连接多边形不相邻的两个顶点的线段.
5. 正多边形
各个角相等,各条边都相等的多边形.
四、归纳小结
再 见
