人教版八年级数学上册 十一章 数学活动 平面镶嵌(共42张ppt)
文档属性
| 名称 | 人教版八年级数学上册 十一章 数学活动 平面镶嵌(共42张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 715.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-20 20:48:32 | ||
图片预览










文档简介
(共42张PPT)
数学活动
平面镶嵌
第十一章 三角形
图案欣赏
图案欣赏
图案欣赏
平面镶嵌
从数学的角度看,用一些不重叠摆放的多边形把平面的一部分完整覆盖,叫做多边形覆盖平面(或平面镶嵌).
仅用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面?
问题1
尝试拼图
尝试拼图
尝试拼图
尝试拼图
尝试拼图
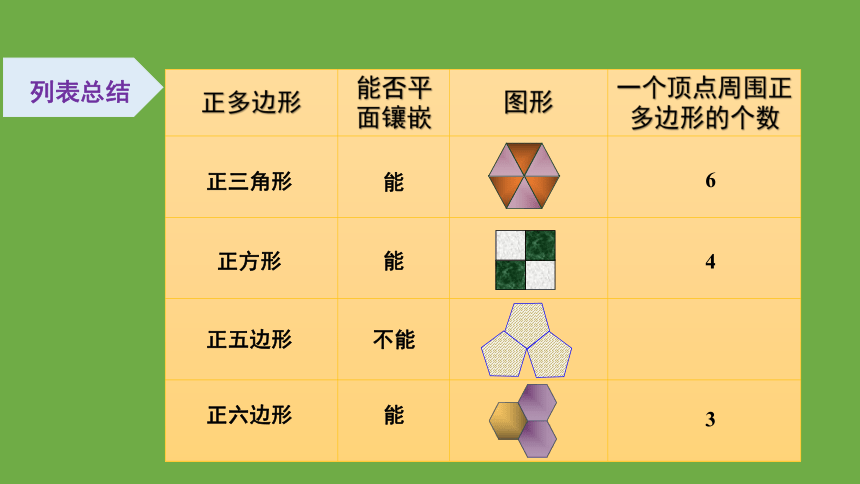
正多边形 能否平面镶嵌 图形 一个顶点周围正多边形的个数
能
能
能
正三角形
正方形
正五边形
正六边形
6
4
3
不能
列表总结
只用一种正多边形镶嵌有哪几种情形?
镶嵌的条件是?
一个顶点处的几个多边形的内角和是360°.
这种正多边形的一个内角的倍数是否是360°.
正三角形 正方形 正六边形
要用正多边形镶嵌成一个平面的关键是看:
规律总结
正多边形的边数n 3 4 5 6 7 8 9 10 12
每个内角的度数 60 90 108 120 135 140 140 144 150
设用m个全等的正n边形能镶嵌平面,则有
化简得
有且仅有三组正整数解:
即分别用6个正三角形、4个正方形、3个正六边形可以镶嵌平面.
数学道理
同一种形状大小相同的任意三角形可否镶嵌成一个平面?
同一种形状大小相同的任意四边形可否镶嵌成一个平面?
问题2
尝试拼图
尝试拼图
因为任一三角形的三个内角之和是180°,所以只要有六个全等三角形就可以拼成一块平面区域.
数学道理
因为任一四边形的四个内角之和是360°,所以只要有四个全等三角形就可以拼成一块平面区域.
用两种正多边形镶嵌,哪些能镶嵌成一个平面
问题3
(1)正三角形和正方形的组合
60°+60°+60°+90°+90°=360°
90°+90°+60°+60°+60°=360°
(1)正三角形和正方形的组合
(2)正三角形和正六边形的组合
120°+120°+60°+60°=360°
120°+60°+60°+60°+60°=360°
(2)正三角形和正六边形的组合
150°+150°+60°=360°
(3)正三角形和正十二边形组合
(4)正方形和正八边形组合
135°+135°+90°=360°
144°+108°+108°=360 °
(5)正五边形和正十边形的组合
正多边形的边数n 3 4 5 6 7 8 9 10 12
每个内角的度数 60 90 108 120 135 140 140 144 150
解不定方程其中是正多边形每个内角的度数,是对应正多边形的个数.
数学道理
用三种正多边形镶嵌,哪些能镶嵌成一个平面?
问题4
(1)正三角形、正方形和正六边形的组合
120°+90°+90°+60°=360 °
(2)正方形、正六边形和正十二边形的组合
150°+120°+90°=360 °
正多边形的边数n 3 4 5 6 7 8 9 10 12
每个内角的度数 60 90 108 120 135 140 140 144 150
解不定方程其中是正多边形每个内角的度数,是对应正多边形的个数.
数学道理
再见
数学活动
平面镶嵌
第十一章 三角形
图案欣赏
图案欣赏
图案欣赏
平面镶嵌
从数学的角度看,用一些不重叠摆放的多边形把平面的一部分完整覆盖,叫做多边形覆盖平面(或平面镶嵌).
仅用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面?
问题1
尝试拼图
尝试拼图
尝试拼图
尝试拼图
尝试拼图
正多边形 能否平面镶嵌 图形 一个顶点周围正多边形的个数
能
能
能
正三角形
正方形
正五边形
正六边形
6
4
3
不能
列表总结
只用一种正多边形镶嵌有哪几种情形?
镶嵌的条件是?
一个顶点处的几个多边形的内角和是360°.
这种正多边形的一个内角的倍数是否是360°.
正三角形 正方形 正六边形
要用正多边形镶嵌成一个平面的关键是看:
规律总结
正多边形的边数n 3 4 5 6 7 8 9 10 12
每个内角的度数 60 90 108 120 135 140 140 144 150
设用m个全等的正n边形能镶嵌平面,则有
化简得
有且仅有三组正整数解:
即分别用6个正三角形、4个正方形、3个正六边形可以镶嵌平面.
数学道理
同一种形状大小相同的任意三角形可否镶嵌成一个平面?
同一种形状大小相同的任意四边形可否镶嵌成一个平面?
问题2
尝试拼图
尝试拼图
因为任一三角形的三个内角之和是180°,所以只要有六个全等三角形就可以拼成一块平面区域.
数学道理
因为任一四边形的四个内角之和是360°,所以只要有四个全等三角形就可以拼成一块平面区域.
用两种正多边形镶嵌,哪些能镶嵌成一个平面
问题3
(1)正三角形和正方形的组合
60°+60°+60°+90°+90°=360°
90°+90°+60°+60°+60°=360°
(1)正三角形和正方形的组合
(2)正三角形和正六边形的组合
120°+120°+60°+60°=360°
120°+60°+60°+60°+60°=360°
(2)正三角形和正六边形的组合
150°+150°+60°=360°
(3)正三角形和正十二边形组合
(4)正方形和正八边形组合
135°+135°+90°=360°
144°+108°+108°=360 °
(5)正五边形和正十边形的组合
正多边形的边数n 3 4 5 6 7 8 9 10 12
每个内角的度数 60 90 108 120 135 140 140 144 150
解不定方程其中是正多边形每个内角的度数,是对应正多边形的个数.
数学道理
用三种正多边形镶嵌,哪些能镶嵌成一个平面?
问题4
(1)正三角形、正方形和正六边形的组合
120°+90°+90°+60°=360 °
(2)正方形、正六边形和正十二边形的组合
150°+120°+90°=360 °
正多边形的边数n 3 4 5 6 7 8 9 10 12
每个内角的度数 60 90 108 120 135 140 140 144 150
解不定方程其中是正多边形每个内角的度数,是对应正多边形的个数.
数学道理
再见
