人教版八年级数学上册 11.1.2 三角形的高、中线与角平分线教学课件(共17张ppt)
文档属性
| 名称 | 人教版八年级数学上册 11.1.2 三角形的高、中线与角平分线教学课件(共17张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 481.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-20 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
第十一章 三角形
11.1 与三角形有关的线段
11.1.2 三角形的高、中线与角平分线
数一数,图中共有多少个三角形 请将它们全部用符号表示出来.
A
C
B
D
E
图中共有 5 个三角形:
△ABC,△ABD,△ACD,△ADE,△CDE.
一、复习回顾
利用长为 3,5,6,9 的四条线段可以组成几个三角形 为什么
可以组成 2 个三角形.
从四条线段中任选三条组成三角形,共有四种选法:
①3,5,6,②3,5,9,③3,6,9,④5,6,9.
其中,满足“三角形两边之和大于第三边”的只有第①,④这两组.
利用△ABC 的一条边长为 4 cm,面积是 24 cm2这两个条件,你能求出这条边上的高吗
这条边上的高是 12 cm.
一、复习回顾
三角形的高
如右图,从△ABC 的顶点向它所对的边BC 所在直线画垂线,垂足为 D,所得线段 AD 叫做△ABC 的边 BC 上的高.
从三角形一个顶点向它的对边所在的直线做垂线,顶点和垂足间的线段叫做三角形的高线,简称三角形的高.
A
B
C
D
(1)什么是三角形的高?(定义)
二、合作交流,探究新知
三角形的高
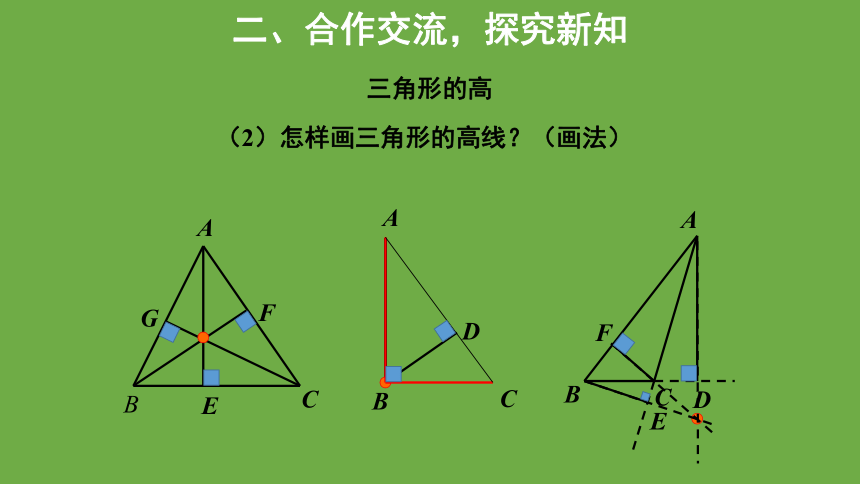
(2)怎样画三角形的高线?(画法)
A
B
C
E
F
G
A
B
D
A
B
C
E
D
F
C
二、合作交流,探究新知
三角形的高
①锐角三角形,直角三角形,钝角三角形都有高线,三角形的三条高线所在直线相交于一点.
②锐角三角形的高线交于三角形的内部一点.
直角三角形高线交于直角顶点.
钝角三角形高线交于三角形外部一点.
③三角形的高是线段,而垂线是直线.
二、合作交流,探究新知
三角形的中线
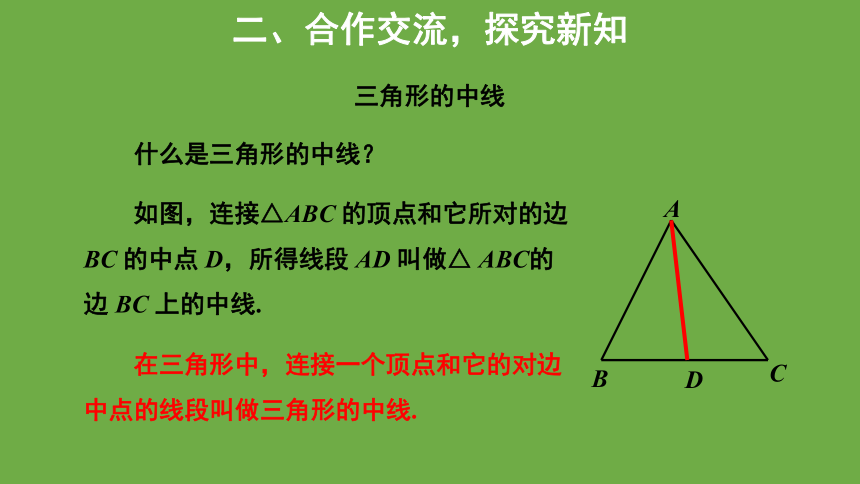
什么是三角形的中线?
如图,连接△ABC 的顶点和它所对的边BC 的中点 D,所得线段 AD 叫做△ ABC的边 BC 上的中线.
在三角形中,连接一个顶点和它的对边中点的线段叫做三角形的中线.
A
B
C
D
二、合作交流,探究新知
三角形的角平分线
画∠A 的平分线 AD,交∠A 所对的边 BC于点 D,线段 AD 叫做ΔABC 的角平分线.
A
C
B
D
●
●
F
E
●
●
●
●
画出ΔABC 的另外两条角平分线;
观察三条角平分线,说说你的发现.
三角形的三条角平分线在三角形的内部交于一点.
二、合作交流,探究新知
如图所示,在△ABC中,AD 是△ABC 的中线,AE 是△ABC 的高. 试判断△ABD 和△ACD 的面积有什么关系 为什么
解:∵AD 是△ABC的中线,
∴BD = CD.
∵AE 既是△ABD 的高,也是△ACD 的高,
∴△ABD 和△ACD 的面积相等.
三、运用新知
如图,已知:△ABC 中,BD,CE 分别是△ABC 的两条角平分线,相交于点 O.
(1)当∠ABC = 60°,∠ACB = 80°时,求∠BOC 的度数.
解: ∵ BD,CE 分别是△ABC 的角平分线
三、运用新知
(2)当∠A = 40°时,求∠BOC 的度数.
解: ∵BD,CE 分别是△ABC 的角平分线
三、运用新知
如图,已知:△ABC 中,BD,CE 分别是△ABC 的两条角平分线,相交于点 O.
(3)当∠A= x°时,求∠BOC 的度数(用含 x 的式子表示).
解:∵BD,CE 分别是△ABC 的角平分线
三、运用新知
如图,已知:△ABC 中,BD,CE 分别是△ABC 的两条角平分线,相交于点 O.
1. 如图,已知AD,BE,CF都是△ABC的三条中线,则AE= = ,BC=2 ,AF= .
CE;AC;BD 或 CD;BF.
四、巩固新知
2. 如图,已知 AD,BE,CF 都是△ABC 的三条角平分线.
则∠BAD = ,∠ACF= = ,∠ABC=2 .
∠BAC;∠FCB,∠ACB;∠CBE 或∠ABE.
四、巩固新知
3. 如图,△ABC 中,AC = 12 cm,BC = 18 cm,△ABC 的高 AD 与 BE 的比是多少
解:由三角形的面积公式得
S△ABC = BC×AD = AC×BE,
所以有 ×18×AD = ×12×BE,
解得 AD∶BE = 2∶3.
四、巩固新知
三角形的角平分线、中线、高线的比较
相同点:
1. 都是线段.
2. 都从顶点画出.
3. 所在直线都相交于一点.
不同点:
1. 角平分线反映的是角的相等关系.
2. 中线反映的是线段的相等关系.
3. 高线反映的是它和对边或对边所在直线的垂直关系.
五、归纳小结
再 见
第十一章 三角形
11.1 与三角形有关的线段
11.1.2 三角形的高、中线与角平分线
数一数,图中共有多少个三角形 请将它们全部用符号表示出来.
A
C
B
D
E
图中共有 5 个三角形:
△ABC,△ABD,△ACD,△ADE,△CDE.
一、复习回顾
利用长为 3,5,6,9 的四条线段可以组成几个三角形 为什么
可以组成 2 个三角形.
从四条线段中任选三条组成三角形,共有四种选法:
①3,5,6,②3,5,9,③3,6,9,④5,6,9.
其中,满足“三角形两边之和大于第三边”的只有第①,④这两组.
利用△ABC 的一条边长为 4 cm,面积是 24 cm2这两个条件,你能求出这条边上的高吗
这条边上的高是 12 cm.
一、复习回顾
三角形的高
如右图,从△ABC 的顶点向它所对的边BC 所在直线画垂线,垂足为 D,所得线段 AD 叫做△ABC 的边 BC 上的高.
从三角形一个顶点向它的对边所在的直线做垂线,顶点和垂足间的线段叫做三角形的高线,简称三角形的高.
A
B
C
D
(1)什么是三角形的高?(定义)
二、合作交流,探究新知
三角形的高
(2)怎样画三角形的高线?(画法)
A
B
C
E
F
G
A
B
D
A
B
C
E
D
F
C
二、合作交流,探究新知
三角形的高
①锐角三角形,直角三角形,钝角三角形都有高线,三角形的三条高线所在直线相交于一点.
②锐角三角形的高线交于三角形的内部一点.
直角三角形高线交于直角顶点.
钝角三角形高线交于三角形外部一点.
③三角形的高是线段,而垂线是直线.
二、合作交流,探究新知
三角形的中线
什么是三角形的中线?
如图,连接△ABC 的顶点和它所对的边BC 的中点 D,所得线段 AD 叫做△ ABC的边 BC 上的中线.
在三角形中,连接一个顶点和它的对边中点的线段叫做三角形的中线.
A
B
C
D
二、合作交流,探究新知
三角形的角平分线
画∠A 的平分线 AD,交∠A 所对的边 BC于点 D,线段 AD 叫做ΔABC 的角平分线.
A
C
B
D
●
●
F
E
●
●
●
●
画出ΔABC 的另外两条角平分线;
观察三条角平分线,说说你的发现.
三角形的三条角平分线在三角形的内部交于一点.
二、合作交流,探究新知
如图所示,在△ABC中,AD 是△ABC 的中线,AE 是△ABC 的高. 试判断△ABD 和△ACD 的面积有什么关系 为什么
解:∵AD 是△ABC的中线,
∴BD = CD.
∵AE 既是△ABD 的高,也是△ACD 的高,
∴△ABD 和△ACD 的面积相等.
三、运用新知
如图,已知:△ABC 中,BD,CE 分别是△ABC 的两条角平分线,相交于点 O.
(1)当∠ABC = 60°,∠ACB = 80°时,求∠BOC 的度数.
解: ∵ BD,CE 分别是△ABC 的角平分线
三、运用新知
(2)当∠A = 40°时,求∠BOC 的度数.
解: ∵BD,CE 分别是△ABC 的角平分线
三、运用新知
如图,已知:△ABC 中,BD,CE 分别是△ABC 的两条角平分线,相交于点 O.
(3)当∠A= x°时,求∠BOC 的度数(用含 x 的式子表示).
解:∵BD,CE 分别是△ABC 的角平分线
三、运用新知
如图,已知:△ABC 中,BD,CE 分别是△ABC 的两条角平分线,相交于点 O.
1. 如图,已知AD,BE,CF都是△ABC的三条中线,则AE= = ,BC=2 ,AF= .
CE;AC;BD 或 CD;BF.
四、巩固新知
2. 如图,已知 AD,BE,CF 都是△ABC 的三条角平分线.
则∠BAD = ,∠ACF= = ,∠ABC=2 .
∠BAC;∠FCB,∠ACB;∠CBE 或∠ABE.
四、巩固新知
3. 如图,△ABC 中,AC = 12 cm,BC = 18 cm,△ABC 的高 AD 与 BE 的比是多少
解:由三角形的面积公式得
S△ABC = BC×AD = AC×BE,
所以有 ×18×AD = ×12×BE,
解得 AD∶BE = 2∶3.
四、巩固新知
三角形的角平分线、中线、高线的比较
相同点:
1. 都是线段.
2. 都从顶点画出.
3. 所在直线都相交于一点.
不同点:
1. 角平分线反映的是角的相等关系.
2. 中线反映的是线段的相等关系.
3. 高线反映的是它和对边或对边所在直线的垂直关系.
五、归纳小结
再 见
