切线长定理

课题 切线长定理 课型 新授 教案序号
教学环境和教学资源 教室、多媒体、笔记本、练习本
学习目标
1. 理解切线长的定义；2. 探索证明切线长定理，并能灵活运用切线长定理解题。3.体会运用数形结合，转化等数学思想。
教材处理 学生活动设计
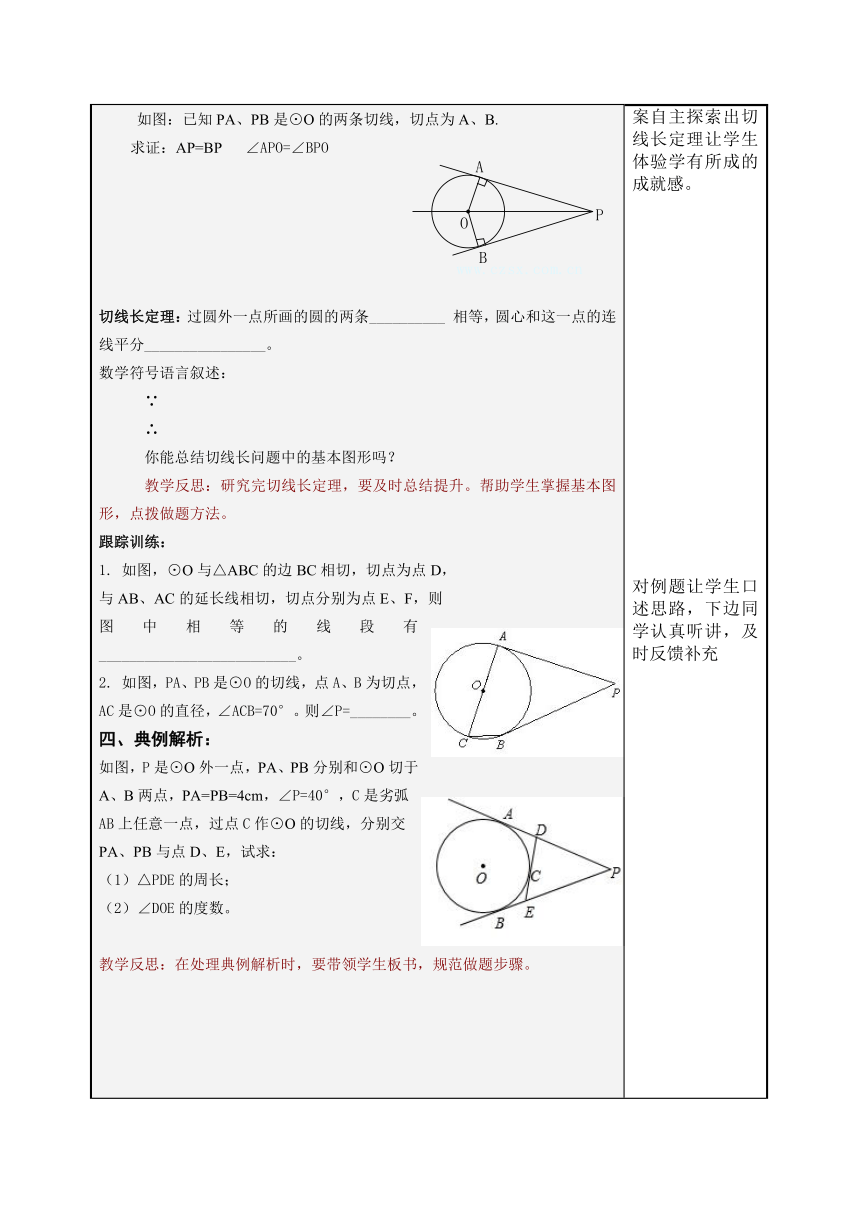
一、知识准备：1. 直线与圆的位置关系有哪些？怎样判定？2. 切线的判定和性质是什么？二、课前预习：（一）切线长的定义：如下图，过⊙O外一点P，作出⊙O的所有切线。 P切线长概念：过圆外一点，可以作圆的______条切线，这点与其中一个切点之间的____的长，叫做这点到圆的切线长。（二） 探究切线与切线长的区别：区别切线切线长跟踪训练：判断：1. 圆的切线长就圆的切线的长度。（ ）2. 过任意一点总可以作圆的两条切线。（ ）三、探究新知探究切线长定理：如图：已知PA、PB是⊙O的两条切线，切点为A、B.求证：AP=BP ∠APO=∠BPO 切线长定理：过圆外一点所画的圆的两条__________ 相等，圆心和这一点的连线平分________________。 数学符号语言叙述： ∵∴你能总结切线长问题中的基本图形吗？教学反思：研究完切线长定理，要及时总结提升。帮助学生掌握基本图形，点拨做题方法。跟踪训练：1. 如图，⊙O与△ABC的边BC相切，切点为点D，与AB、AC的延长线相切，切点分别为点E、F，则图中相等的线段有__________________________。2. 如图，PA、PB是⊙O的切线，点A、B为切点，AC是⊙O的直径，∠ACB=70°。则∠P=________。四、典例解析：如图，P是⊙O外一点，PA、PB分别和⊙ ( http: / / www.21cnjy.com )O切于A、B两点，PA=PB=4cm，∠P=40°，C是劣弧AB上任意一点，过点C作⊙O的切线，分别交PA、PB与点D、E，试求：（1）△PDE的周长；（2）∠DOE的度数。教学反思：在处理典例解析时，要带领学生板书，规范做题步骤。直击中考：如图，PC是⊙O的切线，C是切点 ( http: / / www.21cnjy.com )，PO交⊙O于点 A，过点A的切线交 PC于点D，CD∶DP = 1∶2，AD=2cm，求⊙O的半径。五、课堂小结：畅所欲言，查漏补缺 学习目标回顾：六、当堂检测：1. 如图， P是⊙O外一点，PA、PB ( http: / / www.21cnjy.com )分别与⊙O相切于点A、B，C是AB上任一点，过C作⊙O的切线分别交 PA、PB 于点 D、E。若△PDE的周长为12，则PA=_______ 。教学反思：本题与典例解析很相似，可以变成一道填空题，以节省时间。2. 如图，PA、PB是⊙O的切线，A、B为切点，∠OAB=30°。（1）求∠APB的度数；（2）当OA=3时，求AP的长。七、课后提升：1．如图所示，PA、PB是⊙O的两条切线，A、B为切点，求证：∠ABO=∠APB。2．如图，EB、EC是⊙O的两条切线，B、C是切点，A、D是⊙O上两点，如果∠E=46°，∠DCF=32°，求∠A的度数。3.如图所示PA、PB分别切圆O于A、B，并与圆O的切线分别相交于C、D，已知PA=7cm，(1)求△PCD的周长．(2)如果∠P=46°,求∠COD的度数4. 如图，直线、分别切圆O于A、B，且∥，切圆O于E，交、于点C、D，求证：∠COD=90°变式：若OC=6，OD=8，则CD= 。 学生活动设计一：知识回顾组内交流复习内容：选好代表做展示准备。学生活动设计二：组内交流预习内容，代表展示。学生活动设计三：探索新知，学生根据学案自主探索出切线长定理让学生体验学有所成的成就感。对例题让学生口述思路，下边同学认真听讲，及时反馈补充学生活动设计四：中考链接1.通过联系本节与中考的关系，让学生明确中考的动向。学生活动设计五：小结本节你学了哪些知识本课渗透了哪些数学思想？本节课的学习目标你完成了多少？学生活动设计六：当堂检测第一题学生独立完成第二题找一学生板演。七：课后提升由学生课后完成。
教学反思 1.在得出切线长定理后并用符号语言表示后，直接进行跟踪训练，再进行跟踪训练2.典例解析要注意知识应用的规范性。3.要渗透做题思想指导：遇切点连圆心。4.要关注后半部分学生，掌握整体学情。如：有针对性找谁回答问题。5.注意课堂时间安排。6.通解决问题时要留给学生足够的思考时间，足够的做的时间，足够的改的时间，要落实的扎扎实实。
·
O