2014-2015学年第一学期河北省保定市八校联合体高二期中联考(文)
文档属性
| 名称 | 2014-2015学年第一学期河北省保定市八校联合体高二期中联考(文) |  | |
| 格式 | zip | ||
| 文件大小 | 165.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-02 22:13:40 | ||
图片预览



文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
2014-2015学年第一学期河北省保定市八校联合体高二期中联考
高二数学(文科)
(满分150分,考试时间:120分钟)
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟,注意事项:
1.第Ⅰ卷的答案填在答题卷方框里,第Ⅱ卷的答案或解答过程写在答题卷指定处,写在试题卷上的无效。
2.答题前,考生务必将自己的“姓名”、“班级”、和“考号”写在答题卷上。
3.考试结束,只交答题卷。
第Ⅰ卷(选择题共60分)
1、 选择题:(本大题共12题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)【来源:21·世纪·教育·网】
1.命题“若,则”的否命题是( )
A.若,则 B.若,则
C.若,则 D.若,则
2.下列说法正确的是( )
A.命题“若”,则“”的逆命题是真命题
B.命题“若”,的否定是“”
C.命题“p或q”,则命题“p”和命题“q”均为真命题
D.已知,则“x>1”是“x>2”的充分不必要条件
3.函数的图象与直线相切,则a等于( )21·cn·jy·com
A B C D 121·世纪*教育网
4.如果双曲线的两个焦点分别为、,一条渐近线方程为,那么它的两条准线间的距离是( )
A、 B、2 C、4 D、1
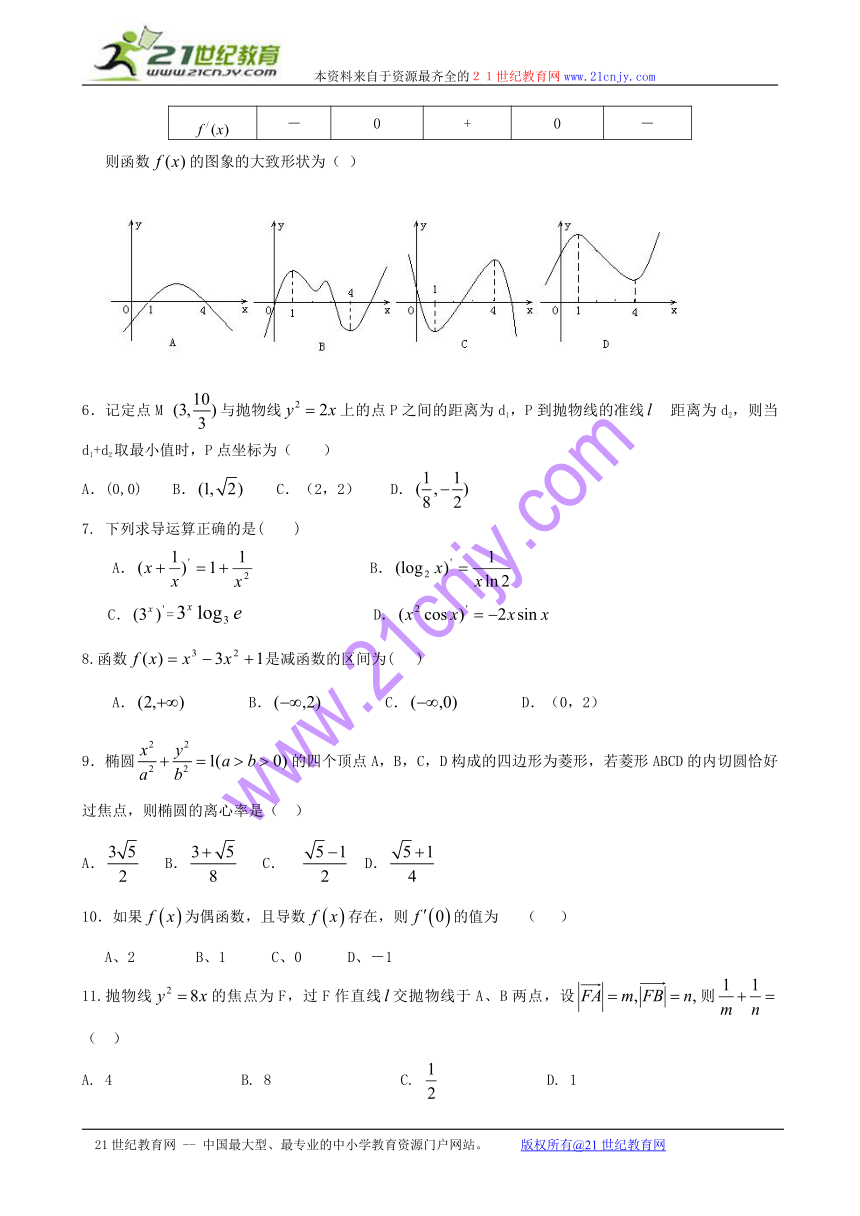
5.当在上变化时,导函数的符号变化如下表:
1 (1,4) 4
- 0 + 0 -
则函数的图象的大致形状为( )
6.记定点M 与抛物线上的点P之间的距离为d1,P到抛物线的准线 距离为d2,则当d1+d2取最小值时,P点坐标为( )21世纪教育网版权所有
A.(0,0) B. C.(2,2) D.
7. 下列求导运算正确的是( )
A. B.
C.= D.
8.函数是减函数的区间为( )
A. B. C. D.(0,2)
9.椭圆的四个顶点A,B,C,D构成的四边形为菱形,若菱形ABCD的内切圆恰好过焦点,则椭圆的离心率是( )www-2-1-cnjy-com
A. B. C. D.
10.如果为偶函数,且导数存在,则的值为 ( )
A、2 B、1 C、0 D、-1
11.抛物线的焦点为F,过F作直线交抛物线于A、B两点,设则 ( )
A. 4 B. 8 C. D. 12-1-c-n-j-y
12、右上图是函数y=f(x)的导函数y=f′(x)的图象,则下面判断正确的是 ( )
A.在区间(-3,1)内f(x)是增函数 B.在x=2时f(x)取得极大值
C.在(4,5)内f(x)是增函数 D.在x=2时f(x)取到极小值
第II卷(非选择题共90分)
二、填空题:(本大题共4小题,每小题5分,满分20分.)
13.已知命题与命题
都是真命题, 则实数的取值范围是 .
14.在平面直角坐标系中,已知△ABC的顶点A(-4,0),C(4,0)且顶点B在椭圆上,则____________。 21*cnjy*com
15.曲线在点处的切线方程为 .
16.给出下列命题:
①,使得; ②曲线表示双曲线;
③的递减区间为 ④对,使得 . 其中真命题为 (填上序号)21教育网
三、解答题:(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)
17.(本大题满分10分)
已知命题p:方程表示焦点在y轴上的椭圆;
命题q:双曲线的离心率,若p、q有且只有一个为真,求m的取值范围.
18.(本题满分12分)已知椭圆(a>b>0)
(1)当椭圆的离心率,一条准线方程为x=4 时,求椭圆方程;
(2)设是椭圆上一点,在(1)的条件下,求的最大值及相应的P点坐标。
(3)过B(0,-b)作椭圆(a>b>0)的弦,若弦长的最大值不是2b,求椭圆离心率的取值范围。
19. (本题满分12分)设.若在 存在单调增区间,求a的取值范围.
20.(本题满分12分)
已知:如图,圆O:交轴于A,B两点,曲线C是以AB为长轴,离心率为的椭圆,其左焦点为F,若P是圆O上一点,连结PF,过原点O作直线PF的垂线交椭圆的左准线于点Q。
(1)求椭圆的标准方程;
(2)若点P的坐标为(1,1),
①求线段PQ的长;
②求证:直线PQ与圆O相切;
21.(本小题满分12分)
已知函数.
(1)当时,求函数的单调区间;
(2) 当a >0时,求函数在上最小值.
22.(本小题满分12分)
已知一条抛物线和一个椭圆都经过点M(1,2),它们在x轴上具有相同的焦点F1,且两者的对称轴都是坐标轴,抛物线的顶点在坐标原点。www.21-cn-jy.com
(1) 求抛物线的方程和椭圆方程;
(2) 假设椭圆的另一个焦点是F2,经过F2的直线与抛物线交于P,Q两点,且满足,求m的取值范围。
高二数学试卷答案
一、选择题 BBBBC CAADC CC
二、填空题
13. ;14.;;15. ;16.①③
三、解答题:
17.解:将方程改写为,
只有当即时,方程表示的曲线是焦点在y轴上的椭圆,所以命题p等价于;………………………………………………………………………4分
因为双曲线的离心率,
所以,且1,解得,…………………………………6分
所以命题q等价于; ……………………………………………………8分
若p真q假,则;
若p假q真,则
综上:的取值范围为………………………………………………………12分
18.解:(1),椭圆方程为……………3分
(2)因为在椭圆上,所以可设,
则,
,此时,
相应的P点坐标为。 …………………………………6分
(3)设弦为BP,其中P(x,y),
=,
因为BP的最大值不是2b,又, …………………………………8分
所以f(y)不是在y=b时取最大值,而是在对称轴处取最大值,
所以,所以,解得离心率…………………………………12分
19. 解:(1)由……………………………2分
当 令
所以,当上存在单调递增区间. ……………………………4分
(2)令
所以上单调递减,在上单调递增 ………………8分
当在[1,4]上的最大值为
又所以在[1,4]上的最小值为
…………………………………10分
得,从而在[1,4]上的最大值为… ……………12分
20.(本题满分12分)
解:(1)设椭圆的标准方程为
因为圆O: 交轴于A、B两点,所以AB=
即 ………………………………………………………………1分
而椭圆的离心率为,所以,故… ………………………………………2分
因此椭圆的标准方程为 ………………………………………………3分
(2)①由(1)知椭圆的左焦点F(—1,0),而点P(1,1)
所以直线PF的方程为 ………………………………………………4分
直线QO的方程为 …………………………………………………………6分
而椭圆的左准线方程为
所以点Q的坐标为(—2,4)
因此 ……………………………………………………………………8分
②证明:直线PQ的方程为:,即……………………10分
而点O到直线PQ的距离为
所以直线PQ与圆O相切 …………………………………………………………12分
21.解: (Ⅰ) (), …………………………………1分
①由,得 ……………… …………………2分
②由,得 ……………………………3分
故函数的单调递增区间为,单调减区间是. ………………4分
(Ⅱ)①当,即时,函数在区间[1,2]上是减函数,
∴的最小值是. ………………6分
②当,即时,函数在区间[1,2]上是增函数,
∴的最小值是. ………………8分
③当,即时,函数在上是增函数,在是减函数.
又,
∴当时,最小值是;
当时,最小值为. ………………10分
综上可知,当时, 函数的最小值是;当时,函数的最小值是. ………………12分21cnjy.com
22.解:(1)由题意可设抛物线方程为,
把M点代入方程得:抛物线方程为………………………………………………..2分
所以F1(1,0),且经过点M,故设椭圆方程为,联立方程得
解得,
故椭圆方程为………………………………………………………………..6分
(2)易知F2(-1,0),设直线的方程为y=k(x+1),联立方程得,消去y得,因为直线与抛物线相交于P、Q两点,2·1·c·n·j·y
所以,解得-1设P()Q(),则,
由得,所以,
∵P、Q为不同的两点,∴,即,∴
解得,∴………………………………………………..10分
即,∵,∴,即
所以m>0且……………………………………………………………………………….12分
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
2014-2015学年第一学期河北省保定市八校联合体高二期中联考
高二数学(文科)
(满分150分,考试时间:120分钟)
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟,注意事项:
1.第Ⅰ卷的答案填在答题卷方框里,第Ⅱ卷的答案或解答过程写在答题卷指定处,写在试题卷上的无效。
2.答题前,考生务必将自己的“姓名”、“班级”、和“考号”写在答题卷上。
3.考试结束,只交答题卷。
第Ⅰ卷(选择题共60分)
1、 选择题:(本大题共12题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)【来源:21·世纪·教育·网】
1.命题“若,则”的否命题是( )
A.若,则 B.若,则
C.若,则 D.若,则
2.下列说法正确的是( )
A.命题“若”,则“”的逆命题是真命题
B.命题“若”,的否定是“”
C.命题“p或q”,则命题“p”和命题“q”均为真命题
D.已知,则“x>1”是“x>2”的充分不必要条件
3.函数的图象与直线相切,则a等于( )21·cn·jy·com
A B C D 121·世纪*教育网
4.如果双曲线的两个焦点分别为、,一条渐近线方程为,那么它的两条准线间的距离是( )
A、 B、2 C、4 D、1
5.当在上变化时,导函数的符号变化如下表:
1 (1,4) 4
- 0 + 0 -
则函数的图象的大致形状为( )
6.记定点M 与抛物线上的点P之间的距离为d1,P到抛物线的准线 距离为d2,则当d1+d2取最小值时,P点坐标为( )21世纪教育网版权所有
A.(0,0) B. C.(2,2) D.
7. 下列求导运算正确的是( )
A. B.
C.= D.
8.函数是减函数的区间为( )
A. B. C. D.(0,2)
9.椭圆的四个顶点A,B,C,D构成的四边形为菱形,若菱形ABCD的内切圆恰好过焦点,则椭圆的离心率是( )www-2-1-cnjy-com
A. B. C. D.
10.如果为偶函数,且导数存在,则的值为 ( )
A、2 B、1 C、0 D、-1
11.抛物线的焦点为F,过F作直线交抛物线于A、B两点,设则 ( )
A. 4 B. 8 C. D. 12-1-c-n-j-y
12、右上图是函数y=f(x)的导函数y=f′(x)的图象,则下面判断正确的是 ( )
A.在区间(-3,1)内f(x)是增函数 B.在x=2时f(x)取得极大值
C.在(4,5)内f(x)是增函数 D.在x=2时f(x)取到极小值
第II卷(非选择题共90分)
二、填空题:(本大题共4小题,每小题5分,满分20分.)
13.已知命题与命题
都是真命题, 则实数的取值范围是 .
14.在平面直角坐标系中,已知△ABC的顶点A(-4,0),C(4,0)且顶点B在椭圆上,则____________。 21*cnjy*com
15.曲线在点处的切线方程为 .
16.给出下列命题:
①,使得; ②曲线表示双曲线;
③的递减区间为 ④对,使得 . 其中真命题为 (填上序号)21教育网
三、解答题:(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)
17.(本大题满分10分)
已知命题p:方程表示焦点在y轴上的椭圆;
命题q:双曲线的离心率,若p、q有且只有一个为真,求m的取值范围.
18.(本题满分12分)已知椭圆(a>b>0)
(1)当椭圆的离心率,一条准线方程为x=4 时,求椭圆方程;
(2)设是椭圆上一点,在(1)的条件下,求的最大值及相应的P点坐标。
(3)过B(0,-b)作椭圆(a>b>0)的弦,若弦长的最大值不是2b,求椭圆离心率的取值范围。
19. (本题满分12分)设.若在 存在单调增区间,求a的取值范围.
20.(本题满分12分)
已知:如图,圆O:交轴于A,B两点,曲线C是以AB为长轴,离心率为的椭圆,其左焦点为F,若P是圆O上一点,连结PF,过原点O作直线PF的垂线交椭圆的左准线于点Q。
(1)求椭圆的标准方程;
(2)若点P的坐标为(1,1),
①求线段PQ的长;
②求证:直线PQ与圆O相切;
21.(本小题满分12分)
已知函数.
(1)当时,求函数的单调区间;
(2) 当a >0时,求函数在上最小值.
22.(本小题满分12分)
已知一条抛物线和一个椭圆都经过点M(1,2),它们在x轴上具有相同的焦点F1,且两者的对称轴都是坐标轴,抛物线的顶点在坐标原点。www.21-cn-jy.com
(1) 求抛物线的方程和椭圆方程;
(2) 假设椭圆的另一个焦点是F2,经过F2的直线与抛物线交于P,Q两点,且满足,求m的取值范围。
高二数学试卷答案
一、选择题 BBBBC CAADC CC
二、填空题
13. ;14.;;15. ;16.①③
三、解答题:
17.解:将方程改写为,
只有当即时,方程表示的曲线是焦点在y轴上的椭圆,所以命题p等价于;………………………………………………………………………4分
因为双曲线的离心率,
所以,且1,解得,…………………………………6分
所以命题q等价于; ……………………………………………………8分
若p真q假,则;
若p假q真,则
综上:的取值范围为………………………………………………………12分
18.解:(1),椭圆方程为……………3分
(2)因为在椭圆上,所以可设,
则,
,此时,
相应的P点坐标为。 …………………………………6分
(3)设弦为BP,其中P(x,y),
=,
因为BP的最大值不是2b,又, …………………………………8分
所以f(y)不是在y=b时取最大值,而是在对称轴处取最大值,
所以,所以,解得离心率…………………………………12分
19. 解:(1)由……………………………2分
当 令
所以,当上存在单调递增区间. ……………………………4分
(2)令
所以上单调递减,在上单调递增 ………………8分
当在[1,4]上的最大值为
又所以在[1,4]上的最小值为
…………………………………10分
得,从而在[1,4]上的最大值为… ……………12分
20.(本题满分12分)
解:(1)设椭圆的标准方程为
因为圆O: 交轴于A、B两点,所以AB=
即 ………………………………………………………………1分
而椭圆的离心率为,所以,故… ………………………………………2分
因此椭圆的标准方程为 ………………………………………………3分
(2)①由(1)知椭圆的左焦点F(—1,0),而点P(1,1)
所以直线PF的方程为 ………………………………………………4分
直线QO的方程为 …………………………………………………………6分
而椭圆的左准线方程为
所以点Q的坐标为(—2,4)
因此 ……………………………………………………………………8分
②证明:直线PQ的方程为:,即……………………10分
而点O到直线PQ的距离为
所以直线PQ与圆O相切 …………………………………………………………12分
21.解: (Ⅰ) (), …………………………………1分
①由,得 ……………… …………………2分
②由,得 ……………………………3分
故函数的单调递增区间为,单调减区间是. ………………4分
(Ⅱ)①当,即时,函数在区间[1,2]上是减函数,
∴的最小值是. ………………6分
②当,即时,函数在区间[1,2]上是增函数,
∴的最小值是. ………………8分
③当,即时,函数在上是增函数,在是减函数.
又,
∴当时,最小值是;
当时,最小值为. ………………10分
综上可知,当时, 函数的最小值是;当时,函数的最小值是. ………………12分21cnjy.com
22.解:(1)由题意可设抛物线方程为,
把M点代入方程得:抛物线方程为………………………………………………..2分
所以F1(1,0),且经过点M,故设椭圆方程为,联立方程得
解得,
故椭圆方程为………………………………………………………………..6分
(2)易知F2(-1,0),设直线的方程为y=k(x+1),联立方程得,消去y得,因为直线与抛物线相交于P、Q两点,2·1·c·n·j·y
所以,解得-1
由得,所以,
∵P、Q为不同的两点,∴,即,∴
解得,∴………………………………………………..10分
即,∵,∴,即
所以m>0且……………………………………………………………………………….12分
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
