2014-2015学年第一学期河北省保定市八校联合体高三期中联考(文科)
文档属性
| 名称 | 2014-2015学年第一学期河北省保定市八校联合体高三期中联考(文科) |  | |
| 格式 | zip | ||
| 文件大小 | 192.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-02 22:19:02 | ||
图片预览



文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
2014-2015学年第一学期河北省保定市八校联合体高三期中联考
高三数学(文科)
(满分150分,考试时间:120分钟)
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟,注意事项:
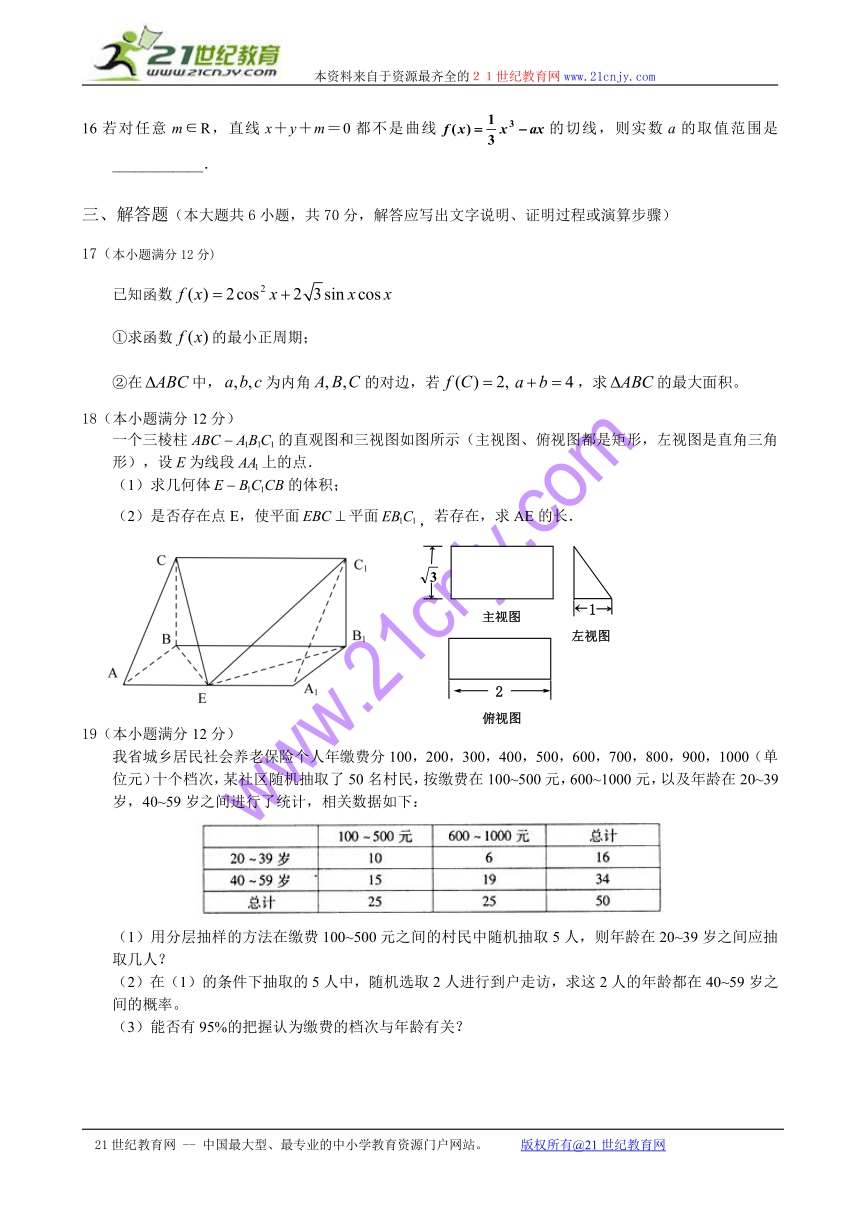
1.第Ⅰ卷的答案填在答题卷方框里,第Ⅱ卷的答案或解答过程写在答题卷指定处,写在试题卷上的无效。
2.答题前,考生务必将自己的“姓名”、“班级”、和“考号”写在答题卷上。
3.考试结束,只交答题卷。
第Ⅰ卷(选择题共60分)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的,把答案填涂在答题卷相应位置上)21世纪教育网版权所有
1.已知,若共线,则实数x=
A. B. C.1 D.2
2.命题:“”的否定为
A. B.
C. D.
3.把函数的图象向左平移个单位长度后,所得到的图象关于y轴对称,则m的最小值是
A. B. C. D.
4数f (x)=+3x的零点个数是
(A) 0 (B) 1 (C) 2 (D) 321教育网
5已知直线l∥平面α,P∈α,那么过点P且平行于直线l的直线
(A) 只有一条,不在平面α内
(B) 有无数条,不一定在平面α内
(C) 只有一条,且在平面α内
(D) 有无数条,一定在平面α内
6 ( http: / / www. / )为非零向量“函数为偶函数”是“ ( http: / / www. / )”的
A.充分不必要条件 ( http: / / www. / ) B. 必要不充分条件
C.充要条件 D. 既不充分又不必要条件
7某几何体的三视图 (单位:cm) 如图所示,则此几何体的体积是
(A) 36 cm3 (B) 48 cm3
(C) 60 cm3 (D) 72 cm3
8函数,则y的取值范围是
A. B. C. D.
9已知 ( http: / / www. / )是内的一点,且 ( http: / / www. / ),则 ( http: / / www. / )、和 ( http: / / www. / )的面积分别为;则 ( http: / / www. / )的最小值为
A.20 B.19 C.16 D.1821cnjy.com
10.列是首项为1,公比为的等比数列,则等于
A.-32 B.32 C.-64 D.64
11.外接圆的圆心为,半径为,且,则向量 在方向上的投影为
A. B. C. D.
12.已知数列满足:,用[x]表示不超过x的最大整数,则
的值等于
A.0 B.1 C.2 D.3
第II卷(非选择题共90分)
二、填空题(本大题共4小题,每小题5分,共20分,把答案填在答题卷相应位置上)
13.=
14已知 ( http: / / www. / )为等差数列,, ( http: / / www. / )为其前n项和,则使达到最大值的n等于__ ( http: / / www. / )_________.
15某圆锥体的底面半径,沿圆锥体的母线把侧面展开后可得到圆心角为的扇形,则该圆锥体的体积是 . www.21-cn-jy.com
16若对任意m∈R,直线x+y+m=0都不是曲线的切线,则实数a的取值范围是____________. 2·1·c·n·j·y
三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)
17(本小题满分12分)
已知函数
①求函数 ( http: / / www. / )的最小正周期;
②在中, ( http: / / www. / )为内角的对边,若 ( http: / / www. / ),求 ( http: / / www. / )的最大面积。
18(本小题满分12分)
一个三棱柱的直观图和三视图如图所示(主视图、俯视图都是矩形,左视图是直角三角形),设为线段上的点.【来源:21·世纪·教育·网】
(1)求几何体的体积;
(2)是否存在点E,使平面平面,若存在,求AE的长.
19(本小题满分12分)
我省城乡居民社会养老保险个人年缴费分1 ( http: / / www.21cnjy.com )00,200,300,400,500,600,700,800,900,1000(单位元)十个档次,某社区随机抽取了50名村民,按缴费在100~500元,600~1000元,以及年龄在20~39岁,40~59岁之间进行了统计,相关数据如下:21·cn·jy·com
( http: / / www.21cnjy.com )
(1)用分层抽样的方法在缴费100~500元之间的村民中随机抽取5人,则年龄在20~39岁之间应抽取几人?21·世纪*教育网
(2)在(1)的条件下抽取的5人中,随机选取2人进行到户走访,求这2人的年龄都在40~59岁之间的概率。www-2-1-cnjy-com
(3)能否有95%的把握认为缴费的档次与年龄有关?
( http: / / www.21cnjy.com )
20.小题满分12分)
等差数列的前n项的和为 ( http: / / www. / ),且
(1)求 ( http: / / www. / )的通项公式;
(2)若数列满足 ( http: / / www. / ),且设数列 ( http: / / www. / )的前n项和为.
求证: ( http: / / www. / ).
21(本题满分12分)
椭圆:的右焦点,离心率为,已知点坐标是,点是椭圆上的动点.
(1)求椭圆的方程;
(2)求的最大值及此时的点坐标.
22. (本小题满分12分)设函数
(1)当曲线处的切线方程
(2)求函数的单调区间与极值;
(3)已知函数有三个互不相同的零点0,,且。若对任意的,恒成立,求m的取值范围。
文科数学参考答案
一、选择题 BBCBC DCBCB CB
二、填空题
13.;14.5;15.;16.;
三 ( http: / / www. / )、解答题
17.解:①由已知
( http: / / www. / ) ……………………………… 6分
②由①知,即 ( http: / / www. / )
又∴ ( http: / / www. / )
当且仅当 ( http: / / www. / )时, …………………………………………12分
18.解:(Ⅰ)由题可知,三棱柱为直三棱柱,底面,
且底面是直角三角形, ,,…………2分
三棱柱的体积…………4分
(Ⅱ)三棱柱为直三棱柱,底面,
,,又,
, ………………6分
又平面, …………………9分
由,,,得平面,
又平面,平面平面. ……………12分
19(Ⅰ)设抽取人,则,,所以在20~39岁之间应抽取2人.
…………………3分
(Ⅱ)记在缴费100~500元之间抽取的5人中,年龄20~39的两人为,
年龄40~59 岁的三人为, 所以随机抽取2人的所有情况有:
10种,其中年龄都在40~59岁之间有3种,故……………………8分
(III),因为,所以没有的把握认为缴费档次和年龄有关. ………………………………………………12分
20. 解:1) ( http: / / www. / ), 由
解得 ( http: / / www. / ) 又
所以 ( http: / / www. / ) ……………………………………………………… …………………4
2)
( http: / / www. / )
。。。。。。
( http: / / www. / )
叠加得
所以 ( http: / / www. / )………………………………………………………………… …………………9分
( http: / / www. / )
= ………………………12分
21.解析:(1)由题可得, ,解得,
则,
椭圆的方程为; -----------------2分
(2)∵点是圆上的动点,∴, -----------------3分
设椭圆的左焦点为,依据椭圆的定义知,, ----------------5分
∴,
当点是延长线与椭圆的交点时,取得最大值,
∴的最大值为, -------------------7分
此时直线的方程是,
点的坐标是方程组的解,消去得,, -------------------9分
解得,根据图形可知,, -------------------10分
此时的点坐标为(,). -------------------12分
22. 解:设函数(Ⅰ)当曲线处的切线方程(Ⅱ)求函数的单调区间与极值;(Ⅲ)已知函数有三个互不相同的零点0,,且。若对任意的,恒成立,求m的取值范围。
解析 当所以曲线处的切线斜率为1. 又,所以曲线处的切线方程为. …………………………………………………………………………2分
(2)解析,令,得到
因为 当x变化时,的变化情况如下表:
+ 0 - 0 +
极小值 极大值
………………………………4
在和内减函数,在内增函数。
函数在处取得极大值,且=………………5分
函数在处取得极小值,且
= ……………………………………………………………………6分
(3)解析 由题设,
所以方程=0由两个相异的实根,故,且,解得 ………………………………………………………………………8分
因为
若,而,不合题意……………………9分
若则对任意的有 ………………………………10分
则又,所以函数在的最小值为0,于是对任意的,恒成立的充要条件是,解得
综上,m的取值范围是 ………………………………………………… 12分
2
4
2
2
2
2
正视图
侧视图
俯视图
主视图
1
左视图
2
俯视图
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
2014-2015学年第一学期河北省保定市八校联合体高三期中联考
高三数学(文科)
(满分150分,考试时间:120分钟)
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟,注意事项:
1.第Ⅰ卷的答案填在答题卷方框里,第Ⅱ卷的答案或解答过程写在答题卷指定处,写在试题卷上的无效。
2.答题前,考生务必将自己的“姓名”、“班级”、和“考号”写在答题卷上。
3.考试结束,只交答题卷。
第Ⅰ卷(选择题共60分)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的,把答案填涂在答题卷相应位置上)21世纪教育网版权所有
1.已知,若共线,则实数x=
A. B. C.1 D.2
2.命题:“”的否定为
A. B.
C. D.
3.把函数的图象向左平移个单位长度后,所得到的图象关于y轴对称,则m的最小值是
A. B. C. D.
4数f (x)=+3x的零点个数是
(A) 0 (B) 1 (C) 2 (D) 321教育网
5已知直线l∥平面α,P∈α,那么过点P且平行于直线l的直线
(A) 只有一条,不在平面α内
(B) 有无数条,不一定在平面α内
(C) 只有一条,且在平面α内
(D) 有无数条,一定在平面α内
6 ( http: / / www. / )为非零向量“函数为偶函数”是“ ( http: / / www. / )”的
A.充分不必要条件 ( http: / / www. / ) B. 必要不充分条件
C.充要条件 D. 既不充分又不必要条件
7某几何体的三视图 (单位:cm) 如图所示,则此几何体的体积是
(A) 36 cm3 (B) 48 cm3
(C) 60 cm3 (D) 72 cm3
8函数,则y的取值范围是
A. B. C. D.
9已知 ( http: / / www. / )是内的一点,且 ( http: / / www. / ),则 ( http: / / www. / )、和 ( http: / / www. / )的面积分别为;则 ( http: / / www. / )的最小值为
A.20 B.19 C.16 D.1821cnjy.com
10.列是首项为1,公比为的等比数列,则等于
A.-32 B.32 C.-64 D.64
11.外接圆的圆心为,半径为,且,则向量 在方向上的投影为
A. B. C. D.
12.已知数列满足:,用[x]表示不超过x的最大整数,则
的值等于
A.0 B.1 C.2 D.3
第II卷(非选择题共90分)
二、填空题(本大题共4小题,每小题5分,共20分,把答案填在答题卷相应位置上)
13.=
14已知 ( http: / / www. / )为等差数列,, ( http: / / www. / )为其前n项和,则使达到最大值的n等于__ ( http: / / www. / )_________.
15某圆锥体的底面半径,沿圆锥体的母线把侧面展开后可得到圆心角为的扇形,则该圆锥体的体积是 . www.21-cn-jy.com
16若对任意m∈R,直线x+y+m=0都不是曲线的切线,则实数a的取值范围是____________. 2·1·c·n·j·y
三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)
17(本小题满分12分)
已知函数
①求函数 ( http: / / www. / )的最小正周期;
②在中, ( http: / / www. / )为内角的对边,若 ( http: / / www. / ),求 ( http: / / www. / )的最大面积。
18(本小题满分12分)
一个三棱柱的直观图和三视图如图所示(主视图、俯视图都是矩形,左视图是直角三角形),设为线段上的点.【来源:21·世纪·教育·网】
(1)求几何体的体积;
(2)是否存在点E,使平面平面,若存在,求AE的长.
19(本小题满分12分)
我省城乡居民社会养老保险个人年缴费分1 ( http: / / www.21cnjy.com )00,200,300,400,500,600,700,800,900,1000(单位元)十个档次,某社区随机抽取了50名村民,按缴费在100~500元,600~1000元,以及年龄在20~39岁,40~59岁之间进行了统计,相关数据如下:21·cn·jy·com
( http: / / www.21cnjy.com )
(1)用分层抽样的方法在缴费100~500元之间的村民中随机抽取5人,则年龄在20~39岁之间应抽取几人?21·世纪*教育网
(2)在(1)的条件下抽取的5人中,随机选取2人进行到户走访,求这2人的年龄都在40~59岁之间的概率。www-2-1-cnjy-com
(3)能否有95%的把握认为缴费的档次与年龄有关?
( http: / / www.21cnjy.com )
20.小题满分12分)
等差数列的前n项的和为 ( http: / / www. / ),且
(1)求 ( http: / / www. / )的通项公式;
(2)若数列满足 ( http: / / www. / ),且设数列 ( http: / / www. / )的前n项和为.
求证: ( http: / / www. / ).
21(本题满分12分)
椭圆:的右焦点,离心率为,已知点坐标是,点是椭圆上的动点.
(1)求椭圆的方程;
(2)求的最大值及此时的点坐标.
22. (本小题满分12分)设函数
(1)当曲线处的切线方程
(2)求函数的单调区间与极值;
(3)已知函数有三个互不相同的零点0,,且。若对任意的,恒成立,求m的取值范围。
文科数学参考答案
一、选择题 BBCBC DCBCB CB
二、填空题
13.;14.5;15.;16.;
三 ( http: / / www. / )、解答题
17.解:①由已知
( http: / / www. / ) ……………………………… 6分
②由①知,即 ( http: / / www. / )
又∴ ( http: / / www. / )
当且仅当 ( http: / / www. / )时, …………………………………………12分
18.解:(Ⅰ)由题可知,三棱柱为直三棱柱,底面,
且底面是直角三角形, ,,…………2分
三棱柱的体积…………4分
(Ⅱ)三棱柱为直三棱柱,底面,
,,又,
, ………………6分
又平面, …………………9分
由,,,得平面,
又平面,平面平面. ……………12分
19(Ⅰ)设抽取人,则,,所以在20~39岁之间应抽取2人.
…………………3分
(Ⅱ)记在缴费100~500元之间抽取的5人中,年龄20~39的两人为,
年龄40~59 岁的三人为, 所以随机抽取2人的所有情况有:
10种,其中年龄都在40~59岁之间有3种,故……………………8分
(III),因为,所以没有的把握认为缴费档次和年龄有关. ………………………………………………12分
20. 解:1) ( http: / / www. / ), 由
解得 ( http: / / www. / ) 又
所以 ( http: / / www. / ) ……………………………………………………… …………………4
2)
( http: / / www. / )
。。。。。。
( http: / / www. / )
叠加得
所以 ( http: / / www. / )………………………………………………………………… …………………9分
( http: / / www. / )
= ………………………12分
21.解析:(1)由题可得, ,解得,
则,
椭圆的方程为; -----------------2分
(2)∵点是圆上的动点,∴, -----------------3分
设椭圆的左焦点为,依据椭圆的定义知,, ----------------5分
∴,
当点是延长线与椭圆的交点时,取得最大值,
∴的最大值为, -------------------7分
此时直线的方程是,
点的坐标是方程组的解,消去得,, -------------------9分
解得,根据图形可知,, -------------------10分
此时的点坐标为(,). -------------------12分
22. 解:设函数(Ⅰ)当曲线处的切线方程(Ⅱ)求函数的单调区间与极值;(Ⅲ)已知函数有三个互不相同的零点0,,且。若对任意的,恒成立,求m的取值范围。
解析 当所以曲线处的切线斜率为1. 又,所以曲线处的切线方程为. …………………………………………………………………………2分
(2)解析,令,得到
因为 当x变化时,的变化情况如下表:
+ 0 - 0 +
极小值 极大值
………………………………4
在和内减函数,在内增函数。
函数在处取得极大值,且=………………5分
函数在处取得极小值,且
= ……………………………………………………………………6分
(3)解析 由题设,
所以方程=0由两个相异的实根,故,且,解得 ………………………………………………………………………8分
因为
若,而,不合题意……………………9分
若则对任意的有 ………………………………10分
则又,所以函数在的最小值为0,于是对任意的,恒成立的充要条件是,解得
综上,m的取值范围是 ………………………………………………… 12分
2
4
2
2
2
2
正视图
侧视图
俯视图
主视图
1
左视图
2
俯视图
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
