24.1.3

课件49张PPT。24.1.3 弧、弦、圆心角茶杯的盖子做成圆
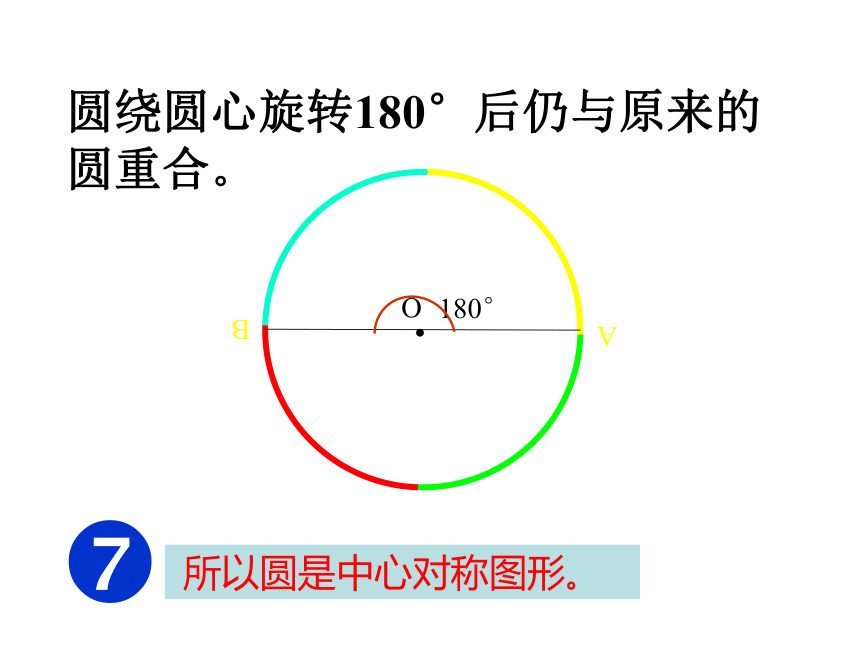
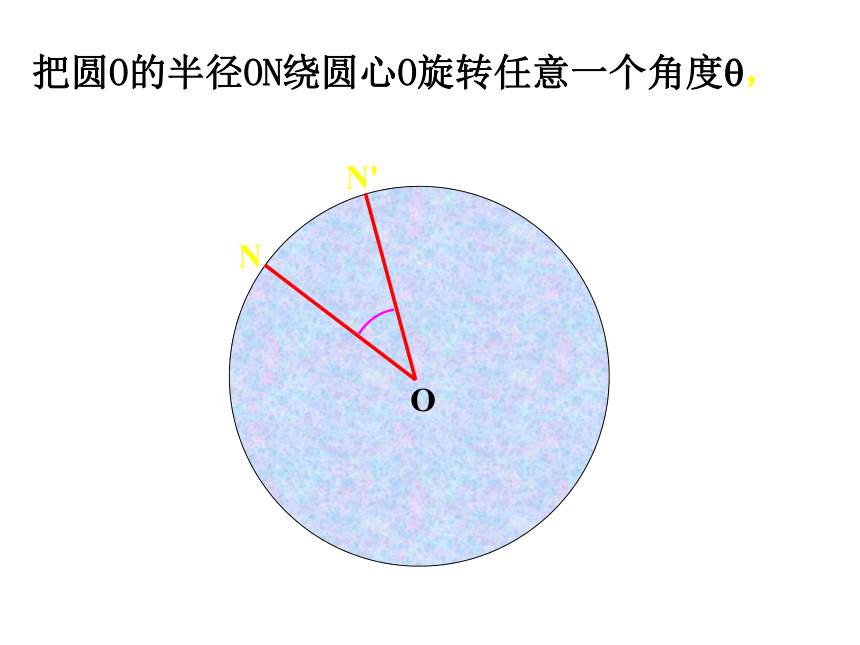
形有什么好处呢？AB圆绕圆心旋转?圆绕圆心旋转?圆绕圆心旋转?圆绕圆心旋转?BA圆绕圆心旋转?圆绕圆心旋转?圆绕圆心旋转?NO把圆O的半径ON绕圆心O旋转任意一个角度?，1、判别下列各图中的角是不是圆心角，
并说明理由。①②③④ABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系？ABCDoABCDoABCDoABCDoABCDoABCDoABCDoABCDoABCDoABCDoABCDoABCDoABCDoABCDoABCDoABCDoABCDoABCDoABCDoABCDo①∠AOB= ∠COD猜想②AB=CDAB=CD
证明:∵OA=OC ，OB=OD，
∠AOB=∠COD,
∴ 当点A与点C重合时，
点B与点D也重合。
∴　AB=CD，
已知:如图∠AOB=∠ COD,
求证: AB=CD，AB = CD。⌒⌒圆心角定理：相等的圆心角所对的弧相等，
所对的弦也相等。在同圆或等圆中，若：①∠AOB= ∠COD②AB=CD则： 如果交换题设和结论，会有一些什么样的结论呢？AB=CD归纳：在同圆或等圆中，两个圆心角、两条弧、两条弦中有一组量相等，它们所对应的其余各组量也相等。①∠AOB= ∠COD②AB=CD只要满足其中一个条件，
另外两个条件必成立。AB=CD练一练：1、如果，AB、CF是⊙O的两条弦：
（1）如果AB=CD，那么 ， 。
（2）如果AB=CD，那么 ， 。
（3）如果∠AOB= ∠COD，那么 ， 。
（4）如果OE⊥AB，OF⊥CD且OE=OF，
那么有何相等关系？ABDCEFO⌒⌒想一想：弦心距相等，则所对应的弧、弦、圆心角有何关系？3、一条弦把圆分成1：3两部分，则弦所对的圆心角为________． 2．下列命题①圆心角是顶点在圆心的角 ②两个圆心角相等，它们所对的弦也相等；③两条弦相等，圆心到这两弦的距离也相等；④在等圆中，圆心角不等，所对的弦也不等，其中正确的命题是 。⌒⌒例：如图,在⊙O中, , ∠ACB= 60°,
求证: ∠AOB=∠BOC=∠AOC
AOCBAB=AC⌒⌒（2）如图，在⊙O中，AC=BD，∠COD=400，
求∠AOB的度数。⌒例.如图，CD是⊙O的弦 ,AC=BD ,OA、
OB分别交CD于E、F. 求证：△OEF是等腰三角形. OACDEFB⌒⌒例．如图所示，已知AB是⊙O的直径，M、N分别是AO、BO的中点，CM⊥AB，DN⊥AB，求证: AC=BDDCABNMO⌒⌒小结----自我挑战本节课我们认识了什么？理解了什么？又学会了什么数学方法呢？