函数的单调性

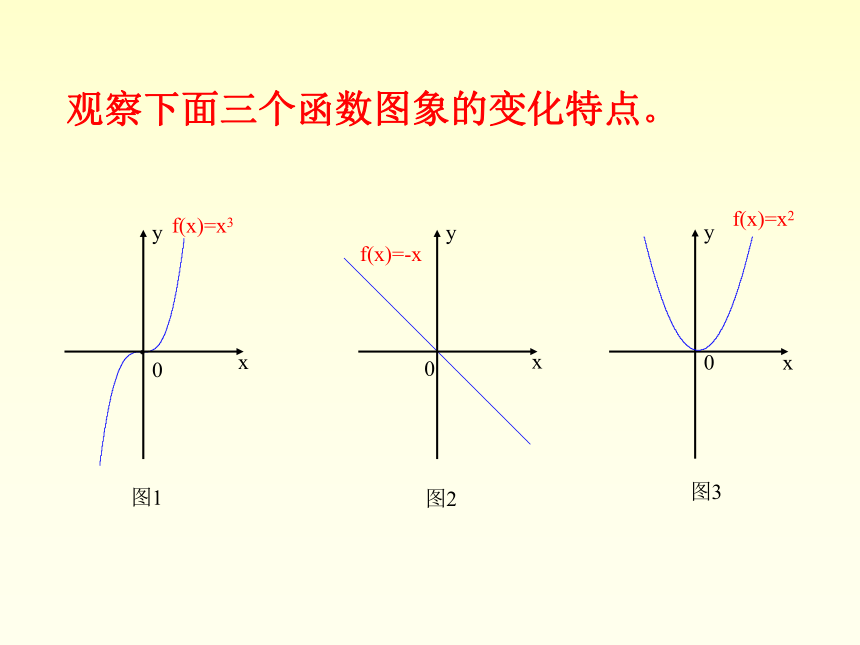
课件14张PPT。函数的单调性（一） f(x)=x3xy0f(x)=-xxy0xy0f(x)=x2图1图2图3观察下面三个函数图象的变化特点。在R上任意取两个值x1、x2
当x1< x2时，都有f(x1) < f(x2) ， f(x)=-x即在R上任意取两个值x1、x2
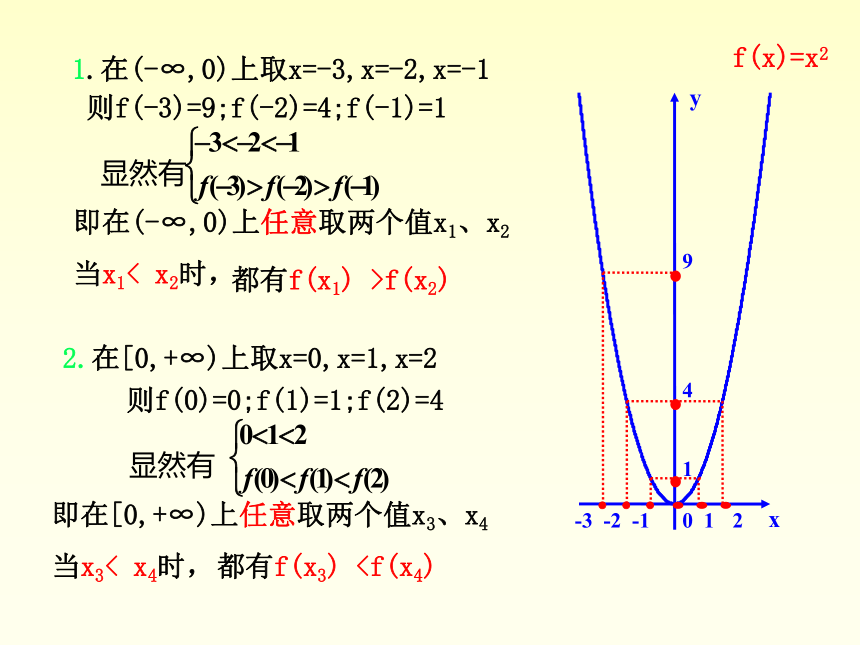
当x1< x2时，都有f(x1) >f(x2) ，1.在(-∞,0)上取x=-3,x=-2,x=-1则f(-3)=9;f(-2)=4;f(-1)=12.在[0,+∞)上取x=0,x=1,x=2则f(0)=0;f(1)=1;f(2)=4即在[0,+∞)上任意取两个值x3、x4
当x3< x4时，即在(-∞,0)上任意取两个值x1、x2
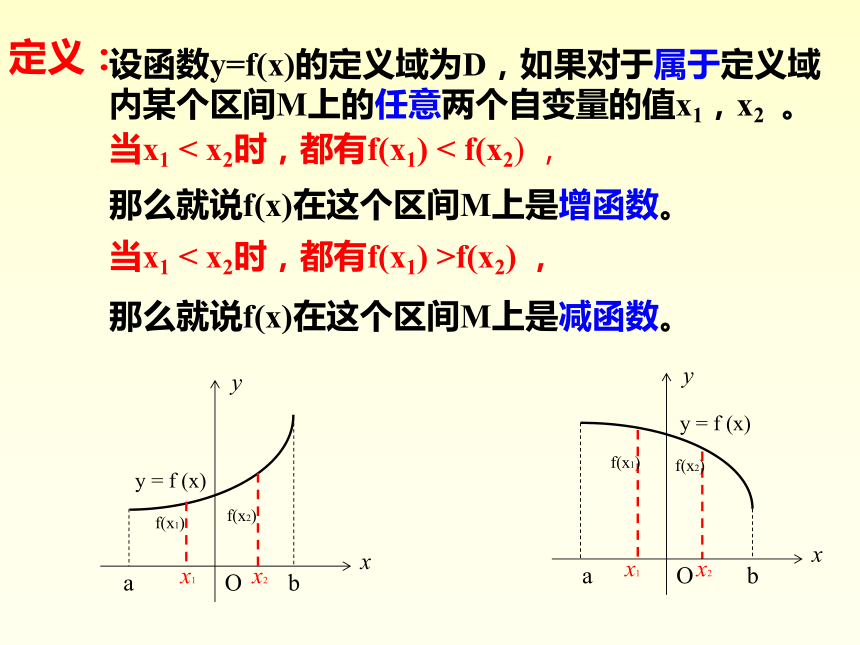
当x1< x2时，f(x)=x2都有f(x1) >f(x2)都有f(x3) f(x2) ，
那么就说f(x)在这个区间M上是减函数。
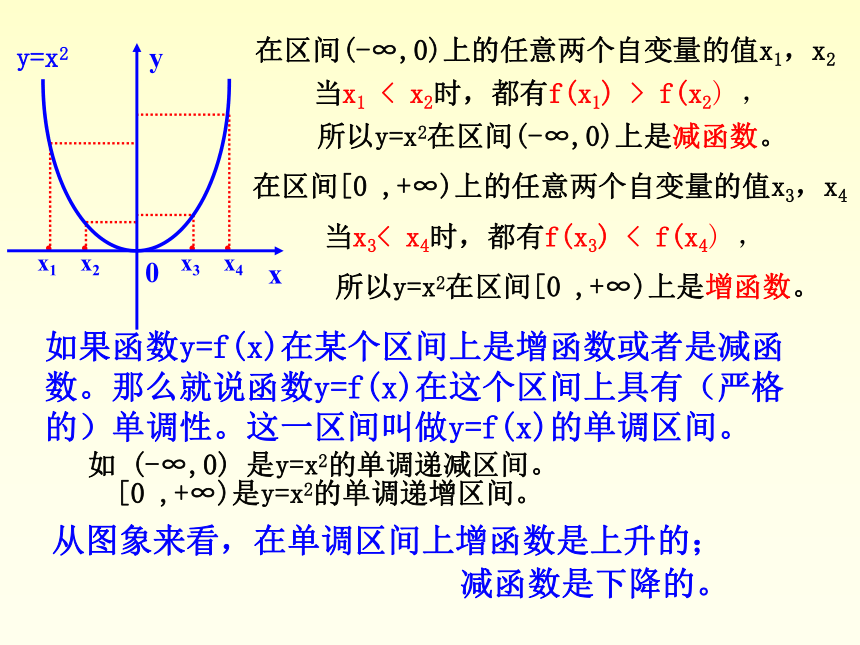
当x1 < x2时，都有f(x1) < f(x2) ， 那么就说f(x)在这个区间M上是增函数。在区间(-∞,0)上的任意两个自变量的值x1，x2 当x1 < x2时，都有f(x1) > f(x2) ，所以y=x2在区间(-∞,0)上是减函数。在区间[0 ,+∞)上的任意两个自变量的值x3，x4 当x3< x4时，都有f(x3) < f(x4) ，所以y=x2在区间[0 ,+∞)上是增函数。如果函数y=f(x)在某个区间上是增函数或者是减函数。那么就说函数y=f(x)在这个区间上具有（严格的）单调性。这一区间叫做y=f(x)的单调区间。（函数在一个点上没有单调性）解：单调递减单调递减反例：取x1= - 1 , x2=1，则f(-1)=-1,f(1)=1
可见 x1 < x2 时; f(x1) > f(x2)不一定成立。例1：如图是定义在闭区间[-5,5]上的函数y=f(x)的图象，根据图象说出y=f(x)的单调区间，以及在每一个单调区间上，y=f(x)是增函数还是减函数。答：函数y=f(x)的单调区间有
[-5,-2),[-2,1), [1,3), [3,5];其中 单调减区间是 [-5,-2), [1,3) ，单调增区间是 [-2,1), [3,5] 。例2 （1）证明函数f(x)=-3x+2在R上是减函数。证明：设x1,x2是R上的任意两个实数，且 x1 且0≤ x1 < x2 ,则于是 f(x1)-f(x2)＜0。即 f(x1)＜f(x2)取值作差变形定号判断证明:例3：写出f(x)=x2－4x+5的单调递增区间，并证明。所以f(x)=x2－4x+5的单调递增区间为[2, +∞）2通过观察函数图象，对函数是否具有某种性质作出一种猜想，然后通过推理的方法，证明这种猜想的正确性。这是发现问题和解决问题的一种常用数学方法。即先猜后证。15 1:求证函数 y=x3在R上是增函数.练习:课堂小结1. 函数单调性定义。2. 单调性的证明步骤。取值定号变形作差判断