椭圆及其标准方程 第二课时 校公开课(江苏省南京市)
文档属性
| 名称 | 椭圆及其标准方程 第二课时 校公开课(江苏省南京市) |

|
|
| 格式 | rar | ||
| 文件大小 | 63.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-17 00:00:00 | ||
图片预览




文档简介
课件12张PPT。椭圆及其标准方程(2)温故知新求动点的轨迹常采用的方法有:1、直接法:(转移、代入法)建系设点列式化简2、相关点法:3、参数法:其特点是:动点M(x,y)的坐标取决于已知曲线C上的
点P(x′,y ′)的坐标,可先用x,y来
表示x′,y ′ ,再代入曲线C的方程,
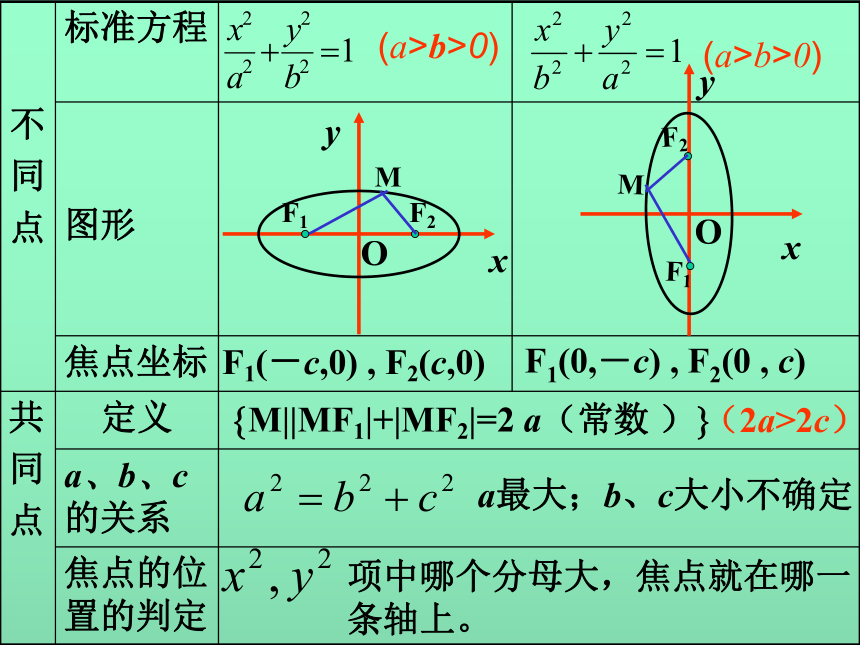
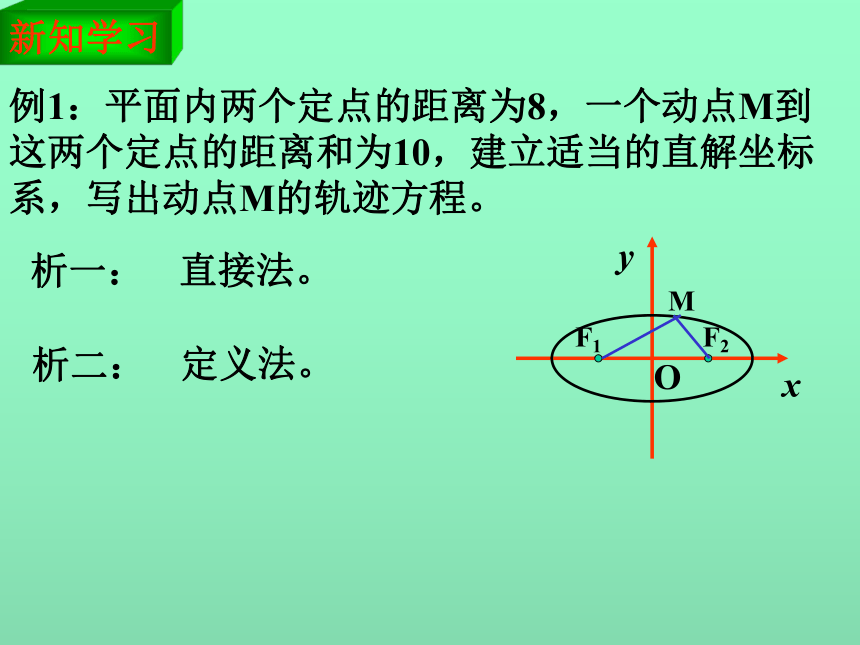
即得点M的轨迹方程4、定义法:特点:已知曲线类型,求曲线方程。(a>b>0)(a>b>0)项中哪个分母大,焦点就在哪一条轴上。F1(-c,0) , F2(c,0)F1(0,-c) , F2(0 , c)a最大;b、c大小不确定?M||MF1|+|MF2|=2 a(常数 )?(2a>2c)新知学习例1:平面内两个定点的距离为8,一个动点M到
这两个定点的距离和为10,建立适当的直解坐标
系,写出动点M的轨迹方程。xOyF1F2析一:直接法。析二:定义法。新知学习例1:平面内两个定点的距离为8,一个动点M到这两个定点的距离和为10,建立适当的直解坐标系,写出动点M的轨迹方程。xOyF1F2解:(直接法)设两定点分别为F1, F2 , 以F1, F2 所在直线为x轴, F1 F2
的中垂线为y轴,建立坐标系如图。 则F1(-4,0), F2(4,0), 设M (x, y), 由|MF1|+|MF2|=10得:化简得:∴动点M的轨迹方程为:新知学习例1:平面内两个定点的距离为8,一个动点M到这两个定点的距离和为10,建立适当的直解坐标系,写出动点M的轨迹方程。解:(定义法)设两定点分别为F1, F2 , 以F1, F2 所在直线为x轴, F1 F2
的中垂线为y轴,建立坐标系如图。 ∴动点M的轨迹方程为:由题意知:点M的轨迹是以两定点为焦点的椭圆。∵ 2 a=10, 2c=8∴ a=5, c=4∴ b2= a2-c2=25-16=9新知学习xOy例2:已知B、C是两个定点,|BC|=6,且△ABC的周长等于16,求顶点A的轨迹方程。析一:直接法析二:定义法以B、C 所在直线为x轴, BC的中垂线为y轴,建立坐标系如图。 ∴动点A的轨迹方程为:∴点A的轨迹是以两定点B、C为焦点的椭圆。∵ 2 a=10, 2c=6∴ a=5, c=3∴ b2= 25-9=16解:∵|AB|+|BC|+|AC|=16, |BC|=6∴|AB|+|AC|=10当点A在直线BC上时,A、B、C不能构成三角形。(y≠0)新知学习例3:已知一个圆的圆心为坐标原点,半径为2,从这个圆上任一点P向轴作垂线段PP′,求线段PP′中点M的轨迹。析一:题中有两个动点P、M点M随点P动而动P点主动点M点被动点(相关点法)新知学习例3:已知一个圆的圆心为坐标原点,半径为2,从这个圆上任一点P向轴作垂线段PP′,求线段PP′中点M的轨迹。解:设点M (x, y),点P (x′, y′) 则x′= x, y′=2y∴P(x,2y)∵点P在圆x2 + y2=4上∴ x2 + (2y)2=4即:∴ 点M轨迹方程为:故点M的轨迹是一个椭圆。新知学习例3:已知一个圆的圆心为坐标原点,半径为2,从这个圆上任一点P向轴作垂线段PP′,求线段PP′中点M的轨迹。析二:参数法。(参见教材P80例6,P81练习3)由此知:将圆按照某一个方向均匀地
压缩或拉长,可以得到椭圆。知识小结:求轨迹(曲线)方程常用方法:1、直接法2、相关点法3、参数法4、定义法作业:1、认真体会求轨迹(曲线)方程常用方法,
并找相关题进行练习,以便熟练掌握。2、教材P96练习4、习题2、5、6、73、预习8.2椭圆的简单几何性质。
点P(x′,y ′)的坐标,可先用x,y来
表示x′,y ′ ,再代入曲线C的方程,
即得点M的轨迹方程4、定义法:特点:已知曲线类型,求曲线方程。(a>b>0)(a>b>0)项中哪个分母大,焦点就在哪一条轴上。F1(-c,0) , F2(c,0)F1(0,-c) , F2(0 , c)a最大;b、c大小不确定?M||MF1|+|MF2|=2 a(常数 )?(2a>2c)新知学习例1:平面内两个定点的距离为8,一个动点M到
这两个定点的距离和为10,建立适当的直解坐标
系,写出动点M的轨迹方程。xOyF1F2析一:直接法。析二:定义法。新知学习例1:平面内两个定点的距离为8,一个动点M到这两个定点的距离和为10,建立适当的直解坐标系,写出动点M的轨迹方程。xOyF1F2解:(直接法)设两定点分别为F1, F2 , 以F1, F2 所在直线为x轴, F1 F2
的中垂线为y轴,建立坐标系如图。 则F1(-4,0), F2(4,0), 设M (x, y), 由|MF1|+|MF2|=10得:化简得:∴动点M的轨迹方程为:新知学习例1:平面内两个定点的距离为8,一个动点M到这两个定点的距离和为10,建立适当的直解坐标系,写出动点M的轨迹方程。解:(定义法)设两定点分别为F1, F2 , 以F1, F2 所在直线为x轴, F1 F2
的中垂线为y轴,建立坐标系如图。 ∴动点M的轨迹方程为:由题意知:点M的轨迹是以两定点为焦点的椭圆。∵ 2 a=10, 2c=8∴ a=5, c=4∴ b2= a2-c2=25-16=9新知学习xOy例2:已知B、C是两个定点,|BC|=6,且△ABC的周长等于16,求顶点A的轨迹方程。析一:直接法析二:定义法以B、C 所在直线为x轴, BC的中垂线为y轴,建立坐标系如图。 ∴动点A的轨迹方程为:∴点A的轨迹是以两定点B、C为焦点的椭圆。∵ 2 a=10, 2c=6∴ a=5, c=3∴ b2= 25-9=16解:∵|AB|+|BC|+|AC|=16, |BC|=6∴|AB|+|AC|=10当点A在直线BC上时,A、B、C不能构成三角形。(y≠0)新知学习例3:已知一个圆的圆心为坐标原点,半径为2,从这个圆上任一点P向轴作垂线段PP′,求线段PP′中点M的轨迹。析一:题中有两个动点P、M点M随点P动而动P点主动点M点被动点(相关点法)新知学习例3:已知一个圆的圆心为坐标原点,半径为2,从这个圆上任一点P向轴作垂线段PP′,求线段PP′中点M的轨迹。解:设点M (x, y),点P (x′, y′) 则x′= x, y′=2y∴P(x,2y)∵点P在圆x2 + y2=4上∴ x2 + (2y)2=4即:∴ 点M轨迹方程为:故点M的轨迹是一个椭圆。新知学习例3:已知一个圆的圆心为坐标原点,半径为2,从这个圆上任一点P向轴作垂线段PP′,求线段PP′中点M的轨迹。析二:参数法。(参见教材P80例6,P81练习3)由此知:将圆按照某一个方向均匀地
压缩或拉长,可以得到椭圆。知识小结:求轨迹(曲线)方程常用方法:1、直接法2、相关点法3、参数法4、定义法作业:1、认真体会求轨迹(曲线)方程常用方法,
并找相关题进行练习,以便熟练掌握。2、教材P96练习4、习题2、5、6、73、预习8.2椭圆的简单几何性质。
