双曲线的几何性质 第一课时(江苏省南京市)
文档属性
| 名称 | 双曲线的几何性质 第一课时(江苏省南京市) |

|
|
| 格式 | rar | ||
| 文件大小 | 108.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-17 00:00:00 | ||
图片预览






文档简介
课件18张PPT。双曲线的几何性质第 一 课 时目标1.能运用类比的学习方法,掌握双曲线的几何性质(范围、对称性、项点、渐近线、离心率);
2.理解渐近线的概念,离心率的大小对双曲线的影响,明确各量的几何意义;
3.了解等轴双曲线的概念的特征;
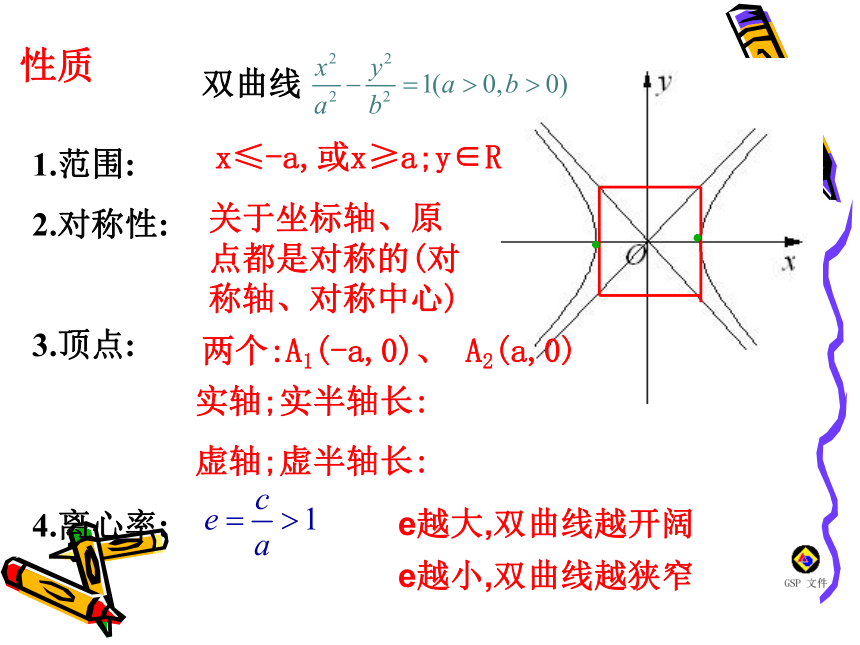
4.能运用双曲线的几何性质或图形特征,确定焦点位置,求双曲线的标准方程.回顾椭圆的几何性质及研究方法见图表双曲线的几何性质类比椭圆,探讨双曲线 的几何性质:范围、对称性、顶点、离心率.双曲线1.范围:
2.对称性:
3.顶点:
4.离心率:x≤-a,或x≥a;y∈R关于坐标轴、原点都是对称的(对称轴、对称中心)两个:A1(-a,0)、 A2(a,0)实轴;实半轴长:
虚轴;虚半轴长:e越大,双曲线越开阔
e越小,双曲线越狭窄性质5.渐近线(1)渐近线方程:(2)渐近线的证明:令 中的1为0,再化简所得的直线方程.(3)渐近线的应用:较准确地画出双曲线的草图.你能说出学过的其它曲线的渐近线吗?(4)等轴双曲线:实轴和虚轴等长的双曲线——等轴双曲线.等轴双曲线的离心率为——等轴双曲线的两渐近线为y=±x,互相垂直(所在角为90°).(2000高考)双曲线 的两条渐近线互相垂直,那么该双曲线的离心率是
A.2 B. C. D.双曲线见图表P113 练习5:当渐近线方程为 时,双曲线的标准方程一定是 吗?如果不一定,举一反例.特征三角形的说明.(2)、求焦点在Y轴上,焦距是16,e= 的双曲线方程?课堂练习:1.求下列双曲线的实轴与虚轴长,顶点,焦点坐标, 及渐近线方程.
2、求与椭圆 有公共焦点且离心率
e= 的双曲线方程3、求经过点A(3,-1)并且对称轴都在坐标轴上的等轴双曲线。将点A(3,-1)代入有9-1=k,k=8,
故方程解 因为是等轴双曲线,所以设双曲线方程为例题1.求双曲线9x2-16y2=144的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程。2.求满足下列条件的双曲线的标准方程:
(1)以2x±3y=0为渐近线,且过点(1,2); (2)与椭圆x2+5y2=5共焦点且一条渐近线方程为
(3)离心率为5/4,虚半轴长为2.共渐近线双曲线的方程的设法:
以bx±ay=0为渐近线的双曲线可设为b2x2-a2y2=λ(λ≠0)3. 双曲线型自然通风塔的外形是双曲线的一部分绕其虚轴旋转所成的曲面。它的最小半径为12米,上口半径为13米,下口半径为25米,高55米,选择适当的坐标系,求出此双曲线方程(精确到1米)。分析(1)此题是一个应用问题,没
有坐标系.你准备如何选择坐标系?(2).最小半径为12米意味着什么?(3)上口端点C的坐标(13,y)
那么下口端点B的坐标是(_?,_?_)故用待定系数法.解 取最小圆直径AA1所在直线为x轴,其圆心为坐标原点建系. 则 上,下口直径CC1,BB1平行于x轴,且|CO1|=13,|BO2|=25,|O1O2|=55设 双曲线方程为
令C(13,y),则B(25,y-55),又B,C在双曲线上,
所以
∴b≈25故所求双曲线方程为CBAA1C1O1O20yxB1实际应用问题要注意
(1)选择适当的数学模式(本题为双曲线
的第一类型标准方程;
(2)选择适当的坐标系
(3)正确列式并求解;
(4)作答(回到实际问题中去)1.两种标准方程的双曲线的几何性质及比较
2.等轴双曲线及其性质
3.共渐近线双曲线方程的设法小结作业1.P114习题6(作为结论记住)
2.过双曲线的一个焦点F2作实轴的垂线交双曲线于P,Q两点,F1是双曲线的另一个焦点,且∠PF1Q=60°,求双曲线的离心率.
3.已知双曲线 的两条渐近线的夹角为2θ,离心率为e,求证:思考:若b>a>0呢?
2.理解渐近线的概念,离心率的大小对双曲线的影响,明确各量的几何意义;
3.了解等轴双曲线的概念的特征;
4.能运用双曲线的几何性质或图形特征,确定焦点位置,求双曲线的标准方程.回顾椭圆的几何性质及研究方法见图表双曲线的几何性质类比椭圆,探讨双曲线 的几何性质:范围、对称性、顶点、离心率.双曲线1.范围:
2.对称性:
3.顶点:
4.离心率:x≤-a,或x≥a;y∈R关于坐标轴、原点都是对称的(对称轴、对称中心)两个:A1(-a,0)、 A2(a,0)实轴;实半轴长:
虚轴;虚半轴长:e越大,双曲线越开阔
e越小,双曲线越狭窄性质5.渐近线(1)渐近线方程:(2)渐近线的证明:令 中的1为0,再化简所得的直线方程.(3)渐近线的应用:较准确地画出双曲线的草图.你能说出学过的其它曲线的渐近线吗?(4)等轴双曲线:实轴和虚轴等长的双曲线——等轴双曲线.等轴双曲线的离心率为——等轴双曲线的两渐近线为y=±x,互相垂直(所在角为90°).(2000高考)双曲线 的两条渐近线互相垂直,那么该双曲线的离心率是
A.2 B. C. D.双曲线见图表P113 练习5:当渐近线方程为 时,双曲线的标准方程一定是 吗?如果不一定,举一反例.特征三角形的说明.(2)、求焦点在Y轴上,焦距是16,e= 的双曲线方程?课堂练习:1.求下列双曲线的实轴与虚轴长,顶点,焦点坐标, 及渐近线方程.
2、求与椭圆 有公共焦点且离心率
e= 的双曲线方程3、求经过点A(3,-1)并且对称轴都在坐标轴上的等轴双曲线。将点A(3,-1)代入有9-1=k,k=8,
故方程解 因为是等轴双曲线,所以设双曲线方程为例题1.求双曲线9x2-16y2=144的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程。2.求满足下列条件的双曲线的标准方程:
(1)以2x±3y=0为渐近线,且过点(1,2); (2)与椭圆x2+5y2=5共焦点且一条渐近线方程为
(3)离心率为5/4,虚半轴长为2.共渐近线双曲线的方程的设法:
以bx±ay=0为渐近线的双曲线可设为b2x2-a2y2=λ(λ≠0)3. 双曲线型自然通风塔的外形是双曲线的一部分绕其虚轴旋转所成的曲面。它的最小半径为12米,上口半径为13米,下口半径为25米,高55米,选择适当的坐标系,求出此双曲线方程(精确到1米)。分析(1)此题是一个应用问题,没
有坐标系.你准备如何选择坐标系?(2).最小半径为12米意味着什么?(3)上口端点C的坐标(13,y)
那么下口端点B的坐标是(_?,_?_)故用待定系数法.解 取最小圆直径AA1所在直线为x轴,其圆心为坐标原点建系. 则 上,下口直径CC1,BB1平行于x轴,且|CO1|=13,|BO2|=25,|O1O2|=55设 双曲线方程为
令C(13,y),则B(25,y-55),又B,C在双曲线上,
所以
∴b≈25故所求双曲线方程为CBAA1C1O1O20yxB1实际应用问题要注意
(1)选择适当的数学模式(本题为双曲线
的第一类型标准方程;
(2)选择适当的坐标系
(3)正确列式并求解;
(4)作答(回到实际问题中去)1.两种标准方程的双曲线的几何性质及比较
2.等轴双曲线及其性质
3.共渐近线双曲线方程的设法小结作业1.P114习题6(作为结论记住)
2.过双曲线的一个焦点F2作实轴的垂线交双曲线于P,Q两点,F1是双曲线的另一个焦点,且∠PF1Q=60°,求双曲线的离心率.
3.已知双曲线 的两条渐近线的夹角为2θ,离心率为e,求证:思考:若b>a>0呢?
