人教A版必修二 第十章概率复习课(1) 课件(共22张PPT)
文档属性
| 名称 | 人教A版必修二 第十章概率复习课(1) 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 561.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-20 10:38:29 | ||
图片预览








文档简介
(共22张PPT)
概率 复习课
高中数学 一年级
解析:试验的全部样本点为
(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6),
共36个.
D
例1:“连续抛掷两枚质地均匀的骰子,记录朝上的点数”,该试验的样本点共有( )
A.6个 B.12个
C.24个 D.36个
练习1:现在甲、乙、丙三人玩剪刀、石头、布的出拳游戏,观察其出拳情况.
(1)写出该试验的样本空间;
(2)“三人出拳相同”包含的样本点有哪些?
解析:以(J,S,B)表示三人中甲出剪刀、乙出石头、丙出布.
(1)Ω={(J,J,J),(J,J,S),(J,S,J),(S,J,J),(J,J,B),(J,B,J),(B,J,J),(J,S,S),(S,J,S),(S,S,J),(J,B,B),(B,J,B),(B,B,J),(S,S,S),(S,S,B),(S,B,S),(B,S,S),(B,B,S),(B,S,B),(S,B,B),(B,B,B),(J,S,B),(J,B,S),(S,J,B),(S,B,J),(B,J,S),(B,S,J)}.
(2)“三人出拳相同”包含下列三个基本事件:
(J,J,J),(S,S,S),(B,B,B).
确定试验的样本空间的注意点
(1)写试验的样本点时,要按照一定的顺序,避免重复和遗漏,常用的方法有列举法,列表法和树状图法等.
(2)写试验的样本空间最终要写成集合的形式.
例2:从装有两个红球和两个黑球的口袋内任取两个球,那么互斥而不对立的两个事件是( )
A.“至少有一个黑球”与“都是黑球”
B.“至少有一个黑球”与“至少有一个红球”
C.“恰有一个黑球”与“恰有两个黑球”
D.“至少有一个黑球”与“都是红球”
解析:A中的两个事件能同时发生,故不互斥;同样,B中两个事件也可同时发生,故不互斥;D中两个事件是对立的,故选C.
C
练习2:从装有3个红球和4个白球的口袋中任取3个小球,事件“两个红球,一个白球”的互斥事件可以是_________________________________.
(答案不唯一,写出一个即可)
解析:事件“两个红球,一个白球”与事件“两个白球, 一个红球”不可能同时发生,是互斥事件.
例3:从甲、乙、丙、丁、戊五个人中选取三人参加演讲比赛,则甲、乙都当选的概率为( )
A. B.
C. D.
解析:设从五个人中选取三人中有甲乙为事件A,则试验包含10个等可能的样本点甲乙丙,甲乙丁,甲乙戊,甲丙丁,甲丙戊,甲丁戊,乙丙丁,乙丙戊,乙丁戊,丙丁戊,而甲、乙都当选的包含3个样本点,故所求的概率为 P(A)= .
C
练习3:有五根细木棒,长度分别为1,3,5,7,9(cm),从中任取三根,能搭成三角形的概率是( )
A. B. C. D.
解析:设取出的三根木棒能搭成三角形为事件A,试验的样本空间Ω={(1,3,5), (1,3,7),(1,3,9),(1,5,7), (1,5,9), (1,7,9), (3,5,7),(3,5,9),(3,7,9),(5,7,9)},样本点的总数为10,由于三角形两边之和大于第三边,构成三角形的样本点只有(3,5,7), (3,7,9),(5,7,9)三种情况,故所求概率
为P(A)=
D
例四:如图所示,靶子由一个中心圆面Ⅰ和两个同心圆环Ⅱ、Ⅲ构成,射手命中Ⅰ、Ⅱ、Ⅲ的概率分别为0.35,0.30,0.25,则命不中靶的概率是______.
解析:“射手命中圆面Ⅰ”为事件A,“命中圆环Ⅱ”为事件B,“命中圆环Ⅲ”为事件C,“命不中靶”为事件D,则A,B,C彼此互斥,故射手中靶的概率为P(A∪B∪C)=P(A)+P(B)+P(C)=0.35+0.30+0.25=0.90.因为中靶和不中靶是对立事件,故命不中靶的概率为P(D)=1-P(A∪B∪C)=1-0.90=0.10.
0.1
例五:如图所示,A,B,C表示3个开关,若在某段时间内,它们正常工作的概率分别为0.9,0.8,0.7,则该系统的可靠性(3个开关只要一个开关正常工作即可靠)为( )
A.0.504 B.0.994
C.0.496 D.0.064
解析:记A,B,C正常工作为别为P(A),P(B),P(C),则P(A)=0.9, P(B)=0.8, P(C)=0.7由题意可知,三个开关工作与否相互独立,系统不可靠即为3个开关都不工作,
所以考虑对立事件,系统可靠性
1-(1-0.9)×(1-0.8)×(1-0.7)=1-0.006=0.994.
B
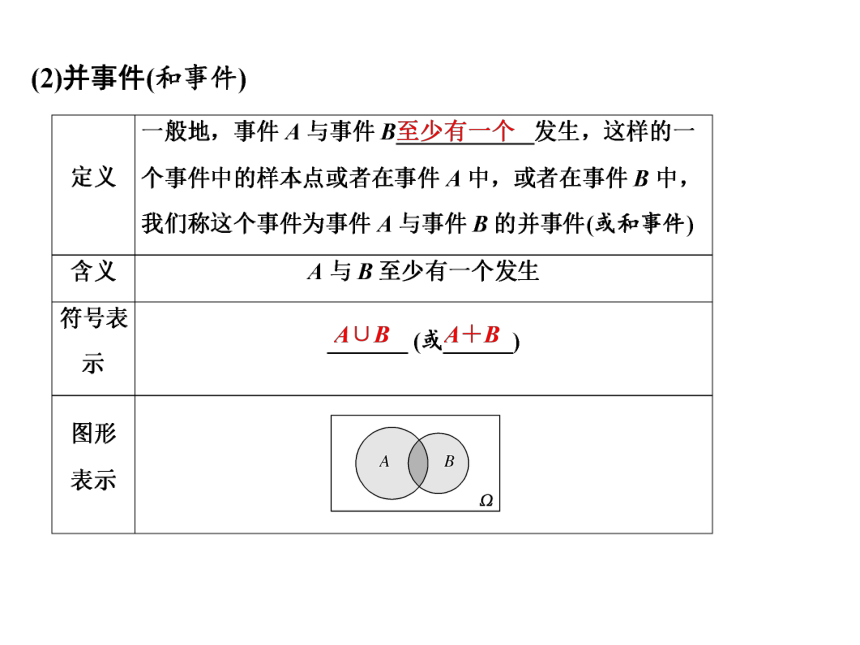
三、课堂小结
1、概率的基本性质
2、事件间的关系和运算
3、古典概型概率问题的求解
4、相互独立事件同时发生概率问题的求解
概率 复习课
高中数学 一年级
解析:试验的全部样本点为
(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6),
共36个.
D
例1:“连续抛掷两枚质地均匀的骰子,记录朝上的点数”,该试验的样本点共有( )
A.6个 B.12个
C.24个 D.36个
练习1:现在甲、乙、丙三人玩剪刀、石头、布的出拳游戏,观察其出拳情况.
(1)写出该试验的样本空间;
(2)“三人出拳相同”包含的样本点有哪些?
解析:以(J,S,B)表示三人中甲出剪刀、乙出石头、丙出布.
(1)Ω={(J,J,J),(J,J,S),(J,S,J),(S,J,J),(J,J,B),(J,B,J),(B,J,J),(J,S,S),(S,J,S),(S,S,J),(J,B,B),(B,J,B),(B,B,J),(S,S,S),(S,S,B),(S,B,S),(B,S,S),(B,B,S),(B,S,B),(S,B,B),(B,B,B),(J,S,B),(J,B,S),(S,J,B),(S,B,J),(B,J,S),(B,S,J)}.
(2)“三人出拳相同”包含下列三个基本事件:
(J,J,J),(S,S,S),(B,B,B).
确定试验的样本空间的注意点
(1)写试验的样本点时,要按照一定的顺序,避免重复和遗漏,常用的方法有列举法,列表法和树状图法等.
(2)写试验的样本空间最终要写成集合的形式.
例2:从装有两个红球和两个黑球的口袋内任取两个球,那么互斥而不对立的两个事件是( )
A.“至少有一个黑球”与“都是黑球”
B.“至少有一个黑球”与“至少有一个红球”
C.“恰有一个黑球”与“恰有两个黑球”
D.“至少有一个黑球”与“都是红球”
解析:A中的两个事件能同时发生,故不互斥;同样,B中两个事件也可同时发生,故不互斥;D中两个事件是对立的,故选C.
C
练习2:从装有3个红球和4个白球的口袋中任取3个小球,事件“两个红球,一个白球”的互斥事件可以是_________________________________.
(答案不唯一,写出一个即可)
解析:事件“两个红球,一个白球”与事件“两个白球, 一个红球”不可能同时发生,是互斥事件.
例3:从甲、乙、丙、丁、戊五个人中选取三人参加演讲比赛,则甲、乙都当选的概率为( )
A. B.
C. D.
解析:设从五个人中选取三人中有甲乙为事件A,则试验包含10个等可能的样本点甲乙丙,甲乙丁,甲乙戊,甲丙丁,甲丙戊,甲丁戊,乙丙丁,乙丙戊,乙丁戊,丙丁戊,而甲、乙都当选的包含3个样本点,故所求的概率为 P(A)= .
C
练习3:有五根细木棒,长度分别为1,3,5,7,9(cm),从中任取三根,能搭成三角形的概率是( )
A. B. C. D.
解析:设取出的三根木棒能搭成三角形为事件A,试验的样本空间Ω={(1,3,5), (1,3,7),(1,3,9),(1,5,7), (1,5,9), (1,7,9), (3,5,7),(3,5,9),(3,7,9),(5,7,9)},样本点的总数为10,由于三角形两边之和大于第三边,构成三角形的样本点只有(3,5,7), (3,7,9),(5,7,9)三种情况,故所求概率
为P(A)=
D
例四:如图所示,靶子由一个中心圆面Ⅰ和两个同心圆环Ⅱ、Ⅲ构成,射手命中Ⅰ、Ⅱ、Ⅲ的概率分别为0.35,0.30,0.25,则命不中靶的概率是______.
解析:“射手命中圆面Ⅰ”为事件A,“命中圆环Ⅱ”为事件B,“命中圆环Ⅲ”为事件C,“命不中靶”为事件D,则A,B,C彼此互斥,故射手中靶的概率为P(A∪B∪C)=P(A)+P(B)+P(C)=0.35+0.30+0.25=0.90.因为中靶和不中靶是对立事件,故命不中靶的概率为P(D)=1-P(A∪B∪C)=1-0.90=0.10.
0.1
例五:如图所示,A,B,C表示3个开关,若在某段时间内,它们正常工作的概率分别为0.9,0.8,0.7,则该系统的可靠性(3个开关只要一个开关正常工作即可靠)为( )
A.0.504 B.0.994
C.0.496 D.0.064
解析:记A,B,C正常工作为别为P(A),P(B),P(C),则P(A)=0.9, P(B)=0.8, P(C)=0.7由题意可知,三个开关工作与否相互独立,系统不可靠即为3个开关都不工作,
所以考虑对立事件,系统可靠性
1-(1-0.9)×(1-0.8)×(1-0.7)=1-0.006=0.994.
B
三、课堂小结
1、概率的基本性质
2、事件间的关系和运算
3、古典概型概率问题的求解
4、相互独立事件同时发生概率问题的求解
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
