人教A版必修二6.4.2向量在平面几何和物理的应用 课件(共22张PPT)
文档属性
| 名称 | 人教A版必修二6.4.2向量在平面几何和物理的应用 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 889.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-20 10:40:04 | ||
图片预览







文档简介
(共22张PPT)
平面向量的综合题
一.向量在平面几何中的向量方法
向量概念和运算,都有明确的物理背景和几何背景。
当向量与平面坐标系结合以后,向量的运算就可以转化为
“代数”的计算。
研究对象:
与向量有关的如距离、平行、三点共线、垂直、夹角等
几何问题。
例1
1.已知等腰△ABC,AB=AC,点M为边BC的中点,求证AM⊥BC.
1.利用向量的关系证明问题
通常先选取一组基底,基底中的向量最好已知模及两者之间的夹角,然后将问题中出现的向量用基底表示,再利用向量的运算法则、运算律以及一些重要性质运算,最后把运算结果还原为几何关系.
2.平面向量在坐标表示下的应用
利用平面向量的坐标表示,可以将平面几何中长度、垂直、平行等问题很容易地转化为代数运算的问题,运用此种方法必须建立适当的坐标系.
一.向量在平面几何中的向量方法
例2
答案:5
2.已知在直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=2,BC=1,
P是腰DC上的动点,则的最小值为 .
向量在物理中的应用
思考
1.两人一起提一个重物时,怎样提它最省力?
夹角越小越省力
2.一个人静止地垂挂在单杠上时,手臂的拉力与手臂握杠
的姿势有什么关系?
两臂的夹角越小,手臂就越省力
分析
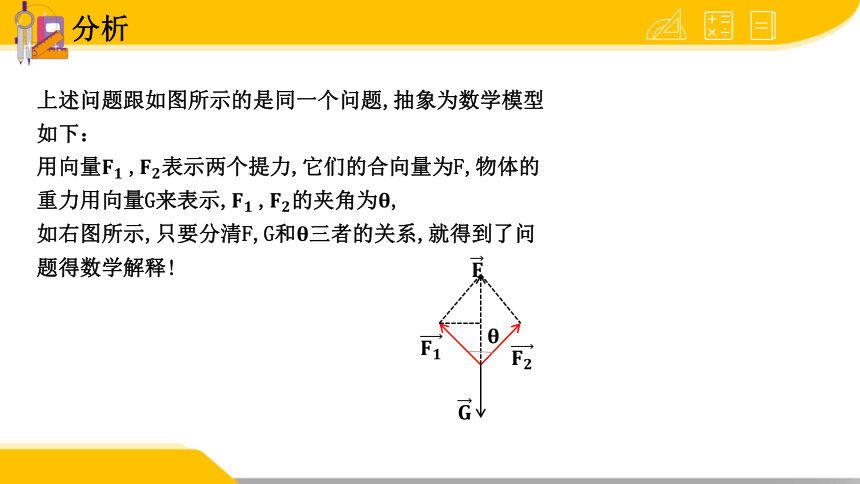
上述问题跟如图所示的是同一个问题,抽象为数学模型
如下:
用向量,表示两个提力,它们的合向量为F,物体的
重力用向量G来表示,,的夹角为,
如右图所示,只要分清F,G和三者的关系,就得到了问
题得数学解释!
证明
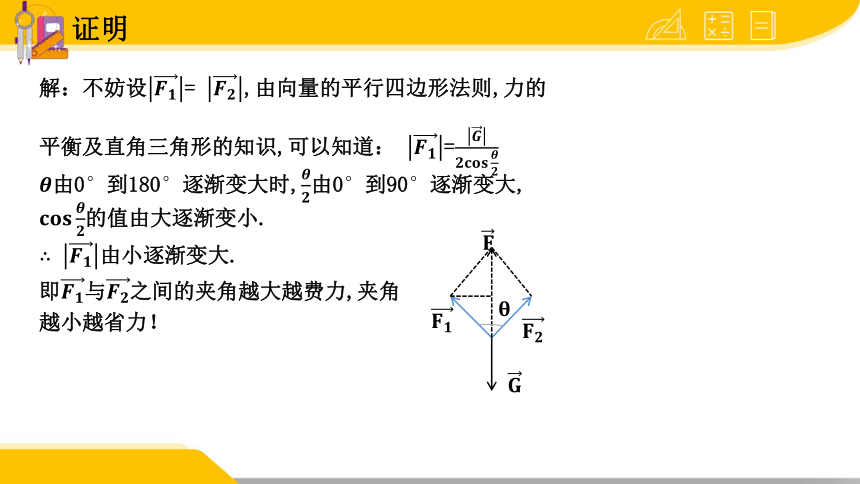
解:不妨设= ,由向量的平行四边形法则,力的
平衡及直角三角形的知识,可以知道: =
由0到180逐渐变大时,由到90逐渐变大,
的值由大逐渐变小.
由小逐渐变大.
即与之间的夹角越大越费力,夹角
越小越省力!
向量在物理中的应用
⑴问题的转化,即把物理问题转化为数学问题.
⑵模型的建立,即建立以向量为主题的数学模型,解决问
题.
⑶问题的答案,即回到问题的初始状态,解释相关的物理
现象.
例1
如图,一条河的两岸平行,河的宽度=500,一艘船从
A处出发到河对岸,已知船的速度=10/,水流速度
=2/,问
⑴行驶航程最短时,所用时间是多少?(精确到0.1min)
⑵行驶时间最短时,所用的时间是
多少?
分析:如图,已知
=+,=10/,
=2/, ,求t.
A
B
C
D
例1
解:由已知条件得=0
==
所以==603.1
答:行驶的航程最短时,所用的时间是3.1min.
A
B
例1
⑵小船过河的问题有一个特点,就是小船在垂直于河岸的
方向上的位移是不变的,我们只要在垂直于河岸方向上的
速度最大,小船过河所用的时间就最短,所以使小船垂直
于河岸方向行驶(小船自身的速度,方向指向河对岸),
小船过河所用时间才最短.
==60=3.
答:行驶的时间最短时,所用的时间是3min.
两向量的和与差的模的最值
PART
向量的三角不等式
01
向量的三角不等式
当向量、不共线时,和向量的长度与向量、的
长度和+,之间的大小关系如何?
当向量、不共线时,则 +
向量的三角不等式
当向量、共线时,它们之间又有什么关系呢?
若、方向相同时,则 = +
若、方向相反时,则 = -(或-)
综合以上探究得出的结论:
||+
(1)
(2)
A
B
C
A
C
B
向量的三角不等式
利用向量加法的三角不等式 +,能否推导出向量减法的不等式?
向量减法的不等式+
+
向量的三角不等式 +
例1
有下列不等式:
①-+②-== +
③-=+④-=+
其中,一定不成立的个数是( )
A.0 B.1 C.2 D.3
解析:选A ①当与不共线时成立;
②当=0,或=0,0时成立;
③当与共线,方向相反,且时成立;
④当与共线且方向相同时成立.
例2
若=2, =3,则的取值范围是( )
答案:[1,5]
变式:[1,5]
变式:求 的取值范围?
例3
若=8,=5,则的取值范围是( )
A.[3,8] B.(3,8)
C.[3,13] D.(3,13)
答案:C
下节课再见 谢谢!
平面向量的综合题
一.向量在平面几何中的向量方法
向量概念和运算,都有明确的物理背景和几何背景。
当向量与平面坐标系结合以后,向量的运算就可以转化为
“代数”的计算。
研究对象:
与向量有关的如距离、平行、三点共线、垂直、夹角等
几何问题。
例1
1.已知等腰△ABC,AB=AC,点M为边BC的中点,求证AM⊥BC.
1.利用向量的关系证明问题
通常先选取一组基底,基底中的向量最好已知模及两者之间的夹角,然后将问题中出现的向量用基底表示,再利用向量的运算法则、运算律以及一些重要性质运算,最后把运算结果还原为几何关系.
2.平面向量在坐标表示下的应用
利用平面向量的坐标表示,可以将平面几何中长度、垂直、平行等问题很容易地转化为代数运算的问题,运用此种方法必须建立适当的坐标系.
一.向量在平面几何中的向量方法
例2
答案:5
2.已知在直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=2,BC=1,
P是腰DC上的动点,则的最小值为 .
向量在物理中的应用
思考
1.两人一起提一个重物时,怎样提它最省力?
夹角越小越省力
2.一个人静止地垂挂在单杠上时,手臂的拉力与手臂握杠
的姿势有什么关系?
两臂的夹角越小,手臂就越省力
分析
上述问题跟如图所示的是同一个问题,抽象为数学模型
如下:
用向量,表示两个提力,它们的合向量为F,物体的
重力用向量G来表示,,的夹角为,
如右图所示,只要分清F,G和三者的关系,就得到了问
题得数学解释!
证明
解:不妨设= ,由向量的平行四边形法则,力的
平衡及直角三角形的知识,可以知道: =
由0到180逐渐变大时,由到90逐渐变大,
的值由大逐渐变小.
由小逐渐变大.
即与之间的夹角越大越费力,夹角
越小越省力!
向量在物理中的应用
⑴问题的转化,即把物理问题转化为数学问题.
⑵模型的建立,即建立以向量为主题的数学模型,解决问
题.
⑶问题的答案,即回到问题的初始状态,解释相关的物理
现象.
例1
如图,一条河的两岸平行,河的宽度=500,一艘船从
A处出发到河对岸,已知船的速度=10/,水流速度
=2/,问
⑴行驶航程最短时,所用时间是多少?(精确到0.1min)
⑵行驶时间最短时,所用的时间是
多少?
分析:如图,已知
=+,=10/,
=2/, ,求t.
A
B
C
D
例1
解:由已知条件得=0
==
所以==603.1
答:行驶的航程最短时,所用的时间是3.1min.
A
B
例1
⑵小船过河的问题有一个特点,就是小船在垂直于河岸的
方向上的位移是不变的,我们只要在垂直于河岸方向上的
速度最大,小船过河所用的时间就最短,所以使小船垂直
于河岸方向行驶(小船自身的速度,方向指向河对岸),
小船过河所用时间才最短.
==60=3.
答:行驶的时间最短时,所用的时间是3min.
两向量的和与差的模的最值
PART
向量的三角不等式
01
向量的三角不等式
当向量、不共线时,和向量的长度与向量、的
长度和+,之间的大小关系如何?
当向量、不共线时,则 +
向量的三角不等式
当向量、共线时,它们之间又有什么关系呢?
若、方向相同时,则 = +
若、方向相反时,则 = -(或-)
综合以上探究得出的结论:
||+
(1)
(2)
A
B
C
A
C
B
向量的三角不等式
利用向量加法的三角不等式 +,能否推导出向量减法的不等式?
向量减法的不等式+
+
向量的三角不等式 +
例1
有下列不等式:
①-+②-== +
③-=+④-=+
其中,一定不成立的个数是( )
A.0 B.1 C.2 D.3
解析:选A ①当与不共线时成立;
②当=0,或=0,0时成立;
③当与共线,方向相反,且时成立;
④当与共线且方向相同时成立.
例2
若=2, =3,则的取值范围是( )
答案:[1,5]
变式:[1,5]
变式:求 的取值范围?
例3
若=8,=5,则的取值范围是( )
A.[3,8] B.(3,8)
C.[3,13] D.(3,13)
答案:C
下节课再见 谢谢!
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
