4.5.3函数模型的应用 课件(共28张PPT)
文档属性
| 名称 | 4.5.3函数模型的应用 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-20 10:46:23 | ||
图片预览







文档简介
(共28张PPT)
4.5.3 函数模型的应用
常见函数模型
(1)一次函数模型:f(x)=kx+b(k,b为常数,k≠0);
(2)反比例函数模型:f(x)=+b(k,b为常数,k≠0);
(3)二次函数模型:f(x)=a+bx+c(a,b,c为常数,a≠0);
注意:二次函数模型是高中阶段应用最为广泛的模型,在高考的应用题考查中最为常见.
(4)指数函数模型:f(x)=a·+c(a,b,c为常数,a≠0,b>0,且b≠1);
(5)对数函数模型:f(x)=mx+n(m,n,a为常数,m≠0,a>0,且a≠1);
(6)幂函数模型:f(x)=a+b(a,b,n为常数,a≠0,n≠1);
(7)分段函数模型:这个模型实则是以上两种或多种模型的综合,因此应用也十分广泛.
我们知道 , 函数是描述客观世界变化规律的数学模型 , 不同的变化规律需要用不同的函数模型来刻画 . 面临一个实际问题 , 该如何选择恰当的函数模型来刻画它呢?
例3.人口问题是当今世界各国普遍关注的问题 . 认识人口数量的变化规律 , 可以为制定一系列相关政策提供依据 . 早在 1798 年 , 英国经济学家马尔萨斯 ( T.R.Malthas ,1766 — 1834) 就提出了自然状态下的人口增长模型 ,其中 t 表示经过的时间 , 表示 t=0 时的人口数 , r 表示人口的年平均增长率 .
(1) 根据国家统计网局网站公布的数据,我国1950年末、1959年末的人口总数分别为55196万和67207万。根据这些数据,用马尔萨斯人口增长模型建立我国在1951~1958年期间的具体人口增长模型。(2) 利用(1)中的模型计算1951~1958年各年末的人口总数。查阅国家统计局网站公布的我国在1951~1958年间各年末的实际人口数,检验所得模型与实际人口数据是否相符。(3)以(1)中的模型作预测,大约在什么时候我国人口总数达到13亿?
分析 : 用马尔萨斯人口增长模型 建立具体人口增长模型 , 就是要确定其中的初始量 和年平均增长率 r.
设1950~1959 年我国人口年平均增长率为 r ,
有67207=55196
由计算工具得我国1950年至1959年期间人口年平均增长率 r
我国1950年至1959年期间人口增长模型为
y=55196
,t
问题1:如何确定和r的值?
解:(1)由题意知=55196
问题2:如何检验所得模型与实际人口数据是否相符?
可以利用我们确定的人口增长模型求得我国各年末人口总数,再与国家统计局网站
公布的各年末的实际人口总数相比较检验所得模型与实际人口数据是否相符。
另一方面,我们也可以画出建立的函数模型的图象,并根据国家统计局网站公布的
各年末的实际人口总数数据画出散点图,通过图象观察所得模型与实际人口数据
是否相符。
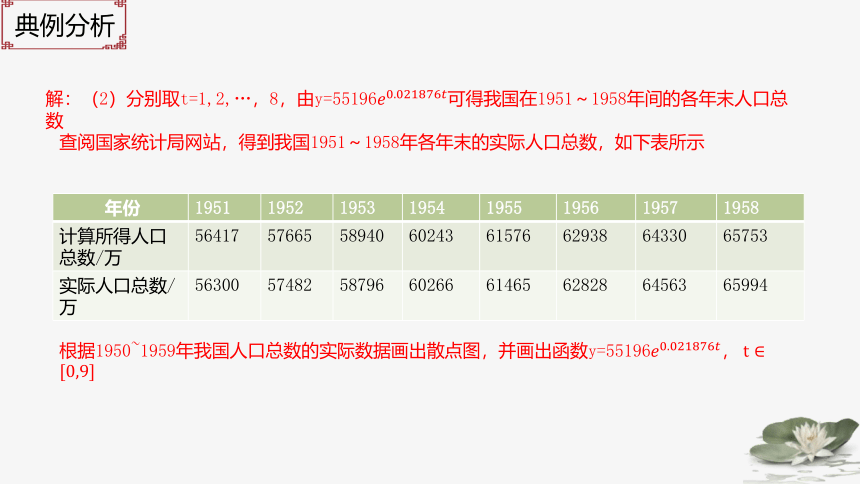
解:(2)分别取t=1,2,…,8,由y=551961951~1958年间的各年末人口总数
查阅国家统计局网站,得到我国1951~1958年各年末的实际人口总数,如下表所示
年份 1951 1952 1953 1954 1955 1956 1957 1958
计算所得人口总数/万 56417 57665 58940 60243 61576 62938 64330 65753
实际人口总数/万 56300 57482 58796 60266 61465 62828 64563 65994
根据1950~1959年我国人口总数的实际数据画出散点图,并画出函数y=55196
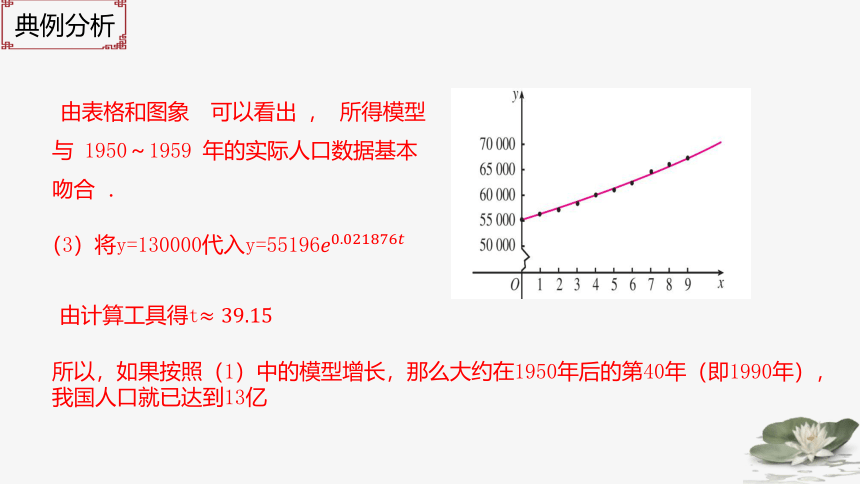
由表格和图象 可以看出 , 所得模型与 1950~1959 年的实际人口数据基本吻合 .
(3)将y=130000代入y=55196
由计算工具得t
所以,如果按照(1)中的模型增长,那么大约在1950年后的第40年(即1990年),
我国人口就已达到13亿
事实上 , 我国 1989年的人口数为 11.27亿 , 直到 2005年才突破13 亿 . 对由
函数模型所得的结果与实际情况不符 , 你有何看法 ?
因为人口基数较大 , 人口增长过快 , 与我国经济发展水平产生了较大矛盾 , 所以我国从 20 世纪 70 年代逐步实施了计划生育政策 . 因此这一阶段的人口增长条件并不符合马尔萨斯人口增长模型的条件 , 自然就出现了依模型得到的结果
与实际不符的情况 .
在利用已知的函数模型刻画实际问题时,应注意模型的适用条件
例4. 2010年 ,考古学家对良渚古城水利系统中一条水坝的建筑材料上提取的草茎遗存进行碳 14年代学检测 ,检测出碳 14的残留量约为初始量的 55.2% , 能否以此推断此水坝大概是什么年代建成的?
分析 : 因为死亡生物机体内碳 14 的初始量按确定的衰减率衰减 , 属于指数衰减 , 所以应选择函数( ∈R , 且 ≠0 ; >0 , 且 ≠1 ) 建立数学模型 .
解 : 设样本中碳 14 的初始量为k , 衰减率为 ( 0< <1 ),
经过 年后 , 残余量为 .
根据问题的实际意义 ,
( ∈R , 且 ≠0 ; 0< <1 ; ≥0 ) .
由碳 14 的半衰期为 5730年 , 得k=k
解得 .由计算工具得 ≈4912.
于是 ,所以
由样本中碳14 的残余量约为初始量的 55.2% 可知 ,即 0.552k
因为 2010年之前的 4912年是公元前 2903年 ,
所以推断此水坝大概是公元前 2903年建成的 .
当堂练习:课本150页练习1、2、3
利用已知函数模型解决实际问题,往往给出的函数解析式含有参数,需要将题中的数据代入函数模型,求得函数模型,并将所得模型用于解决有关实际问题。
例5.假设你有一笔资金用于投资,现有三种投资方案供你选择,
这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多回报10元;
方案三:第一天回报0.4元,以后每天的回报比前一天翻一番。
请问,你会选择哪种投资方案?
投资天数、回报金额
日 回 报
累计回报
分析:我们可以先建立三种投资方案所对应的函数模型,再通过比较它们的增长情况,
为选择投资方案提供依据
①问题中涉及哪些数量关系?
②如何用函数描述这些数量关系?
40
40
40
40
40
10
10+10
=10×2
10+10+10
=10×3
10+10+10+10
=10×4
10+10+10+10+10
=10×5
0.4
0.4×2
0.4×2×2
=0.4×22
0.4×2×2×2
=0.4×23
0.4×2×2×2×2
=0.4×24
方案一
方案二
方案三
1
2
3
4
5
则方案一可以用函数________________进行描述;
方案二可以用函数__________________描述;
方案三可以用函数______________________描述。
设第x天的回报是y元,
y=40 (x∈N*)
y=10x (x∈N*)
y=0.4×2x-1 (x∈N*)
三种方案每天回报表
x/天 方案1 方案2 方案3
y/元 增加量/元 y/元 增加量/元 y/元 增加量/元
1 40 10 0.4
2 40 0 20 10 0.8 0.4
3 40 0 30 10 1.6 0.8
4 40 0 40 10 3.2 1.6
5 40 0 50 10 6.4 3.2
6 40 0 60 10 12.8 6.4
7 40 0 70 10 25.6 12.8
8 40 0 80 10 51.2 25.6
9 40 0 90 10 102.4 51.2
10 40 0 100 10 204.8 102.4
… … … … … … …
30 40 0 300 10 21474836.8 107374182.4
o
x
y
20
40
60
80
100
120
140
4
2
6
8
10
12
我们看到,底为2的指数函数模型比线性函数模型增长速度要快得多.从中你对“指数爆炸”的含义有什么新的理解?
根据图象,是否可以得出这样的结论:投资1~4天选择方案一,投资5~8天选方案二,投资8天以上选方案三?
1 2 3 4 5 6 7 8 9 10 11 … 30
方案一 40 80 120 160 200 240 280 320 360 400 440 … 1200
方案二 10 30 60 100 150 210 280 360 450 550 660 … 4650
方案三 0 1 2.8 6 12 25 50.8 102 204 409 819 … 429496729.2
例5 累计回报表
投资1~6天,应选择方案一;
投资7天,应选择方案一或方案二;
投资8~10天,应选择方案二;
投资11天(含11天)以上,应选择方案三。
假如某公司每天给你投资1万元,共投资30天。公司要求你给他的回报是:第一天给公司1分钱,第二天给公司2分钱,以后每天给的钱都是前一天的2倍,共30天,你认为这样的交易对你有利吗?
你30天内给公司的回报为:
0.01+0.01×2+0.01×22+…+0.01×229
=10737418.23
≈1074(万元)
30万元
解答如下:公司30天内为你的总投资为:
上述例子只是一种假想情况 , 但从中可以看到 , 不同的函数增长模型 , 增长变化存在很大差异
例6. 某公司为了实现1000万元利润的目标,准备制定一个激励销售人员的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金y (单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不超过利润的25%。现有三个奖励模型:y=0.25x, y=log7x+1, y=1.002x,
其中哪个模型能符合公司的要求?
一次函数,
对数型函数,
指数函数。
①例6涉及了哪几类函数模型?
②如何检验以上模型是否符合公司要求
典例解析
Y≤5
且Y≤0.25X
所以只需检验当x[10 ,1000 ]时,是否满足
由于公司总的利润目标为 1000万元 , 所以销售人员的销售利润一般不会超过公司总的利润
不妨先画出函数图象 , 通过观察函数图象 , 得到初步的结论 , 再通过具体计算 , 确认结果 .
解 : 借助信息技术画出函数 y =5 , y=0.25x, y=log7x+1, y=1.002x 的图象. 观察图象发现 , 在区间 [ 10, 1000] 上 , 模型 y=0.25x, y=1.002x的图象都有一部分在直线 y =5 的上方 , 只有模型 y=log7x+1的图象始终在 y=5 的下方 , 这说明只有按模型 y=log7x+1进行奖励时才可能符合公司的要求 .
下面通过计算确认上述判断 .
先计算哪个模型的奖金总数不超过 5 万元 .
对于模型 y =0.25x, 它在区间 [ 10,1000 ] 上单调递增 ,
而且当 x =20 时 , y =5 ,
因此 , 当 x >20 时 , y >5 , 所以该模型不符合要求 ;
对于模型, y=1.002x , 由函数图象 ,
并利用信息技术 , 可知在区间 (805 ,806 )
内有一个点 满足 =5 , 由于它在区间 [10 ,1000 ] 上单调递增 ,
因此当 x> 时 , y >5 ,
所以该模型也不符合要求 ;
对于模型 y=log7x+1, 它在区间 [10 ,1000 ]上单调递增 , 而且当 x=1000 时 ,y=log71000+1≈4.55<5 ,
所以它符合奖金总数不超过 5 万元的要求 .
再计算按模型 y=log7x+1奖励时 , 奖金是否不超过利润的25% ,
即当 x ∈[10 ,1000 ] 时 , 是否有 y ≤0.25x,
即y=log7x+1 ≤0.25x成立 .
令 f(x) = y=log7x+1-0.25x, x ∈ [10 ,1000 ], 利用信息技术画出它的图象
由图象可知函数 f(x)在区间[10 ,1000 ] 上单调递减 ,
因此f(x)≤ f(10)≈-0.3167<0 ,
即y=log7x+1<0.25x.
所以 , 当 x ∈ [10 ,1000 ]时 ,
y ≤0.25x, 说明按模型y=log7x+1 奖励 ,
奖金不会超过利润的 25%.
综上所述 , 模型 y=log7x+1确实能符合公司要求 .
实际问题
数学建模的思路:
函数模型
化归
函数模型
检验和
完善模型
分析和
解决问题
运算
推理
解释说明
这一过程包括分析和理解实际问题的增长情况(是“对数增长”“直线升”还是“指数爆炸”),根据增长情况选择函数类型构建数学模型,将实际问题划归为数学问题;通过运算、推理求解函数模型,用得到的函数模型描述实际问题的变化规律,解决有关问题。
在这一过程中,往往需要利用信息技术帮助画图、运算等。
当堂练习:课本154页练习1、2
谢谢观看
4.5.3 函数模型的应用
常见函数模型
(1)一次函数模型:f(x)=kx+b(k,b为常数,k≠0);
(2)反比例函数模型:f(x)=+b(k,b为常数,k≠0);
(3)二次函数模型:f(x)=a+bx+c(a,b,c为常数,a≠0);
注意:二次函数模型是高中阶段应用最为广泛的模型,在高考的应用题考查中最为常见.
(4)指数函数模型:f(x)=a·+c(a,b,c为常数,a≠0,b>0,且b≠1);
(5)对数函数模型:f(x)=mx+n(m,n,a为常数,m≠0,a>0,且a≠1);
(6)幂函数模型:f(x)=a+b(a,b,n为常数,a≠0,n≠1);
(7)分段函数模型:这个模型实则是以上两种或多种模型的综合,因此应用也十分广泛.
我们知道 , 函数是描述客观世界变化规律的数学模型 , 不同的变化规律需要用不同的函数模型来刻画 . 面临一个实际问题 , 该如何选择恰当的函数模型来刻画它呢?
例3.人口问题是当今世界各国普遍关注的问题 . 认识人口数量的变化规律 , 可以为制定一系列相关政策提供依据 . 早在 1798 年 , 英国经济学家马尔萨斯 ( T.R.Malthas ,1766 — 1834) 就提出了自然状态下的人口增长模型 ,其中 t 表示经过的时间 , 表示 t=0 时的人口数 , r 表示人口的年平均增长率 .
(1) 根据国家统计网局网站公布的数据,我国1950年末、1959年末的人口总数分别为55196万和67207万。根据这些数据,用马尔萨斯人口增长模型建立我国在1951~1958年期间的具体人口增长模型。(2) 利用(1)中的模型计算1951~1958年各年末的人口总数。查阅国家统计局网站公布的我国在1951~1958年间各年末的实际人口数,检验所得模型与实际人口数据是否相符。(3)以(1)中的模型作预测,大约在什么时候我国人口总数达到13亿?
分析 : 用马尔萨斯人口增长模型 建立具体人口增长模型 , 就是要确定其中的初始量 和年平均增长率 r.
设1950~1959 年我国人口年平均增长率为 r ,
有67207=55196
由计算工具得我国1950年至1959年期间人口年平均增长率 r
我国1950年至1959年期间人口增长模型为
y=55196
,t
问题1:如何确定和r的值?
解:(1)由题意知=55196
问题2:如何检验所得模型与实际人口数据是否相符?
可以利用我们确定的人口增长模型求得我国各年末人口总数,再与国家统计局网站
公布的各年末的实际人口总数相比较检验所得模型与实际人口数据是否相符。
另一方面,我们也可以画出建立的函数模型的图象,并根据国家统计局网站公布的
各年末的实际人口总数数据画出散点图,通过图象观察所得模型与实际人口数据
是否相符。
解:(2)分别取t=1,2,…,8,由y=551961951~1958年间的各年末人口总数
查阅国家统计局网站,得到我国1951~1958年各年末的实际人口总数,如下表所示
年份 1951 1952 1953 1954 1955 1956 1957 1958
计算所得人口总数/万 56417 57665 58940 60243 61576 62938 64330 65753
实际人口总数/万 56300 57482 58796 60266 61465 62828 64563 65994
根据1950~1959年我国人口总数的实际数据画出散点图,并画出函数y=55196
由表格和图象 可以看出 , 所得模型与 1950~1959 年的实际人口数据基本吻合 .
(3)将y=130000代入y=55196
由计算工具得t
所以,如果按照(1)中的模型增长,那么大约在1950年后的第40年(即1990年),
我国人口就已达到13亿
事实上 , 我国 1989年的人口数为 11.27亿 , 直到 2005年才突破13 亿 . 对由
函数模型所得的结果与实际情况不符 , 你有何看法 ?
因为人口基数较大 , 人口增长过快 , 与我国经济发展水平产生了较大矛盾 , 所以我国从 20 世纪 70 年代逐步实施了计划生育政策 . 因此这一阶段的人口增长条件并不符合马尔萨斯人口增长模型的条件 , 自然就出现了依模型得到的结果
与实际不符的情况 .
在利用已知的函数模型刻画实际问题时,应注意模型的适用条件
例4. 2010年 ,考古学家对良渚古城水利系统中一条水坝的建筑材料上提取的草茎遗存进行碳 14年代学检测 ,检测出碳 14的残留量约为初始量的 55.2% , 能否以此推断此水坝大概是什么年代建成的?
分析 : 因为死亡生物机体内碳 14 的初始量按确定的衰减率衰减 , 属于指数衰减 , 所以应选择函数( ∈R , 且 ≠0 ; >0 , 且 ≠1 ) 建立数学模型 .
解 : 设样本中碳 14 的初始量为k , 衰减率为 ( 0< <1 ),
经过 年后 , 残余量为 .
根据问题的实际意义 ,
( ∈R , 且 ≠0 ; 0< <1 ; ≥0 ) .
由碳 14 的半衰期为 5730年 , 得k=k
解得 .由计算工具得 ≈4912.
于是 ,所以
由样本中碳14 的残余量约为初始量的 55.2% 可知 ,即 0.552k
因为 2010年之前的 4912年是公元前 2903年 ,
所以推断此水坝大概是公元前 2903年建成的 .
当堂练习:课本150页练习1、2、3
利用已知函数模型解决实际问题,往往给出的函数解析式含有参数,需要将题中的数据代入函数模型,求得函数模型,并将所得模型用于解决有关实际问题。
例5.假设你有一笔资金用于投资,现有三种投资方案供你选择,
这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多回报10元;
方案三:第一天回报0.4元,以后每天的回报比前一天翻一番。
请问,你会选择哪种投资方案?
投资天数、回报金额
日 回 报
累计回报
分析:我们可以先建立三种投资方案所对应的函数模型,再通过比较它们的增长情况,
为选择投资方案提供依据
①问题中涉及哪些数量关系?
②如何用函数描述这些数量关系?
40
40
40
40
40
10
10+10
=10×2
10+10+10
=10×3
10+10+10+10
=10×4
10+10+10+10+10
=10×5
0.4
0.4×2
0.4×2×2
=0.4×22
0.4×2×2×2
=0.4×23
0.4×2×2×2×2
=0.4×24
方案一
方案二
方案三
1
2
3
4
5
则方案一可以用函数________________进行描述;
方案二可以用函数__________________描述;
方案三可以用函数______________________描述。
设第x天的回报是y元,
y=40 (x∈N*)
y=10x (x∈N*)
y=0.4×2x-1 (x∈N*)
三种方案每天回报表
x/天 方案1 方案2 方案3
y/元 增加量/元 y/元 增加量/元 y/元 增加量/元
1 40 10 0.4
2 40 0 20 10 0.8 0.4
3 40 0 30 10 1.6 0.8
4 40 0 40 10 3.2 1.6
5 40 0 50 10 6.4 3.2
6 40 0 60 10 12.8 6.4
7 40 0 70 10 25.6 12.8
8 40 0 80 10 51.2 25.6
9 40 0 90 10 102.4 51.2
10 40 0 100 10 204.8 102.4
… … … … … … …
30 40 0 300 10 21474836.8 107374182.4
o
x
y
20
40
60
80
100
120
140
4
2
6
8
10
12
我们看到,底为2的指数函数模型比线性函数模型增长速度要快得多.从中你对“指数爆炸”的含义有什么新的理解?
根据图象,是否可以得出这样的结论:投资1~4天选择方案一,投资5~8天选方案二,投资8天以上选方案三?
1 2 3 4 5 6 7 8 9 10 11 … 30
方案一 40 80 120 160 200 240 280 320 360 400 440 … 1200
方案二 10 30 60 100 150 210 280 360 450 550 660 … 4650
方案三 0 1 2.8 6 12 25 50.8 102 204 409 819 … 429496729.2
例5 累计回报表
投资1~6天,应选择方案一;
投资7天,应选择方案一或方案二;
投资8~10天,应选择方案二;
投资11天(含11天)以上,应选择方案三。
假如某公司每天给你投资1万元,共投资30天。公司要求你给他的回报是:第一天给公司1分钱,第二天给公司2分钱,以后每天给的钱都是前一天的2倍,共30天,你认为这样的交易对你有利吗?
你30天内给公司的回报为:
0.01+0.01×2+0.01×22+…+0.01×229
=10737418.23
≈1074(万元)
30万元
解答如下:公司30天内为你的总投资为:
上述例子只是一种假想情况 , 但从中可以看到 , 不同的函数增长模型 , 增长变化存在很大差异
例6. 某公司为了实现1000万元利润的目标,准备制定一个激励销售人员的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金y (单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不超过利润的25%。现有三个奖励模型:y=0.25x, y=log7x+1, y=1.002x,
其中哪个模型能符合公司的要求?
一次函数,
对数型函数,
指数函数。
①例6涉及了哪几类函数模型?
②如何检验以上模型是否符合公司要求
典例解析
Y≤5
且Y≤0.25X
所以只需检验当x[10 ,1000 ]时,是否满足
由于公司总的利润目标为 1000万元 , 所以销售人员的销售利润一般不会超过公司总的利润
不妨先画出函数图象 , 通过观察函数图象 , 得到初步的结论 , 再通过具体计算 , 确认结果 .
解 : 借助信息技术画出函数 y =5 , y=0.25x, y=log7x+1, y=1.002x 的图象. 观察图象发现 , 在区间 [ 10, 1000] 上 , 模型 y=0.25x, y=1.002x的图象都有一部分在直线 y =5 的上方 , 只有模型 y=log7x+1的图象始终在 y=5 的下方 , 这说明只有按模型 y=log7x+1进行奖励时才可能符合公司的要求 .
下面通过计算确认上述判断 .
先计算哪个模型的奖金总数不超过 5 万元 .
对于模型 y =0.25x, 它在区间 [ 10,1000 ] 上单调递增 ,
而且当 x =20 时 , y =5 ,
因此 , 当 x >20 时 , y >5 , 所以该模型不符合要求 ;
对于模型, y=1.002x , 由函数图象 ,
并利用信息技术 , 可知在区间 (805 ,806 )
内有一个点 满足 =5 , 由于它在区间 [10 ,1000 ] 上单调递增 ,
因此当 x> 时 , y >5 ,
所以该模型也不符合要求 ;
对于模型 y=log7x+1, 它在区间 [10 ,1000 ]上单调递增 , 而且当 x=1000 时 ,y=log71000+1≈4.55<5 ,
所以它符合奖金总数不超过 5 万元的要求 .
再计算按模型 y=log7x+1奖励时 , 奖金是否不超过利润的25% ,
即当 x ∈[10 ,1000 ] 时 , 是否有 y ≤0.25x,
即y=log7x+1 ≤0.25x成立 .
令 f(x) = y=log7x+1-0.25x, x ∈ [10 ,1000 ], 利用信息技术画出它的图象
由图象可知函数 f(x)在区间[10 ,1000 ] 上单调递减 ,
因此f(x)≤ f(10)≈-0.3167<0 ,
即y=log7x+1<0.25x.
所以 , 当 x ∈ [10 ,1000 ]时 ,
y ≤0.25x, 说明按模型y=log7x+1 奖励 ,
奖金不会超过利润的 25%.
综上所述 , 模型 y=log7x+1确实能符合公司要求 .
实际问题
数学建模的思路:
函数模型
化归
函数模型
检验和
完善模型
分析和
解决问题
运算
推理
解释说明
这一过程包括分析和理解实际问题的增长情况(是“对数增长”“直线升”还是“指数爆炸”),根据增长情况选择函数类型构建数学模型,将实际问题划归为数学问题;通过运算、推理求解函数模型,用得到的函数模型描述实际问题的变化规律,解决有关问题。
在这一过程中,往往需要利用信息技术帮助画图、运算等。
当堂练习:课本154页练习1、2
谢谢观看
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
