4.5.1函数的零点与方程的解 课件(共21张PPT)
文档属性
| 名称 | 4.5.1函数的零点与方程的解 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-20 10:48:38 | ||
图片预览





文档简介
(共21张PPT)
4.5.1 函数零点与方程的解
4.5 函数的应用(二)
通过前面的学习,我们已经知道一元二次方程的实数根就是相应二次函数的零点
请你说出下列一元二次方程的根与相应的二次函数的零点:
(1)方程x2-2x-3=0与函数y=x2-2x-3
(2)方程x2-2x+1=0与函数y=x2-2x+1
(3)方程x2-2x+3=0与函数y=x2-2x+3
(2)
(3)
=-1,=3
x=1
方程无实根,对应函数也无零点
方程的根、函数的零点以及
函数图像与x轴的交点三者
之间有怎样的关系?
(1)
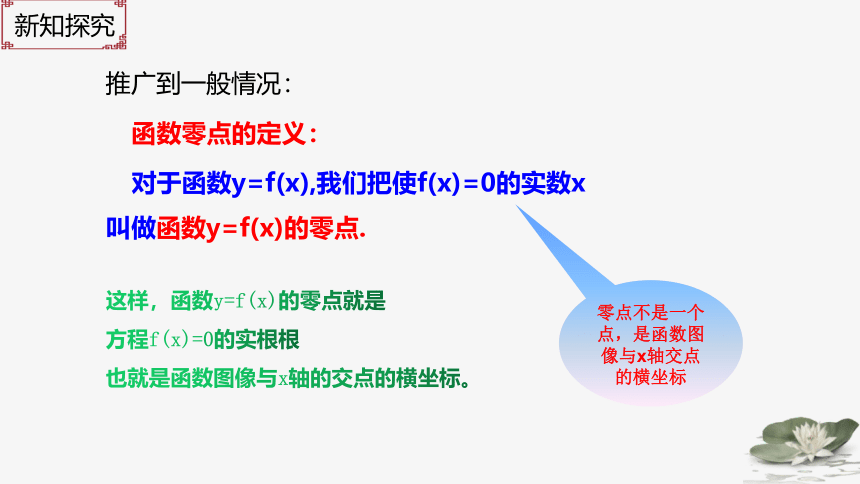
对于函数y=f(x),我们把使f(x)=0的实数x
叫做函数y=f(x)的零点.
函数零点的定义:
零点不是一个点,是函数图像与x轴交点的横坐标
推广到一般情况:
这样,函数y=f(x)的零点就是
方程f(x)=0的实根根
也就是函数图像与x轴的交点的横坐标。
方程f(x)=0有实数根
函数y=f(x)的图象与x轴有交点
函数y=f(x)有零点
由此可知,求方程f(x)=0的实数根,就是求函数y= f(x)的零点.对于不能用公式法求根的方程f(x)=0来说,可以将它与函数y=f(x)联系起来,利用函数的性质找出零点,从而求出方程的根.
思考:例如方程ln x +2x—6=0,我们如何利用函数y=ln +2x—6
的性质找出零点,从而求出方程的根呢?
为了回答以上问题,我们先从考察二次函数存在零点时零点附近的函数值的变化规律入手。
观察二次函数f(x)=x2-2x-3
的图象,我们发现它在区间[2,4]上有零点.这时,函数图象与x轴有什么关系?在区间[-2,0]上是否也具有这种关系?你认为应如何利用函数y=f(x)的取值规律来刻画这种关系?
再任意画几个函数的图象,观察函数零点所在区间,以及这一区间内函数图象与x轴的关系,并探究用f(x)的取值刻画这种关系的方法。
4
-1
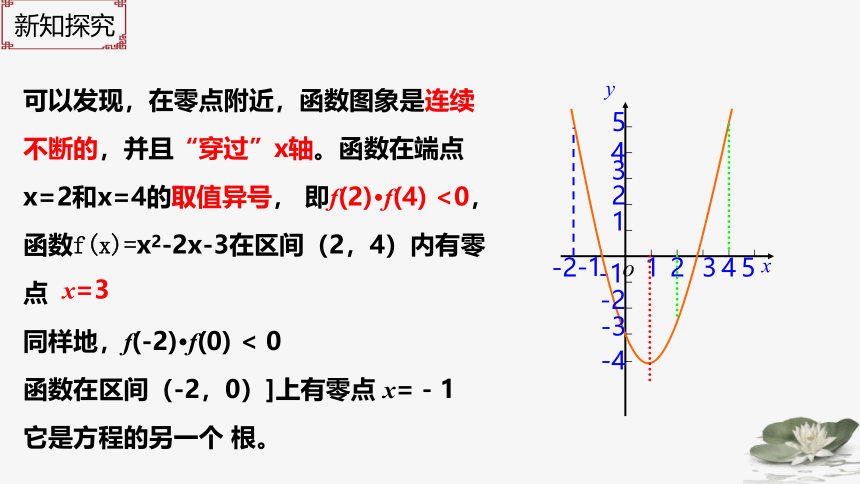
可以发现,在零点附近,函数图象是连续
不断的,并且“穿过”x轴。函数在端点x=2和x=4的取值异号, 即f(2)·f(4) <0, 函数f(x)=x2-2x-3在区间(2,4)内有零点
同样地,f(-2)·f(0) < 0
函数在区间(-2,0)]上有零点 x=-1
它是方程的另一个 根。
x=3
1
2
3
4
5
-1
-2
1
2
3
4
5
-2
-3
-4
x
y
x
y
O
a
b
c
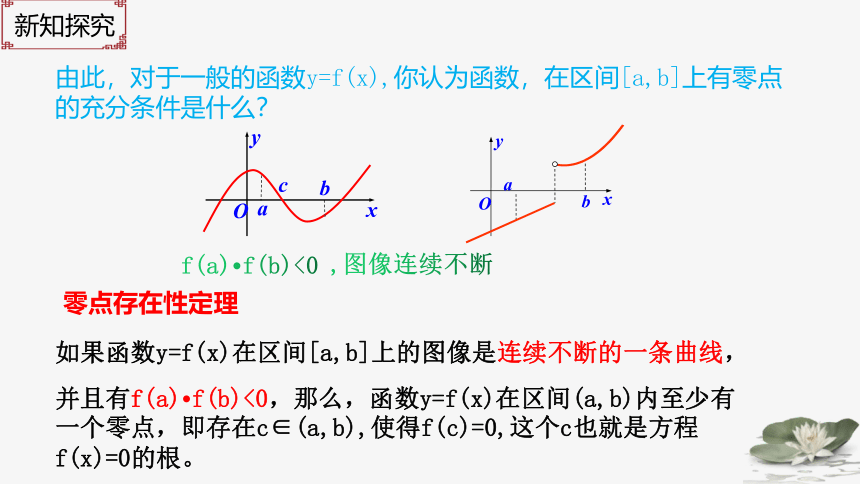
零点存在性定理
如果函数y=f(x)在区间[a,b]上的图像是连续不断的一条曲线,
并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b)内至少有一个零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根。
a
b
O
x
y
由此,对于一般的函数y=f(x),你认为函数,在区间[a,b]上有零点的充分条件是什么?
f(a)·f(b)<0
,图像连续不断
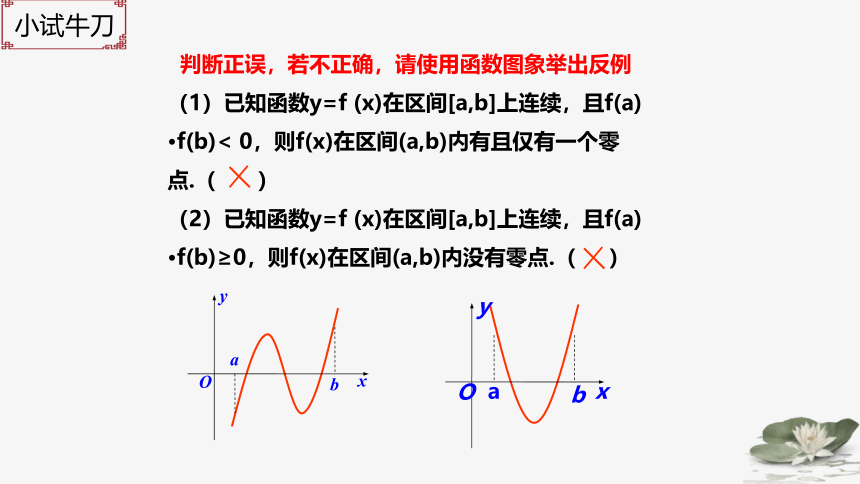
判断正误,若不正确,请使用函数图象举出反例
(1)已知函数y=f (x)在区间[a,b]上连续,且f(a)
·f(b)< 0,则f(x)在区间(a,b)内有且仅有一个零
点.( )
(2)已知函数y=f (x)在区间[a,b]上连续,且f(a)
·f(b)≥0,则f(x)在区间(a,b)内没有零点.( )
a
b
O
x
y
a
b
O
x
y
零点存在性定理的作用:
(1)可以判断零点所在的大致区间
(2)零点存在性定理 + 单调性,可以判断函数零点个数;
结论:如果函数y=f (x)在区间[a,b]上连续且单调,且f(a)
·f(b)< 0,则f(x)在区间(a,b)内有且仅有一个零
点.
由表可知f(2)<0,f(3)>0,
由于函数f(x)在定义域(0,+∞)内是增函数,所以它仅有一个零点.即方程lnx+2x-6=0只有一个实根。
用计算器或计算机作出x、f(x)的对应值表和图像;
例1.求方程lnx+2x-6=0解的个数.
解:
10
8
6
4
2
-2
-4
5
1
2
3
4
6
x
y
O
x 1 2 3 4 5 6 7 8 9
f(x)
-4
-1.3
1.1
3.4
5.6
7.8
9.9
12.1
14.2
方法一
f(x)=lnx+2x-6
从而f(2)·f(3)<0,∴函数f(x)在区间(2,3)内有零点.
y=-2x+6
y=lnx
6
O
x
1
2
3
4
y
求方程 lnx+2x-6=0的根的个数,即求 lnx=6-2x的根的个数,即判断函数y=lnx与函数y=6-2x的交点个数
如图可知,只有一个交点,即方程只有一根.
方法二:
判断方程f(x)=0实根个数的方法:
方法一、利用函数零点的存在性定理结合函数单调性判断;
方法二、将方程f(x)=0,通过移项变成 g1(x)=g2(x) 的形式,
进一步转化成两个函数图像的交点问题.
求方程x-2-x =0的根的个数,并确定根所在的区间[n,n+1](n∈Z).
解:求方程 x-2-x =0 的根的个数,即求方程
的根的个数,即判断函
数 与
的图象交点个数.由图可
知只有一解.
y=x
1
O
x
1
2
3
4
y
估算f(x)在各整数处的取值的正负:
令
由上表可知f(0)f(1)<0,方程的根所在区间为
x 0 1 2 3
f(x)
-
+
+
+
【答案】C
4.判断函数y=f(x)-g(x)零点个数的两种方法:
(1)零点存在性定理+单调性; (2)转化为方程f(x)-g(x)=0的实根个数,进而转化为函数y=f(x)与y=g(x)图像的交点个数。
谢谢观看
4.5.1 函数零点与方程的解
4.5 函数的应用(二)
通过前面的学习,我们已经知道一元二次方程的实数根就是相应二次函数的零点
请你说出下列一元二次方程的根与相应的二次函数的零点:
(1)方程x2-2x-3=0与函数y=x2-2x-3
(2)方程x2-2x+1=0与函数y=x2-2x+1
(3)方程x2-2x+3=0与函数y=x2-2x+3
(2)
(3)
=-1,=3
x=1
方程无实根,对应函数也无零点
方程的根、函数的零点以及
函数图像与x轴的交点三者
之间有怎样的关系?
(1)
对于函数y=f(x),我们把使f(x)=0的实数x
叫做函数y=f(x)的零点.
函数零点的定义:
零点不是一个点,是函数图像与x轴交点的横坐标
推广到一般情况:
这样,函数y=f(x)的零点就是
方程f(x)=0的实根根
也就是函数图像与x轴的交点的横坐标。
方程f(x)=0有实数根
函数y=f(x)的图象与x轴有交点
函数y=f(x)有零点
由此可知,求方程f(x)=0的实数根,就是求函数y= f(x)的零点.对于不能用公式法求根的方程f(x)=0来说,可以将它与函数y=f(x)联系起来,利用函数的性质找出零点,从而求出方程的根.
思考:例如方程ln x +2x—6=0,我们如何利用函数y=ln +2x—6
的性质找出零点,从而求出方程的根呢?
为了回答以上问题,我们先从考察二次函数存在零点时零点附近的函数值的变化规律入手。
观察二次函数f(x)=x2-2x-3
的图象,我们发现它在区间[2,4]上有零点.这时,函数图象与x轴有什么关系?在区间[-2,0]上是否也具有这种关系?你认为应如何利用函数y=f(x)的取值规律来刻画这种关系?
再任意画几个函数的图象,观察函数零点所在区间,以及这一区间内函数图象与x轴的关系,并探究用f(x)的取值刻画这种关系的方法。
4
-1
可以发现,在零点附近,函数图象是连续
不断的,并且“穿过”x轴。函数在端点x=2和x=4的取值异号, 即f(2)·f(4) <0, 函数f(x)=x2-2x-3在区间(2,4)内有零点
同样地,f(-2)·f(0) < 0
函数在区间(-2,0)]上有零点 x=-1
它是方程的另一个 根。
x=3
1
2
3
4
5
-1
-2
1
2
3
4
5
-2
-3
-4
x
y
x
y
O
a
b
c
零点存在性定理
如果函数y=f(x)在区间[a,b]上的图像是连续不断的一条曲线,
并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b)内至少有一个零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根。
a
b
O
x
y
由此,对于一般的函数y=f(x),你认为函数,在区间[a,b]上有零点的充分条件是什么?
f(a)·f(b)<0
,图像连续不断
判断正误,若不正确,请使用函数图象举出反例
(1)已知函数y=f (x)在区间[a,b]上连续,且f(a)
·f(b)< 0,则f(x)在区间(a,b)内有且仅有一个零
点.( )
(2)已知函数y=f (x)在区间[a,b]上连续,且f(a)
·f(b)≥0,则f(x)在区间(a,b)内没有零点.( )
a
b
O
x
y
a
b
O
x
y
零点存在性定理的作用:
(1)可以判断零点所在的大致区间
(2)零点存在性定理 + 单调性,可以判断函数零点个数;
结论:如果函数y=f (x)在区间[a,b]上连续且单调,且f(a)
·f(b)< 0,则f(x)在区间(a,b)内有且仅有一个零
点.
由表可知f(2)<0,f(3)>0,
由于函数f(x)在定义域(0,+∞)内是增函数,所以它仅有一个零点.即方程lnx+2x-6=0只有一个实根。
用计算器或计算机作出x、f(x)的对应值表和图像;
例1.求方程lnx+2x-6=0解的个数.
解:
10
8
6
4
2
-2
-4
5
1
2
3
4
6
x
y
O
x 1 2 3 4 5 6 7 8 9
f(x)
-4
-1.3
1.1
3.4
5.6
7.8
9.9
12.1
14.2
方法一
f(x)=lnx+2x-6
从而f(2)·f(3)<0,∴函数f(x)在区间(2,3)内有零点.
y=-2x+6
y=lnx
6
O
x
1
2
3
4
y
求方程 lnx+2x-6=0的根的个数,即求 lnx=6-2x的根的个数,即判断函数y=lnx与函数y=6-2x的交点个数
如图可知,只有一个交点,即方程只有一根.
方法二:
判断方程f(x)=0实根个数的方法:
方法一、利用函数零点的存在性定理结合函数单调性判断;
方法二、将方程f(x)=0,通过移项变成 g1(x)=g2(x) 的形式,
进一步转化成两个函数图像的交点问题.
求方程x-2-x =0的根的个数,并确定根所在的区间[n,n+1](n∈Z).
解:求方程 x-2-x =0 的根的个数,即求方程
的根的个数,即判断函
数 与
的图象交点个数.由图可
知只有一解.
y=x
1
O
x
1
2
3
4
y
估算f(x)在各整数处的取值的正负:
令
由上表可知f(0)f(1)<0,方程的根所在区间为
x 0 1 2 3
f(x)
-
+
+
+
【答案】C
4.判断函数y=f(x)-g(x)零点个数的两种方法:
(1)零点存在性定理+单调性; (2)转化为方程f(x)-g(x)=0的实根个数,进而转化为函数y=f(x)与y=g(x)图像的交点个数。
谢谢观看
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
