4.4.2对数函数的图像和性质 课件(共30张PPT)
文档属性
| 名称 | 4.4.2对数函数的图像和性质 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-20 10:50:40 | ||
图片预览











文档简介
(共30张PPT)
4.4.2 对数函数的图像与性质
1. 指数函数概念:
2. 指数函数的图像与性质:
形如y = ax(a 0,且a 1)的函数叫做指数函数.
(2)在R上是减函数
(1)过定点(0,1),即x=0时,y=1
性质
(0,+∞)
值域
R
定义域
图象
a>1
0(2)在R上是增函数
对数函数的特征:
1.底数:a>0,且a≠1
2.真数:自变量 x
3.系数:1
对数函数的概念:
一般地,函数y = logax ,(a>0,且a≠1) 叫做对数函数,其中x是自变量,
定义域是(0,+∞).
研究函数的一般方法:
背景
概念
图像与性质
应用
①定义域
②值域
③单调性
⑤奇偶性
④最值
与研究指数函数一样,我们首先画出其图像,然后借助图像研究其性质.请完成下列表格,并用描图法画出y = log2x的图像.
x y = log2x
0.5
1
2
4
6
8
16
-1
0
1
2
2.6
3
4
思考1:我们知道,底数互为倒数的两个指数函数的图象关于y轴对称.对于底数互为倒数的两个对数函数, 比如 和 ,它们的图象是否也有某种对称关系呢?可否利用其中一个函数的图象画出另一个函数的图象?
x
y
o
1
对数函数的图象
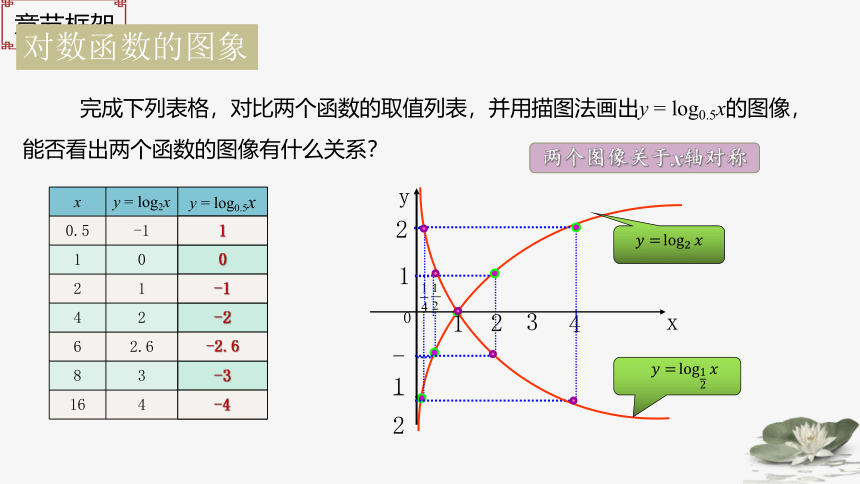
x y = log2x y = log0.5x
0.5 -1
1 0
2 1
4 2
6 2.6
8 3
16 4
完成下列表格,对比两个函数的取值列表,并用描图法画出y = log0.5x的图像,能否看出两个函数的图像有什么关系?
1
0
-1
-2
-2.6
-3
-4
两个图像关于x轴对称
2
1
-1
-2
1
2
4
0
y
x
3
即底数互为倒数的两个对数函数的图像关于x轴对称
探究1:选取底数a(a>0,且a)的若干不同的值,在同一直角坐标系内画出相应的对数函数的图像,观察这些图象的位置、公共点和变化趋势,它们有哪些共性?
发现对数函数y = logax 的图象按底数a的取值,可以分为01两种类型。
由此你能概括出y = logax (a>0,且a)的性质吗?
a>1 0<a<1
图象
y
X
O
x =1
(1,0)
y
X
O
x =1
(1,0)
性质
定义域为(0,+ ),值域为R.
过定点(1,0)即x=1时,y=0
在(0,+ )上是增函数
在(0,+ )上是减函数
当x>1时,y>0;
当0当x>1时, y<0;
当00
非奇非偶函数
对数函数的图象位置与底数的关系
作直线y=1与所给图象相交,交点的横坐标即为各个底数,根据在第一象限内,自左向右,对数函数的底数逐渐变大(底大图低)
练习1 函数y = logax,y = logbx,y = logcx,y = logdx的图像如图所示,则
a,b,c,d的大小关系为: .
【答案】b练习2 函数的 f (x)=loga(x-2)-2的图象必经过定点 .
【解析】令x-2=1,得x = 3,
所以f (3)=loga(3-2)-2=-2,
即函数的 f (x)=loga(x-2)-2的图象必经过定点(3,-2).
例3 比较下列各组中,两个值的大小:
(1) log23.4与 log28.5
(3) loga5.1与 loga5.9
(2) log 0.3 1.8与 log 0.3 2.7
(4)
(5)
例1 比较下列各组中,两个值的大小:
(1) log23.4与 log28.5
解:
考察函数y=log 2 x ,
∵a=2 > 1,
∴函数在区间(0,+∞)上是增函数;
∵3.4<8.5
∴ log23.4< log28.5
(2) log 0.3 1.8与 log 0.3 2.7
解:考察函数y=log 0.3 x ,
∵a=0.3< 1,
∴函数在区间(0,+∞)上是减函数;
∵1.8<2.7
∴ log 0.3 1.8> log 0.3 2.7
注意:若底数不确定,那就要对底数进行分类讨论
即0 1
(3) loga5.1与 loga5.9
解: ①若a>1则函数在区间(0,+∞)上是增函数;
∵5.1<5.9
∴ loga5.1 < loga5.9
②若0∴ loga5.1 > loga5.9
(4)
解:方法一:由于,,
又对数函数在上单 调递增,且
∴即.
在x=2时的两个函数值,结合图像可
知.
(5)
解:(中间值法)∵
∴.
(1)同底数比较大小时构造对数函数,根据其单调性比较.
(2)真数相同底数不同时分别画出不同底数的对数函数图象,当x取相同真数时可观察出函数值的大小.
(3)底数、真数都不相同时,借助中间0或1与两数比较.
(4)当底数含参数时,要按底数>1和0<<1两种情况分类讨论.
比较对数的大小的方法
2.比较下列各题中两个值的大小:
⑴ lg0.6 lg0.8
⑵ log0.56 log0.54
⑶ logm5 logm7
<
<
若a>1 则logm5 < logm7
若a<1 则logm5 >logm7
课本135 页第2题
【例2】溶液酸碱度是通过pH计量的. pH的计算公式为pH=-lg[H+],其中[H+]表示溶液中氢离子的浓度,单位是摩尔/升.
(1)根据对数函数性质及上述pH的计算公式,说明溶液酸碱度与溶液中氢离子的浓度之间的变化关系;
(2)已知纯净水中氢离子的浓度为[H+]=10-7摩尔/升,计算纯净水的pH.
(1)根据对数的运算性质, 有
在(0,+∞)上, 随着[H+]的增大,
pH减小.
∴随着[H+]的增大,
即pH减小.
即溶液中氢离子的浓度越大,溶液的酸性就越强.
解:
∴纯净水的pH是7.
相应地
探究2: 对于指数函数y=2x,你能利用指数与对数之间的关系,得到对应的对数函数?它们的定义域,值域有什么关系?
y=log2x
y = 2x
x= log 2 y
x改为y,
y改为x
x∈R
y∈(0,+∞)
x∈(0,+∞)
y∈R
一般地,函数y = log ax与y= ax (a>0,a≠1)互为反函数, 它们的定义域,值域互换,图象关于直线y=x对称。
log3.40.7, log0.60.8与 (
2.比较下面三个值的大小:
3.解不等式:
解:原不等式可化为:
图 象
性 质
对数函数y=log a x (a>0, a≠1)
指数函数y=ax (a>0,a≠1)
(4) a>1时, x<0,00,y>1
01;x>0,0(4) a>1时,01,y>0
00; x>1,y<0
(5) a>1时, 在R上是增函数;
0(5) a>1时,在(0,+∞)是增函数;
0(3)过点(0,1), 即x=0 时, y=1
(3)过点(1,0), 即x=1 时, y=0
(2)值域:(0,+∞)
(1)定义域:R
(1)定义域: (0,+∞)
(2)值域:R
y=ax
(a>1)
y=ax
(0x
y
o
1
y=logax
(a>1)
y=logax (0x
y
o
1
1.指数函数与对数函数的图象和性质
3.思想方法类比: 类比的思想方法:类比指数函数的研究方法;
数形结合思想方法:是研究函数图像和性质;
谢谢观看
4.4.2 对数函数的图像与性质
1. 指数函数概念:
2. 指数函数的图像与性质:
形如y = ax(a 0,且a 1)的函数叫做指数函数.
(2)在R上是减函数
(1)过定点(0,1),即x=0时,y=1
性质
(0,+∞)
值域
R
定义域
图象
a>1
0
对数函数的特征:
1.底数:a>0,且a≠1
2.真数:自变量 x
3.系数:1
对数函数的概念:
一般地,函数y = logax ,(a>0,且a≠1) 叫做对数函数,其中x是自变量,
定义域是(0,+∞).
研究函数的一般方法:
背景
概念
图像与性质
应用
①定义域
②值域
③单调性
⑤奇偶性
④最值
与研究指数函数一样,我们首先画出其图像,然后借助图像研究其性质.请完成下列表格,并用描图法画出y = log2x的图像.
x y = log2x
0.5
1
2
4
6
8
16
-1
0
1
2
2.6
3
4
思考1:我们知道,底数互为倒数的两个指数函数的图象关于y轴对称.对于底数互为倒数的两个对数函数, 比如 和 ,它们的图象是否也有某种对称关系呢?可否利用其中一个函数的图象画出另一个函数的图象?
x
y
o
1
对数函数的图象
x y = log2x y = log0.5x
0.5 -1
1 0
2 1
4 2
6 2.6
8 3
16 4
完成下列表格,对比两个函数的取值列表,并用描图法画出y = log0.5x的图像,能否看出两个函数的图像有什么关系?
1
0
-1
-2
-2.6
-3
-4
两个图像关于x轴对称
2
1
-1
-2
1
2
4
0
y
x
3
即底数互为倒数的两个对数函数的图像关于x轴对称
探究1:选取底数a(a>0,且a)的若干不同的值,在同一直角坐标系内画出相应的对数函数的图像,观察这些图象的位置、公共点和变化趋势,它们有哪些共性?
发现对数函数y = logax 的图象按底数a的取值,可以分为0
由此你能概括出y = logax (a>0,且a)的性质吗?
a>1 0<a<1
图象
y
X
O
x =1
(1,0)
y
X
O
x =1
(1,0)
性质
定义域为(0,+ ),值域为R.
过定点(1,0)即x=1时,y=0
在(0,+ )上是增函数
在(0,+ )上是减函数
当x>1时,y>0;
当0
当0
非奇非偶函数
对数函数的图象位置与底数的关系
作直线y=1与所给图象相交,交点的横坐标即为各个底数,根据在第一象限内,自左向右,对数函数的底数逐渐变大(底大图低)
练习1 函数y = logax,y = logbx,y = logcx,y = logdx的图像如图所示,则
a,b,c,d的大小关系为: .
【答案】b
【解析】令x-2=1,得x = 3,
所以f (3)=loga(3-2)-2=-2,
即函数的 f (x)=loga(x-2)-2的图象必经过定点(3,-2).
例3 比较下列各组中,两个值的大小:
(1) log23.4与 log28.5
(3) loga5.1与 loga5.9
(2) log 0.3 1.8与 log 0.3 2.7
(4)
(5)
例1 比较下列各组中,两个值的大小:
(1) log23.4与 log28.5
解:
考察函数y=log 2 x ,
∵a=2 > 1,
∴函数在区间(0,+∞)上是增函数;
∵3.4<8.5
∴ log23.4< log28.5
(2) log 0.3 1.8与 log 0.3 2.7
解:考察函数y=log 0.3 x ,
∵a=0.3< 1,
∴函数在区间(0,+∞)上是减函数;
∵1.8<2.7
∴ log 0.3 1.8> log 0.3 2.7
注意:若底数不确定,那就要对底数进行分类讨论
即0
(3) loga5.1与 loga5.9
解: ①若a>1则函数在区间(0,+∞)上是增函数;
∵5.1<5.9
∴ loga5.1 < loga5.9
②若0
(4)
解:方法一:由于,,
又对数函数在上单 调递增,且
∴即.
在x=2时的两个函数值,结合图像可
知.
(5)
解:(中间值法)∵
∴.
(1)同底数比较大小时构造对数函数,根据其单调性比较.
(2)真数相同底数不同时分别画出不同底数的对数函数图象,当x取相同真数时可观察出函数值的大小.
(3)底数、真数都不相同时,借助中间0或1与两数比较.
(4)当底数含参数时,要按底数>1和0<<1两种情况分类讨论.
比较对数的大小的方法
2.比较下列各题中两个值的大小:
⑴ lg0.6 lg0.8
⑵ log0.56 log0.54
⑶ logm5 logm7
<
<
若a>1 则logm5 < logm7
若a<1 则logm5 >logm7
课本135 页第2题
【例2】溶液酸碱度是通过pH计量的. pH的计算公式为pH=-lg[H+],其中[H+]表示溶液中氢离子的浓度,单位是摩尔/升.
(1)根据对数函数性质及上述pH的计算公式,说明溶液酸碱度与溶液中氢离子的浓度之间的变化关系;
(2)已知纯净水中氢离子的浓度为[H+]=10-7摩尔/升,计算纯净水的pH.
(1)根据对数的运算性质, 有
在(0,+∞)上, 随着[H+]的增大,
pH减小.
∴随着[H+]的增大,
即pH减小.
即溶液中氢离子的浓度越大,溶液的酸性就越强.
解:
∴纯净水的pH是7.
相应地
探究2: 对于指数函数y=2x,你能利用指数与对数之间的关系,得到对应的对数函数?它们的定义域,值域有什么关系?
y=log2x
y = 2x
x= log 2 y
x改为y,
y改为x
x∈R
y∈(0,+∞)
x∈(0,+∞)
y∈R
一般地,函数y = log ax与y= ax (a>0,a≠1)互为反函数, 它们的定义域,值域互换,图象关于直线y=x对称。
log3.40.7, log0.60.8与 (
2.比较下面三个值的大小:
3.解不等式:
解:原不等式可化为:
图 象
性 质
对数函数y=log a x (a>0, a≠1)
指数函数y=ax (a>0,a≠1)
(4) a>1时, x<0,0
0
0
(5) a>1时, 在R上是增函数;
0
0
(3)过点(1,0), 即x=1 时, y=0
(2)值域:(0,+∞)
(1)定义域:R
(1)定义域: (0,+∞)
(2)值域:R
y=ax
(a>1)
y=ax
(0
y
o
1
y=logax
(a>1)
y=logax (0
y
o
1
1.指数函数与对数函数的图象和性质
3.思想方法类比: 类比的思想方法:类比指数函数的研究方法;
数形结合思想方法:是研究函数图像和性质;
谢谢观看
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
