3.2 函数与方程、不等式之间关系 第1课时 课件(共19张PPT)
文档属性
| 名称 | 3.2 函数与方程、不等式之间关系 第1课时 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-20 10:52:03 | ||
图片预览





文档简介
(共19张PPT)
书 山 有 路 勤 为 径,学 海 无 崖 苦 作 舟
少 小 不 学 习,老 来 徒 伤 悲
成功=艰苦的劳动+正确的方法+少谈空话
天才就是百分之一的灵感,百分之九十九的汗水!
天 才 在 于 勤 奋,努 力 才 能 成 功!
勤劳的孩子展望未来, 但懒惰的孩子享受现在!!!
什 么 也 不 问 的 人 什 么 也 学 不 到 !!!
最可怕的事是同一起跑线上比你牛的人比你还努力
第三章 函数
3.2函数的零点三个二次问题
第一课时
学习目标
1.体会函数零点的概念以及函数零点与方程根的关系.
2.通过一元二次函数的零点问题解一元二次不等式.
3.了解高次不等式的解法.
引入
2、在图中作出函数 的图像,总结上述方程、不等式的解集与函数定义域、函数图像之间的关系。
函数值等于0
由
问题探究中的
例子可以看出
,
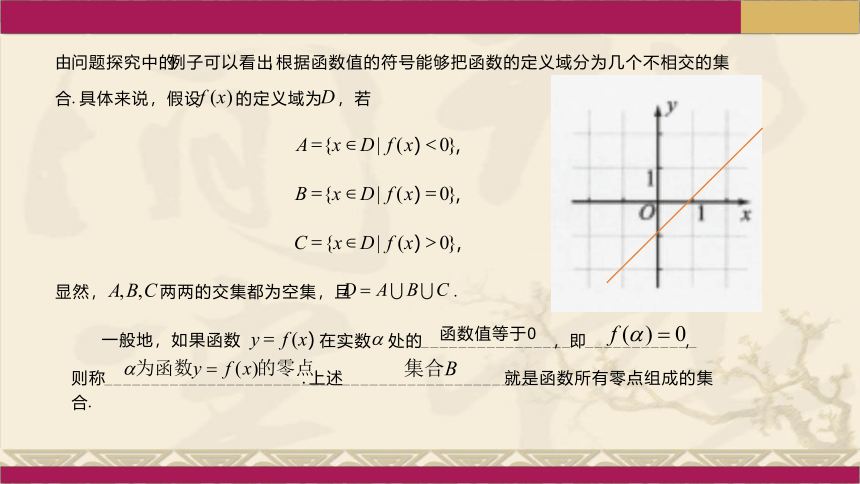
根据函数值的符号能够把函数的定义域分为几个不相交的集
合
.
具体来说,假设
)
(
x
f
的定义域为
D
,若
,
)
}
0
(
|
{
<
=
x
f
D
x
A
,
)
}
0
(
|
{
=
=
x
f
D
x
B
,
)
}
0
(
|
{
>
=
x
f
D
x
C
显然,
C
B
A
,
,
两两的交集都为空集,且
C
B
A
D
U
U
=
.
一般地,如果函数
)
x
f
y
(
=
在实数
a
处的
________________
,即
____________
,
则称
________________________
.
上述
____________________
就是函数所有零点组成的集
合
.
.
总结归纳
得到了这个方程的解集
函数图像与x轴的交点
函数的性质
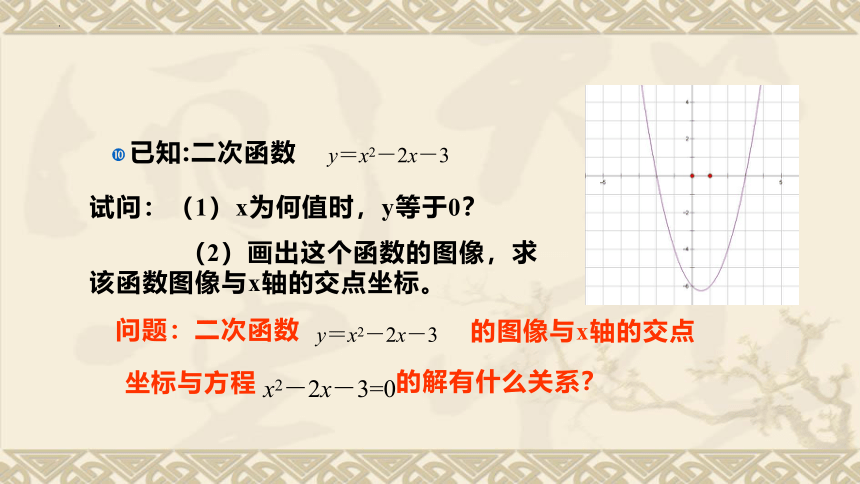
已知:二次函数
试问:(1)x为何值时,y等于0?
(2)画出这个函数的图像,求该函数图像与x轴的交点坐标。
问题:二次函数
的图像与x轴的交点
坐标与方程
的解有什么关系?
y=x2-2x-3
y=x2-2x-3
x2-2x-3=0
知识点二 二次函数的零点与对应方程、不等式解集之间的关系
函数 y=x2-2x-3 y=x2-2x+1 y=x2-2x+3
函数的图像
方程的实数根 ______________ x1=x2=1 _________
不等式的解集 y>0的解集___________ ___________ y>0的解集_________ ___________ y>0的解集__
y<0的解集_______ ____
x1=-1,x2=3
无实数根
(-∞,-1)
∪(3,+∞)
(-∞,1)
∪(1,+∞)
(-1,3)
R
1.所有的函数都有零点.( )
2.若方程f(x)=0有两个不等实根x1,x2,则函数y=f(x)的零点为(x1,0),(x2,0).
( )
3. 只有一个零点.( )
4.函数y=x3-16x的零点有3个.( )
×
×
×
√
题型二:一元二次不等式的解法
例2.利用函数求下列不等式的解集
例3.利用函数求下列不等式的解集
例4.利用函数求下列不等式的解集
0
-2
-1
1
观察图像在x轴上方和下方的情况
变式训练:
回顾本节课你有什么收获?
1.函数的零点定义
2.一元二次不等式的解法(步骤有哪些)
3.多项式函数的零点求法(穿根法)
书 山 有 路 勤 为 径,学 海 无 崖 苦 作 舟
少 小 不 学 习,老 来 徒 伤 悲
成功=艰苦的劳动+正确的方法+少谈空话
天才就是百分之一的灵感,百分之九十九的汗水!
天 才 在 于 勤 奋,努 力 才 能 成 功!
勤劳的孩子展望未来, 但懒惰的孩子享受现在!!!
什 么 也 不 问 的 人 什 么 也 学 不 到 !!!
最可怕的事是同一起跑线上比你牛的人比你还努力
第三章 函数
3.2函数的零点三个二次问题
第一课时
学习目标
1.体会函数零点的概念以及函数零点与方程根的关系.
2.通过一元二次函数的零点问题解一元二次不等式.
3.了解高次不等式的解法.
引入
2、在图中作出函数 的图像,总结上述方程、不等式的解集与函数定义域、函数图像之间的关系。
函数值等于0
由
问题探究中的
例子可以看出
,
根据函数值的符号能够把函数的定义域分为几个不相交的集
合
.
具体来说,假设
)
(
x
f
的定义域为
D
,若
,
)
}
0
(
|
{
<
=
x
f
D
x
A
,
)
}
0
(
|
{
=
=
x
f
D
x
B
,
)
}
0
(
|
{
>
=
x
f
D
x
C
显然,
C
B
A
,
,
两两的交集都为空集,且
C
B
A
D
U
U
=
.
一般地,如果函数
)
x
f
y
(
=
在实数
a
处的
________________
,即
____________
,
则称
________________________
.
上述
____________________
就是函数所有零点组成的集
合
.
.
总结归纳
得到了这个方程的解集
函数图像与x轴的交点
函数的性质
已知:二次函数
试问:(1)x为何值时,y等于0?
(2)画出这个函数的图像,求该函数图像与x轴的交点坐标。
问题:二次函数
的图像与x轴的交点
坐标与方程
的解有什么关系?
y=x2-2x-3
y=x2-2x-3
x2-2x-3=0
知识点二 二次函数的零点与对应方程、不等式解集之间的关系
函数 y=x2-2x-3 y=x2-2x+1 y=x2-2x+3
函数的图像
方程的实数根 ______________ x1=x2=1 _________
不等式的解集 y>0的解集___________ ___________ y>0的解集_________ ___________ y>0的解集__
y<0的解集_______ ____
x1=-1,x2=3
无实数根
(-∞,-1)
∪(3,+∞)
(-∞,1)
∪(1,+∞)
(-1,3)
R
1.所有的函数都有零点.( )
2.若方程f(x)=0有两个不等实根x1,x2,则函数y=f(x)的零点为(x1,0),(x2,0).
( )
3. 只有一个零点.( )
4.函数y=x3-16x的零点有3个.( )
×
×
×
√
题型二:一元二次不等式的解法
例2.利用函数求下列不等式的解集
例3.利用函数求下列不等式的解集
例4.利用函数求下列不等式的解集
0
-2
-1
1
观察图像在x轴上方和下方的情况
变式训练:
回顾本节课你有什么收获?
1.函数的零点定义
2.一元二次不等式的解法(步骤有哪些)
3.多项式函数的零点求法(穿根法)
