反比例函数回顾与思考

课件18张PPT。回顾与思考双流中学实验学校 陈苗温故而知新定义:一般地，如果两个变量x,y之间
的关系可以表示成： (K为常
数，K≠0）的形式，那么称y是x的
反比例函数.自变量x不能为０．
等价形式：(k≠0) y=kx-1xy=ky与x成反
比例小试牛刀
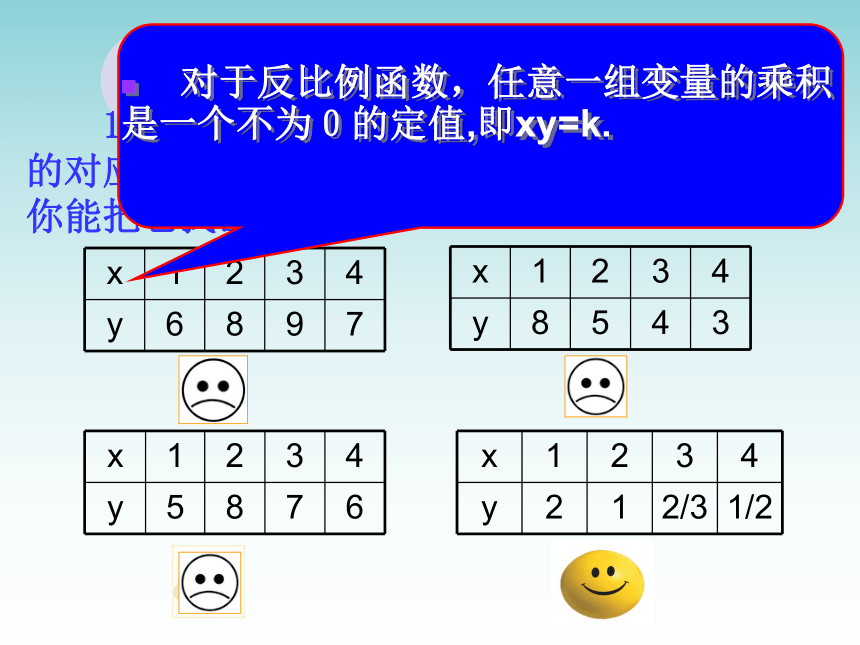
1.下列的数表中分别给出了变量y与x之间的对应关系，其中有一个表示的是反比例函数,你能把它找出来吗?(D) 对于反比例函数，任意一组变量的乘积是一个不为０的定值,即xy=k.
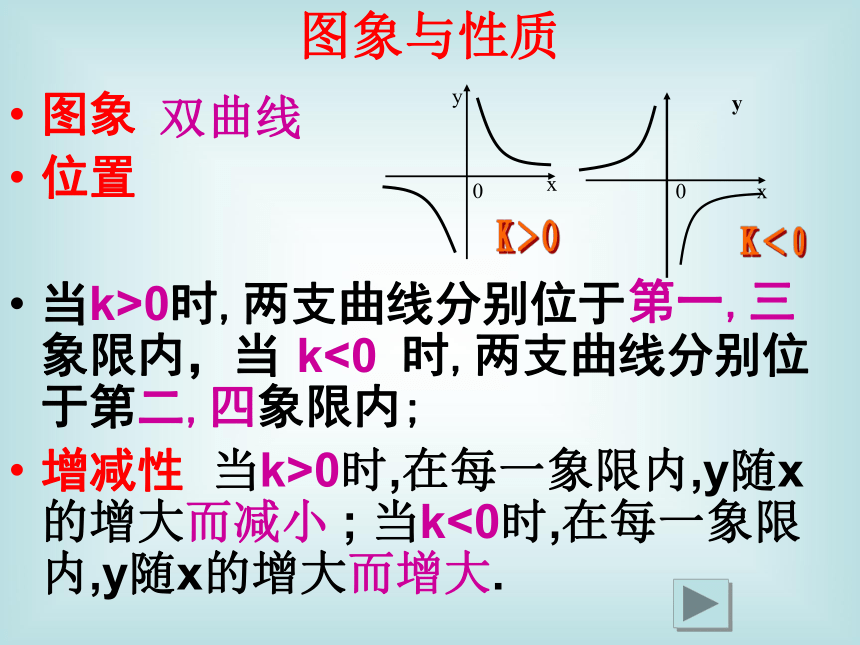
图象与性质图象
位置
当k>0时,两支曲线分别位于 　象限内，当 时,两支曲线分别位于第二,四象限内;
增减性 当k>0时,在每一象限内,y随x的增大而减小 ; 当k<0时,在每一象限内,y随x的增大而增大.双曲线第一,三k<00Ｋ＞ＯＫ＜０渐近性　反比例函数的图象无限接近于　　轴,但永远和坐标轴不相交．
对称性 反比例函数的图象是关于原点成 的图形.反比例函数的图象也是 　　图形.
“面积不变性”
　矩形面积 ︳xy︱＝︳K︱ 中心对称轴对称x,y １.已知函数 , 当x<0时,函数图象位于
第 象限。
２.已知反比例函数y=(m-2)x 的图象在每一象限内，y随x的增大而增大，求m的值．
解:由题意得　


三3.如图,点P是x轴上的一个动点,过点P作x轴的垂线PQ,交X轴于点Q,连结OP, 当点P沿x轴正半轴方向运动时,Rt△QOP面积( ) A.逐渐增大
B.逐渐减小
C.保持不变
D.无法确定xyoc考查面积不变性！SRt?QOP= ∣K ∣4、已知反比例函数 ,若
X1 （1）求反比例函数和一次函数的解析式；
（2）根据图象写出反比例函数的值大于一次函数的值的x的取值范围。N（-1，-4）M（2，m）（1）求反比例函数和一次函数的解析式；解:∵点N（-1，-4）在函数y＝　图象上
∴ -4= ,解得k=4, ∴y=
又∵点M（2，m）在函数y＝　图象上
∴m= ,得m=2 ∴Ｍ（2，2）
∵点M、N都在y=ax+b的图象上
∴ -4=-a+b
2=2a+b
∴解得a=2，b=-2
∴y= 2x-2yxN（-1，-4）M（2，m）解:观察图象得：
当x<-1或0　　　　过点Ｎ作y轴的垂线，垂足为点Ａ，若在y轴上有一点Ｂ，使得以Ｂ，Ｅ，Ｆ为顶点的三角形与?ＮＡＦ相似，求点Ｂ的坐标．yxM发散训练二Ｂ 谈谈本节的学习你有哪些收 获和体会,你学会了哪些数学思想和解题方法?学有所获★深刻体会数形结合、分类讨论及转化等数学思想在反比例函数问题中的应用；
★熟练掌握和运用待定系数法求函数解析式和图形分割法求面积；
★深刻理解反比例函数中∣Ｋ∣的几何意义,通常应将反比例函数知识和几何知识联系起来解决问题。
结束寄语