直线和圆的位置关系(福建省厦门市思明区)
文档属性
| 名称 | 直线和圆的位置关系(福建省厦门市思明区) |

|
|
| 格式 | rar | ||
| 文件大小 | 53.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-17 00:00:00 | ||
图片预览






文档简介
课件14张PPT。直线和圆的位置关系点和圆的位置关系有几种?
答:三种。点在圆外;点在圆上;点在圆内。复习提问如何判断点和圆的位置关系?
答:设点到圆的距离为d,圆半径为r.d > r ?点在圆外; d = r ?点在圆上;d < r ?点在圆内; 如果把点换成直线呢?
操作:
请同学们先画一个圆,再用直尺当直 线并任意移动,观察直线和圆的位置关系有几种?l直线和圆的位置关系思考:
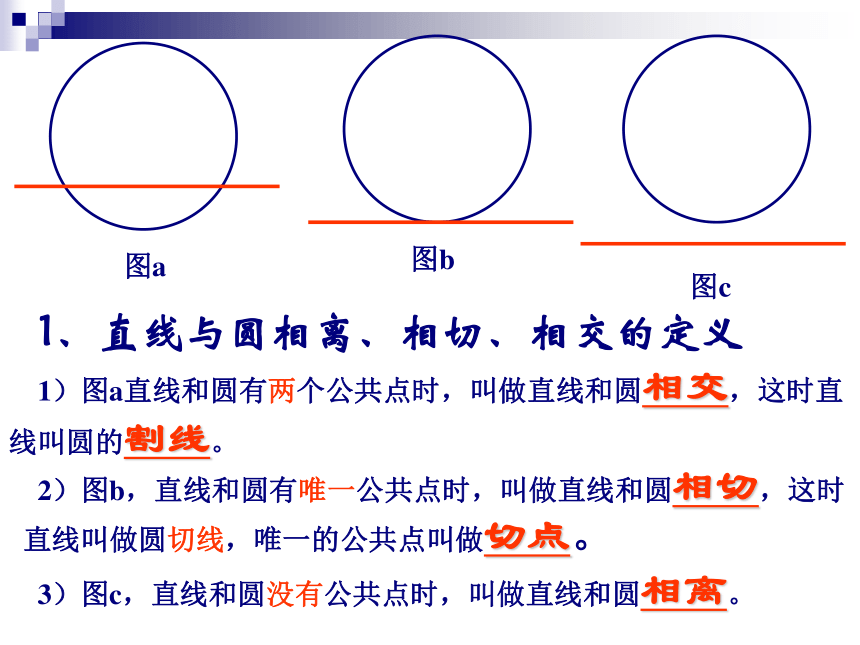
观察上图,直线与圆公共点个数有何特性?怎样定义这几种位置关系?图a图b图c1、直线与圆相离、相切、相交的定义 2)图b,直线和圆有唯一公共点时,叫做直线和圆相切,这时直线叫做圆切线,唯一的公共点叫做切点。3)图c,直线和圆没有公共点时,叫做直线和圆相离。 1)图a直线和圆有两个公共点时,叫做直线和圆相交,这时直线叫圆的割线。
1)直线和圆有公共点时叫做直线和圆相切,对吗?答:不对。应说为直线和圆有唯一公共点时,叫直线和圆相切2)如何判定点和圆的位置关系?答;设点到圆的距离为d,圆半径为r.d > r ?点在圆外; d = r ?点在圆上;d < r ?点在圆内;思考:
仿照点和圆位置关系的制定,怎样判断直线和圆的位置关系呢?
or???do?rdo?lllrd直线和圆的位置关系的判定 圆心到直线的距离与圆半径之间的数量关系,揭示直线和圆的位置关系。如果⊙O的半径为r,圆心O到直线l的距离为d那么1)直线l 和⊙O相交? d < r2)直线l 和⊙O相切? d = r 3)直线l 和⊙O相离? d > r3)研究直线和圆的位置关系,可以转化为点(圆心)到直线的距离与半径的大小关系。 说明:1)以上三条结论,既可以作为位置判定使用,又可以作为性质使用 2)以上三条结论左边反映的是两个图形(直线和圆)的位置关系,右边反映的是两个数量的大小关系。 例1:在Rt△ABC中,∠C=900,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?
1)r =2cm;2)r =2.4cm;3)r =3cm解:过C作CD⊥AB,垂足为D(如图),在Rt△ABC中,根据三角形的面积公式有 即圆心C到AB的距离d=2.4cm.D(1)当r =2cm时,有CD>r ,因此⊙C和AB相离(2)当r =2.4cm时,有CD=r ,因此⊙C和AB相切(3)当r =3cm时,有CD<r ,因此⊙C和AB相交 练习解答: 如图已知∠AOB=300,M为OB上一点,且OM=5cm,以M
为圆心,r为半径的圆 、和直线OA有怎样的位置关系?为什么?
(1)r =2cm;(2)r =4cm;(3)r =2.5cm。解:作MC⊥OA于C,
在Rt△OCM中,∠AOB=300即圆心M到OA的距离d=2.5cm(1)当r =2cm时,有d > r ,则OM与OA相离;
(2)当r =4cm时,有d < r ,则OM与OA相交;
(3)当r =2.5cm时,有d = r ,则OM与OA相切;300
小结:1、请同学们填写下表:相离 无d>r直线相切1个切点d=r切线相交2个交点d<r割线 本节主要学习了直线和圆的3种位置关系及直线与圆的位置关系的判定和性质 例2:正方形ABCD,边长为1,AC与BD交于O,过O作EF∥AB,分别交于AD、BC于E、F,以B为圆心, 为半径,则⊙B到直线AC、EF、DC的位置关系如何? 解:依题意知BO、BF、BC分别是点B到直线AC、EF、DC的距离。
在等腰Rt△ABO中,已知AB=1,
可得又依题意知: ∴以点B为圆心,为半径,分别与直线AC、EF、DC相切、相交、相离。 练习:如图∠BAC=900,D、E分别是BC和AC的中点,若AB=8cm,BC=10cm,则以点C为圆心,4.8cm为半径的圆与AB、AD、DE的位置关系如何?为什么? 解:Rt△ABC中AB=8,BC=10∴以点C为圆心,4.8cm为半径的圆与AB相离。∵AE=CE=3<4.8
∴DE∥AB,∴∠DEC=∠BAC=900,∴以点C为圆心,4.8cm为半径的圆
与DE相交。作CF⊥AD与F根据三角形的面积公式有 AD?CF=AC ?DE∴5×CF=6×4∴CF=4.8∴以点C为圆心,4.8cm为半径
的圆与AD相切∵BD=CD,
答:三种。点在圆外;点在圆上;点在圆内。复习提问如何判断点和圆的位置关系?
答:设点到圆的距离为d,圆半径为r.d > r ?点在圆外; d = r ?点在圆上;d < r ?点在圆内; 如果把点换成直线呢?
操作:
请同学们先画一个圆,再用直尺当直 线并任意移动,观察直线和圆的位置关系有几种?l直线和圆的位置关系思考:
观察上图,直线与圆公共点个数有何特性?怎样定义这几种位置关系?图a图b图c1、直线与圆相离、相切、相交的定义 2)图b,直线和圆有唯一公共点时,叫做直线和圆相切,这时直线叫做圆切线,唯一的公共点叫做切点。3)图c,直线和圆没有公共点时,叫做直线和圆相离。 1)图a直线和圆有两个公共点时,叫做直线和圆相交,这时直线叫圆的割线。
1)直线和圆有公共点时叫做直线和圆相切,对吗?答:不对。应说为直线和圆有唯一公共点时,叫直线和圆相切2)如何判定点和圆的位置关系?答;设点到圆的距离为d,圆半径为r.d > r ?点在圆外; d = r ?点在圆上;d < r ?点在圆内;思考:
仿照点和圆位置关系的制定,怎样判断直线和圆的位置关系呢?
or???do?rdo?lllrd直线和圆的位置关系的判定 圆心到直线的距离与圆半径之间的数量关系,揭示直线和圆的位置关系。如果⊙O的半径为r,圆心O到直线l的距离为d那么1)直线l 和⊙O相交? d < r2)直线l 和⊙O相切? d = r 3)直线l 和⊙O相离? d > r3)研究直线和圆的位置关系,可以转化为点(圆心)到直线的距离与半径的大小关系。 说明:1)以上三条结论,既可以作为位置判定使用,又可以作为性质使用 2)以上三条结论左边反映的是两个图形(直线和圆)的位置关系,右边反映的是两个数量的大小关系。 例1:在Rt△ABC中,∠C=900,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?
1)r =2cm;2)r =2.4cm;3)r =3cm解:过C作CD⊥AB,垂足为D(如图),在Rt△ABC中,根据三角形的面积公式有 即圆心C到AB的距离d=2.4cm.D(1)当r =2cm时,有CD>r ,因此⊙C和AB相离(2)当r =2.4cm时,有CD=r ,因此⊙C和AB相切(3)当r =3cm时,有CD<r ,因此⊙C和AB相交 练习解答: 如图已知∠AOB=300,M为OB上一点,且OM=5cm,以M
为圆心,r为半径的圆 、和直线OA有怎样的位置关系?为什么?
(1)r =2cm;(2)r =4cm;(3)r =2.5cm。解:作MC⊥OA于C,
在Rt△OCM中,∠AOB=300即圆心M到OA的距离d=2.5cm(1)当r =2cm时,有d > r ,则OM与OA相离;
(2)当r =4cm时,有d < r ,则OM与OA相交;
(3)当r =2.5cm时,有d = r ,则OM与OA相切;300
小结:1、请同学们填写下表:相离 无d>r直线相切1个切点d=r切线相交2个交点d<r割线 本节主要学习了直线和圆的3种位置关系及直线与圆的位置关系的判定和性质 例2:正方形ABCD,边长为1,AC与BD交于O,过O作EF∥AB,分别交于AD、BC于E、F,以B为圆心, 为半径,则⊙B到直线AC、EF、DC的位置关系如何? 解:依题意知BO、BF、BC分别是点B到直线AC、EF、DC的距离。
在等腰Rt△ABO中,已知AB=1,
可得又依题意知: ∴以点B为圆心,为半径,分别与直线AC、EF、DC相切、相交、相离。 练习:如图∠BAC=900,D、E分别是BC和AC的中点,若AB=8cm,BC=10cm,则以点C为圆心,4.8cm为半径的圆与AB、AD、DE的位置关系如何?为什么? 解:Rt△ABC中AB=8,BC=10∴以点C为圆心,4.8cm为半径的圆与AB相离。∵AE=CE=3<4.8
∴DE∥AB,∴∠DEC=∠BAC=900,∴以点C为圆心,4.8cm为半径的圆
与DE相交。作CF⊥AD与F根据三角形的面积公式有 AD?CF=AC ?DE∴5×CF=6×4∴CF=4.8∴以点C为圆心,4.8cm为半径
的圆与AD相切∵BD=CD,
