二次函数复习[下学期]

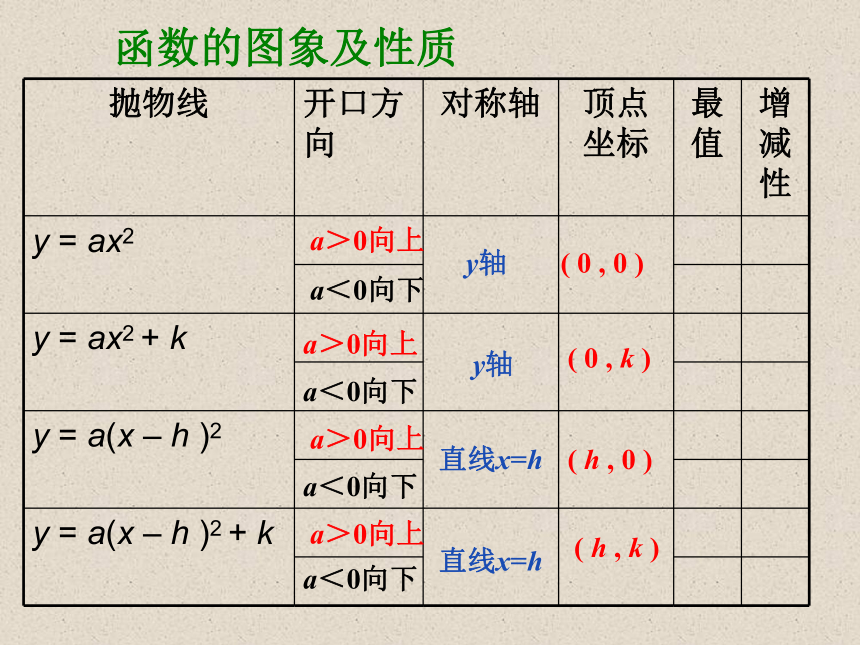
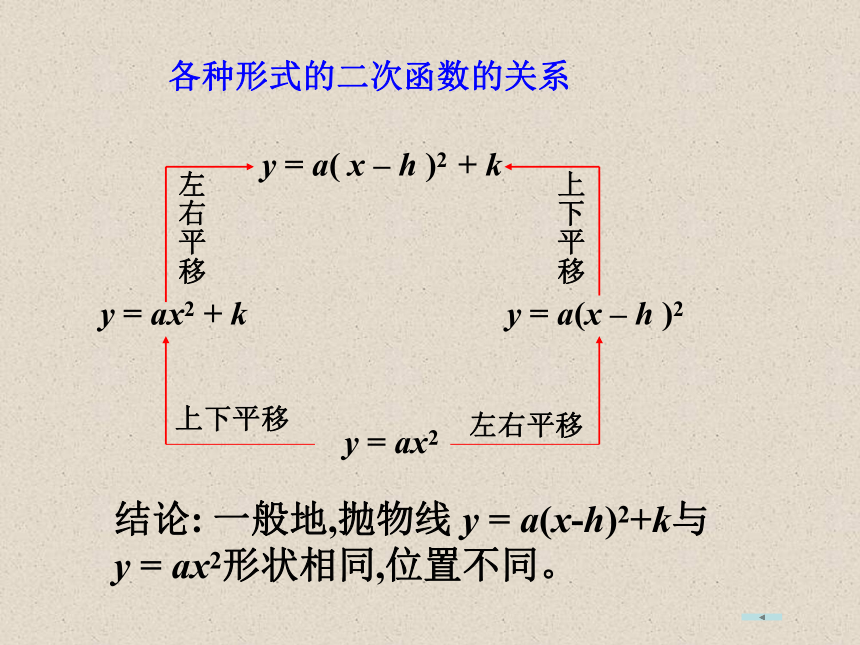
课件18张PPT。二次函数复习函数的图象及性质a＞0向上a＜0向下a＞0向上a＞0向上a＞0向上a＜0向下a＜0向下a＜0向下y轴直线x=h直线x=hy轴( 0 , 0 )( 0 , k )( h , 0 )( h , k )y = ax2y = ax2 + k y = a(x – h )2y = a( x – h )2 + k上下平移左右平移上下平移左右平移结论: 一般地,抛物线 y = a(x-h)2+k与y = ax2形状相同,位置不同。各种形式的二次函数的关系1、下列函数属于二次函数的是（ ）
A、 B、
C、 D、C2、抛物线 的顶点 （ ）
A、（2，1） B、（2，-1）
C、（-2，-1） D、（-2，1）CA变式：若抛物线为 ，则顶点坐标
为 。对称轴为 。3、将函数 进行配方，
正确的结果应 。（-1，4）直线x=-11.抛物线y=(x－3)2的开口方向 ,对称轴是 ，顶点坐标为 ，在对称轴左侧，即x 时，y随x增大而 ；在对称轴右侧，即x 时，y随x增大而 ，当x= 时，y有最 值为 .2.函数y=5(x－3)2－2的图象可由函数y=5x2的图象沿x轴向 平移 个单位，再沿y轴向 平移 个单位得到.3.二次函数y=a(x+k)2+k(a≠0)，无论k取什么实数，图象顶点必在（ ）.
A.直线y=-x上 B.x轴上 C.直线y=x上 D.y轴上4.若b<0，则函数y=2x2+bx－5的图象的顶点在（ ）
A.第一象限 B.第二象限 C.第三象限 D.第四象限5.设抛物线y=x2－4x+c的顶点在x轴上，则c为 . 6.二次函数y=ax2+bx+c经过点(3,6)和-1,6) ,则对称轴为 .7.如图，在同一坐标系中，函数y=ax+b与y=ax2+bx(ab≠0)的图象只可能是（ ）4、已知抛物线 经过点（-1，0），
则a-b+c= 。5、二次函数 的图象与x轴的两个交点坐标分别为（ ）
A、（0，0），（0，3）
B、（0，0），（3 ，0）
C、（0，0），（-3，0）
D、（0，0），（0，-3）0B变式：二次函数 的图象与x轴的交点坐标为 。6、抛物线 向左平移3个单位，
再向上平移1个单位得到的抛物线的
解析式是 。(4,0), (-1,0)7、写一个顶点为（-3，2），开口向下的
二次函数解析式 。><<< >10、二次函数 与x轴的
交点分别为A、B，与y轴的交点为C，
则的面积为 。X<1或x>46
二、1、设正方形边长是4，若边长增加x,则面积增加y.
(1)写出y与x的函数关系式。
（2）求当x=2时，y的值2、用30cm长的铁丝，折成一个矩形，设矩形的长为xcm,面积为ycm2.
(1)求y关于x的函数关系式；
（2）当x为多少cm时，y有最大值，其值为多少cm2 ？ 3、某旅行社组织团去外地旅游，30人起组团，每人单价800元，旅行社对超过30人的团给予优惠，即旅行团每增加一人，每人的单价就降低10元，你能帮助算一下，当一个旅行团的人数是多少时，旅行社可以获得最大的营业额？ 有一经销商，按市场价收购了一种活蟹1000千克，放养在塘内，此时市场价为每千克30元。据测算，此后每千克活蟹的市场价，每天可上升1元，但是，放养一天需各种费用支出400元，且平均每天还有10千克蟹死去，假定死蟹均于当天全部售出，售价都是每千克20元（放养期间蟹的重量不变）.
⑴设x天后每千克活蟹市场价为P元，写出P关于x的函数关系式.
⑵如果放养x天将活蟹一次性出售，并记1000千克蟹的销售总额为Q元，写出Q关于x的函数关系式。 ⑶该经销商将这批蟹放养多少天后出售，可获最大利润，（利润=销售总额-收购成本-费用）？最大利润是多少？
思考解：①由题意知:P=30+x.
②由题意知：死蟹的销售额为200x元，活蟹的销售额为（30+x）（1000-10x)元。
驶向胜利的彼岸∴Q=(30+x)(1000-10x)+200x
= -10x2+900x+30000③设总利润为W=Q-30000-400x=-10x2+500x =-10(x-25)2+6250
∴当x=25时，总利润最大，最大利润为6250元。
某新建商场设有百货部、服装部和家电部三个经营部，共有190名售货员，计划全商场日营业额(指每天卖出商品所收到的总金额)为60万元，由于营业性质不同，分配到三个部的售货员的人数也就不等，根据经验，各类商品每1万元营业额所需售货员人数如表（1），每1万元营业额所得利润情况如表（2）。商场将计划日营业额分配给三个经营部，设分配给百货部，服装部和家电部的营业额分别为x，y和z（单位：万元，x、y、z都是整数）。（1）请用含x的代数式分别表示y和z；（2）若商场预计每日的总利润为C（万元），且C满足19≤C≤19.7。问商场应如何分配营业额给三个经营部？各应分别安排多少名售货员？