青岛版数学八年级上册 2.6等腰三角形(3)等边三角形 课件(共21张PPT)
文档属性
| 名称 | 青岛版数学八年级上册 2.6等腰三角形(3)等边三角形 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 764.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-21 13:02:39 | ||
图片预览





文档简介
(共21张PPT)
2.6 等腰三角形
第3课时 等边三角形
学习目标
1.理解等腰三角形与等边三角形之间的关系,知道等边三角形具有等腰三角形的所有性质;
2.探索等边三角形的性质:等边三角形各角都等于60°;
3.掌握等边三角形的判定方法:三个角都相等的三角形是等边三角形;有一个角是60°的等腰三角形是等边三角形.
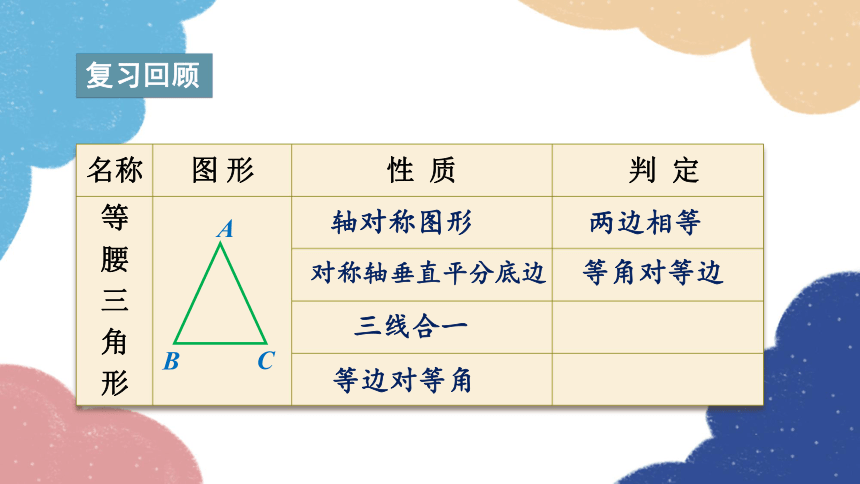
复习回顾
名称 图 形 性 质 判 定
等 腰 三 角 形
A
B
C
等角对等边
两边相等
轴对称图形
对称轴垂直平分底边
等边对等角
三线合一
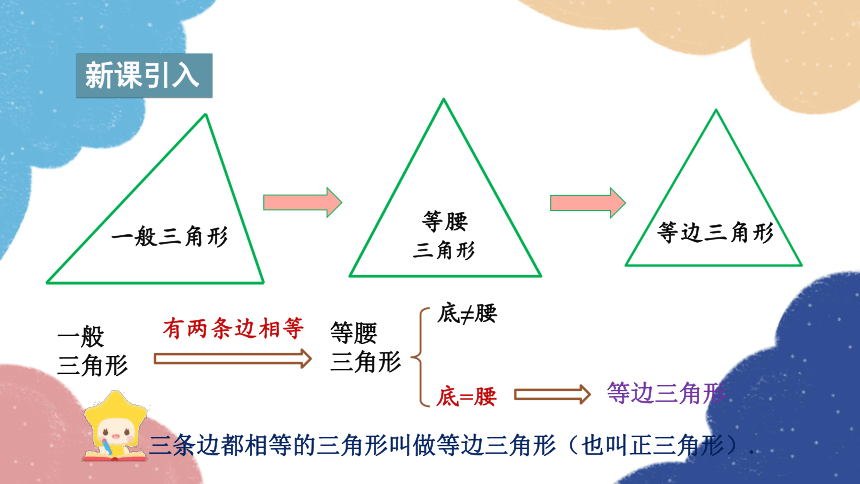
新课引入
一般三角形
等腰
三角形
一般
三角形
等腰
三角形
等边三角形
底≠腰
底=腰
有两条边相等
等边三角形
三条边都相等的三角形叫做等边三角形(也叫正三角形).
合作探究
思考:将等腰三角形的性质应用于等边三角形,能得到什么
结论呢?
小组合作,画出一个等边三角形,并用量角器量出每个内角的度数.
量角器量出每个内角都是60°.
猜想:等边三角形的各角都等于60°,运用等腰三角形的知识进行验证.
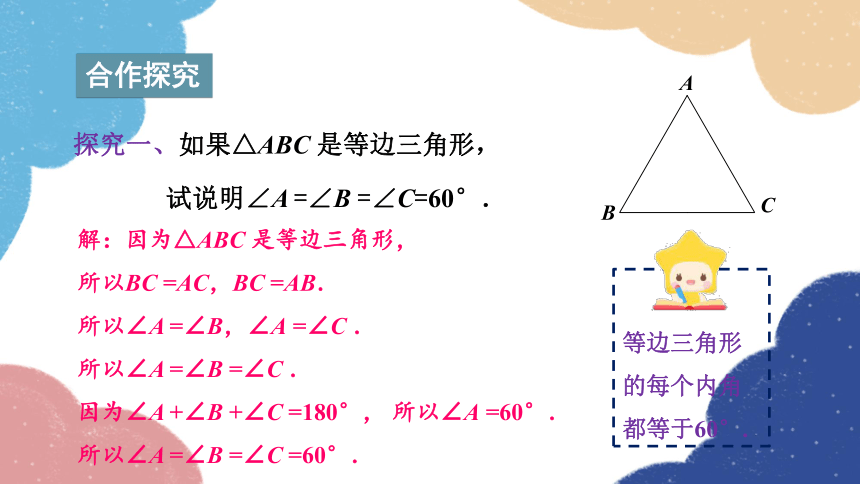
探究一、如果△ABC 是等边三角形,
试说明∠A =∠B =∠C=60°.
合作探究
A
B
C
解:因为△ABC 是等边三角形,
所以BC =AC,BC =AB.
所以∠A =∠B,∠A =∠C .
所以∠A =∠B =∠C .
因为∠A +∠B +∠C =180°, 所以∠A =60°.
所以∠A =∠B =∠C =60°.
等边三角形的每个内角都等于60°.
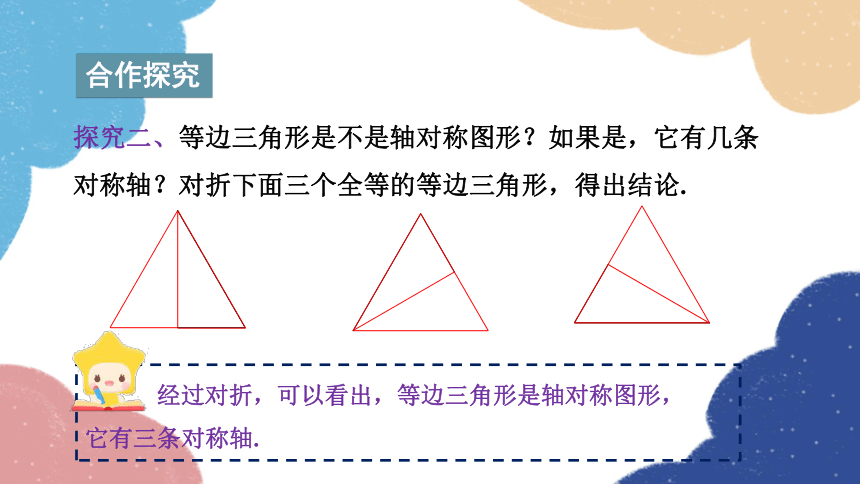
探究二、等边三角形是不是轴对称图形?如果是,它有几条对称轴?对折下面三个全等的等边三角形,得出结论.
合作探究
经过对折,可以看出,等边三角形是轴对称图形,
它有三条对称轴.
等边三角形的性质
一
1.等边三角形的各角都等于60°.
2.等边三角形是轴对称图形,它有三条对称轴.
3.等边三角形是特殊的等腰三角形,它具有等腰三角形的一切性质.
典例讲解
【例1】如图所示,P,Q是△ABC边BC上的两点,
且BP=PQ=QC=PA=AQ.求∠BAC的大小.
解:因为PA=PQ=AQ,所以△PAQ是等边三角形.
所以∠APQ=∠AQP=∠PAQ=60°.
因为PA=PB,所以∠B=∠PAB.
由三角形的外角性质,得∠B+∠PAB=∠APQ,所以∠B+∠PAB=60°,
所以∠B=∠PAB=30°,同理∠QAC=30°.
所以∠BAC=∠PAB+∠PAQ+∠QAC=30°+60°+30°=120°.
合作探究
探究三、满足什么条件的三角形是等边三角形呢?
可以类比等腰三角形的判定方法,
探究等边三角形的判定方法.
方法一:从边看
有两边相等的三角形是等腰三角形(定义).
三边都相等的三角形是等边三角形(定义).
方法一:
合作探究
探究三、满足什么条件的三角形是等边三角形呢?
可以类比等腰三角形的判定方法,
探究等边三角形的判定方法.
方法二:从角看
有两个角相等的三角形是等腰三角形.
三个角都相等的三角形是等边三角形.
方法二:
已知在△ABC 中,∠A=∠B=∠C.
那么△ABC 是等边三角形吗?
合作探究
A
B
C
解:因为∠A =∠B,∠B =∠C ,
所以BC =AC, AC =AB.
所以AB=BC =AC.
所以△ABC 是等边三角形.
探究四、有人认为还有第三种方法:“两条边相等且有一个角是60°的三角形也是等边三角形”,你同意吗?
合作探究
A
B
C
1.当顶角∠A=60°时,
∠B=∠C=60°,
所以∠A=∠B=∠C=60°,
所以△ABC是等边三角形.
2.当底角∠ B= 60°时, ∠C=60°,
∠A=180°-(60°+60°)=60°
所以∠A=∠B=∠C=60 °
所以△ABC是等边三角形.
若AB=AC,则∠B=∠C.
等边三角形的判定
二
1. 三条边都相等的三角形是等边三角形.
2.三个角都相等的三角形是等边三角形.
3.有一个内角为60°的等腰三角形是等边三角形.
典例讲解
【例2】△ABC是等边三角形,且∠1=∠2=∠3.
判断△DEF的形状,并简要说明理由.
A
B
C
F
D
E
1
2
3
分析:要判断△DEF的形状,可找出
△DEF三个内角的关系.由∠DFE是
△ACF的 角,得∠DFE=∠3+
,因为∠3=∠1,
所以∠DFE=∠1+________=_________= °,
同样地,得∠DEF=__________= °.
从而△DEF是_______三角形.
外
∠FAC
∠FAC
∠BAC
60
∠EDF
60
等边
典例讲解
【例2】△ABC是等边三角形,且∠1=∠2=∠3.
判断△DEF的形状,并简要说明理由.
A
B
C
F
D
E
1
2
3
解:△DEF是等边三角形.理由如下:
因为△ABC是等边三角形,
所以∠ABC=∠ACB=∠CAB=60°.
因为∠1=∠2=∠3,
所以∠DFE=∠3+∠FAC=∠1+∠FAC=∠CAB=60°.
同理∠DEF=∠EDF=60°.
所以△DEF是等边三角形.
课堂小结
等边三角形
性质
1.等边三角形的各角都等于60°.
2.等边三角形是轴对称图形,具有三条对称轴.
3.等边三角形具有等腰三角形的一切性质.
课堂小结
等边三角形
判定
1.三条边都相等的三角形是等边三角形.
2.三个角都相等的三角形是等边三角形.
3.有一个角是60°的等腰三角形是等边三角形.
已知三边关系,选用方法一;已知三角关系,选用方法二;
已知三角形是等腰三角形,选用方法三.
随堂训练
1.等边△ABC的两条角平分线BD和CE交于点I,则∠BIC等于( )
A.60° B.90°
C.120° D.150°
C
2.下列三角形:①有两个角等于60°;②有一个角等于60°的等腰三角形;③三个外角(每个顶点处各取一个外角)都相等的三角形;④一腰上的中线也是这条腰上的高的等腰三角形.其中是等边三角形的有( )
A.①②③ B.①②④ C.①③ D.①②③④
D
3.如图所示,在等边△ABC中,AB=3,∠ABC、∠ACB的平分线相交于点O,过O作OE∥AB,OF∥AC,交BC于点E、F,则△OEF的周长为 .
【解析】由于OB平分∠ABC,OE∥AB,可以得出OE=BE.同理可以得出OF=FC,因此△OEF的周长=OE+EF+OF=BE+EF+FC=BC=AB=3.
3
随堂训练
4.如图,D,E,F分别是等边△ABC三边上的点,且AD=BE=CF,
判断△DEF是等边三角形吗
解:因为△ABC是等边三角形,
所以∠A=∠B=∠C=60°, AB=BC=CA.
因为AD=BE=CF, 所以AF=BD=CE.
所以△ADF≌△BED≌△CFE.
所以DF=ED=FE.
所以△DEF是等边三角形.
随堂训练
2.6 等腰三角形
第3课时 等边三角形
学习目标
1.理解等腰三角形与等边三角形之间的关系,知道等边三角形具有等腰三角形的所有性质;
2.探索等边三角形的性质:等边三角形各角都等于60°;
3.掌握等边三角形的判定方法:三个角都相等的三角形是等边三角形;有一个角是60°的等腰三角形是等边三角形.
复习回顾
名称 图 形 性 质 判 定
等 腰 三 角 形
A
B
C
等角对等边
两边相等
轴对称图形
对称轴垂直平分底边
等边对等角
三线合一
新课引入
一般三角形
等腰
三角形
一般
三角形
等腰
三角形
等边三角形
底≠腰
底=腰
有两条边相等
等边三角形
三条边都相等的三角形叫做等边三角形(也叫正三角形).
合作探究
思考:将等腰三角形的性质应用于等边三角形,能得到什么
结论呢?
小组合作,画出一个等边三角形,并用量角器量出每个内角的度数.
量角器量出每个内角都是60°.
猜想:等边三角形的各角都等于60°,运用等腰三角形的知识进行验证.
探究一、如果△ABC 是等边三角形,
试说明∠A =∠B =∠C=60°.
合作探究
A
B
C
解:因为△ABC 是等边三角形,
所以BC =AC,BC =AB.
所以∠A =∠B,∠A =∠C .
所以∠A =∠B =∠C .
因为∠A +∠B +∠C =180°, 所以∠A =60°.
所以∠A =∠B =∠C =60°.
等边三角形的每个内角都等于60°.
探究二、等边三角形是不是轴对称图形?如果是,它有几条对称轴?对折下面三个全等的等边三角形,得出结论.
合作探究
经过对折,可以看出,等边三角形是轴对称图形,
它有三条对称轴.
等边三角形的性质
一
1.等边三角形的各角都等于60°.
2.等边三角形是轴对称图形,它有三条对称轴.
3.等边三角形是特殊的等腰三角形,它具有等腰三角形的一切性质.
典例讲解
【例1】如图所示,P,Q是△ABC边BC上的两点,
且BP=PQ=QC=PA=AQ.求∠BAC的大小.
解:因为PA=PQ=AQ,所以△PAQ是等边三角形.
所以∠APQ=∠AQP=∠PAQ=60°.
因为PA=PB,所以∠B=∠PAB.
由三角形的外角性质,得∠B+∠PAB=∠APQ,所以∠B+∠PAB=60°,
所以∠B=∠PAB=30°,同理∠QAC=30°.
所以∠BAC=∠PAB+∠PAQ+∠QAC=30°+60°+30°=120°.
合作探究
探究三、满足什么条件的三角形是等边三角形呢?
可以类比等腰三角形的判定方法,
探究等边三角形的判定方法.
方法一:从边看
有两边相等的三角形是等腰三角形(定义).
三边都相等的三角形是等边三角形(定义).
方法一:
合作探究
探究三、满足什么条件的三角形是等边三角形呢?
可以类比等腰三角形的判定方法,
探究等边三角形的判定方法.
方法二:从角看
有两个角相等的三角形是等腰三角形.
三个角都相等的三角形是等边三角形.
方法二:
已知在△ABC 中,∠A=∠B=∠C.
那么△ABC 是等边三角形吗?
合作探究
A
B
C
解:因为∠A =∠B,∠B =∠C ,
所以BC =AC, AC =AB.
所以AB=BC =AC.
所以△ABC 是等边三角形.
探究四、有人认为还有第三种方法:“两条边相等且有一个角是60°的三角形也是等边三角形”,你同意吗?
合作探究
A
B
C
1.当顶角∠A=60°时,
∠B=∠C=60°,
所以∠A=∠B=∠C=60°,
所以△ABC是等边三角形.
2.当底角∠ B= 60°时, ∠C=60°,
∠A=180°-(60°+60°)=60°
所以∠A=∠B=∠C=60 °
所以△ABC是等边三角形.
若AB=AC,则∠B=∠C.
等边三角形的判定
二
1. 三条边都相等的三角形是等边三角形.
2.三个角都相等的三角形是等边三角形.
3.有一个内角为60°的等腰三角形是等边三角形.
典例讲解
【例2】△ABC是等边三角形,且∠1=∠2=∠3.
判断△DEF的形状,并简要说明理由.
A
B
C
F
D
E
1
2
3
分析:要判断△DEF的形状,可找出
△DEF三个内角的关系.由∠DFE是
△ACF的 角,得∠DFE=∠3+
,因为∠3=∠1,
所以∠DFE=∠1+________=_________= °,
同样地,得∠DEF=__________= °.
从而△DEF是_______三角形.
外
∠FAC
∠FAC
∠BAC
60
∠EDF
60
等边
典例讲解
【例2】△ABC是等边三角形,且∠1=∠2=∠3.
判断△DEF的形状,并简要说明理由.
A
B
C
F
D
E
1
2
3
解:△DEF是等边三角形.理由如下:
因为△ABC是等边三角形,
所以∠ABC=∠ACB=∠CAB=60°.
因为∠1=∠2=∠3,
所以∠DFE=∠3+∠FAC=∠1+∠FAC=∠CAB=60°.
同理∠DEF=∠EDF=60°.
所以△DEF是等边三角形.
课堂小结
等边三角形
性质
1.等边三角形的各角都等于60°.
2.等边三角形是轴对称图形,具有三条对称轴.
3.等边三角形具有等腰三角形的一切性质.
课堂小结
等边三角形
判定
1.三条边都相等的三角形是等边三角形.
2.三个角都相等的三角形是等边三角形.
3.有一个角是60°的等腰三角形是等边三角形.
已知三边关系,选用方法一;已知三角关系,选用方法二;
已知三角形是等腰三角形,选用方法三.
随堂训练
1.等边△ABC的两条角平分线BD和CE交于点I,则∠BIC等于( )
A.60° B.90°
C.120° D.150°
C
2.下列三角形:①有两个角等于60°;②有一个角等于60°的等腰三角形;③三个外角(每个顶点处各取一个外角)都相等的三角形;④一腰上的中线也是这条腰上的高的等腰三角形.其中是等边三角形的有( )
A.①②③ B.①②④ C.①③ D.①②③④
D
3.如图所示,在等边△ABC中,AB=3,∠ABC、∠ACB的平分线相交于点O,过O作OE∥AB,OF∥AC,交BC于点E、F,则△OEF的周长为 .
【解析】由于OB平分∠ABC,OE∥AB,可以得出OE=BE.同理可以得出OF=FC,因此△OEF的周长=OE+EF+OF=BE+EF+FC=BC=AB=3.
3
随堂训练
4.如图,D,E,F分别是等边△ABC三边上的点,且AD=BE=CF,
判断△DEF是等边三角形吗
解:因为△ABC是等边三角形,
所以∠A=∠B=∠C=60°, AB=BC=CA.
因为AD=BE=CF, 所以AF=BD=CE.
所以△ADF≌△BED≌△CFE.
所以DF=ED=FE.
所以△DEF是等边三角形.
随堂训练
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
