人教版数学八年级上册 专题三 整式的乘法与因式分解 期末复习课件
文档属性
| 名称 | 人教版数学八年级上册 专题三 整式的乘法与因式分解 期末复习课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-21 13:05:16 | ||
图片预览








文档简介
(共24张PPT)
专题三 整式的乘法与因式分解
期末复习课
LOGO
掌握幂的相关运算法则,掌握整式的乘除运算法则.
1
掌握平方差公式和完全平方公式,并能利用公式进行乘法运算.
2
能用提公因式法、公式法进行因式分解.
3
复习目标
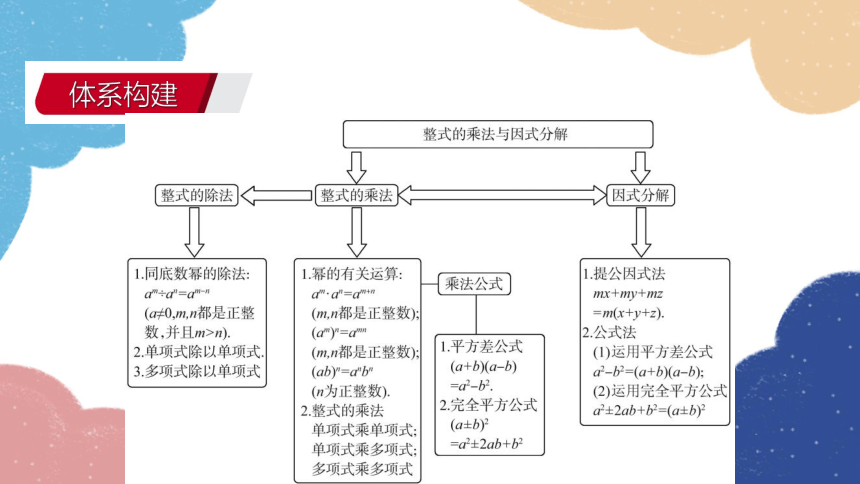
体系构建
考点一 幂的运算
考点精析
【归纳总结】幂的运算要注意什么?
考点精析
考点精析
【变式训练】
考点精析
【变式训练】
考点精析
考点二 整式的乘法
考点精析
考点二 整式的乘法
考点二 整式的乘法
考点精析
【归纳总结】多项式的乘除法运算要注意什么?
考点精析
考点精析
C
【变式训练】
考点精析
【变式训练】
考点精析
考点三 乘法公式
考点三 乘法公式
考点精析
【归纳总结】怎样利用乘法公式求解化简求值问题?
考点精析
考点精析
【变式训练】
考点精析
【变式训练】
考点精析
【变式训练】
考点四 因式分解
考点精析
D
【归纳总结】因式分解有哪些步骤?
考点精析
考点精析
【变式训练】
考点精析
【变式训练】
本节复习的知识 ;
运用的思想、方法是 ;
经历的学习过程是 ;
最大的收获是 ;
应注意的问题是 .
课堂小结
整式的乘法与因式分解
整式的除法
整式的乘法
因式分解
1.同底数幂的除法:
1幂的有关运算:
1.提公因式法
乘法公式
am÷a"=am-n
am·q"=am+n
mx+my+mz
(a≠0,m,n都是正整
(m,n都是正整数);
=1m(x+y+z).
数,并且m>n).
(a")y”=dn
2.公式法
2.单项式除以单项式
(,n都是正整数);
1.平方差公式
(1)运用平方差公式
3.多项式除以单项式
(ab)"=a"bm
(a+b)(a-b)
a2-b2=(a+b)(a-b):
(n为正整数).
=a2-b2.
(2)运用完全平方公式
2.整式的乘法
2.完全平方公式
a2±2ab+b2=(a±b)2
单项式乘单项式:
(a±b)2
单项式乘多项式;
=a2±2ab+b2
多项式乘多项式
专题三 整式的乘法与因式分解
期末复习课
LOGO
掌握幂的相关运算法则,掌握整式的乘除运算法则.
1
掌握平方差公式和完全平方公式,并能利用公式进行乘法运算.
2
能用提公因式法、公式法进行因式分解.
3
复习目标
体系构建
考点一 幂的运算
考点精析
【归纳总结】幂的运算要注意什么?
考点精析
考点精析
【变式训练】
考点精析
【变式训练】
考点精析
考点二 整式的乘法
考点精析
考点二 整式的乘法
考点二 整式的乘法
考点精析
【归纳总结】多项式的乘除法运算要注意什么?
考点精析
考点精析
C
【变式训练】
考点精析
【变式训练】
考点精析
考点三 乘法公式
考点三 乘法公式
考点精析
【归纳总结】怎样利用乘法公式求解化简求值问题?
考点精析
考点精析
【变式训练】
考点精析
【变式训练】
考点精析
【变式训练】
考点四 因式分解
考点精析
D
【归纳总结】因式分解有哪些步骤?
考点精析
考点精析
【变式训练】
考点精析
【变式训练】
本节复习的知识 ;
运用的思想、方法是 ;
经历的学习过程是 ;
最大的收获是 ;
应注意的问题是 .
课堂小结
整式的乘法与因式分解
整式的除法
整式的乘法
因式分解
1.同底数幂的除法:
1幂的有关运算:
1.提公因式法
乘法公式
am÷a"=am-n
am·q"=am+n
mx+my+mz
(a≠0,m,n都是正整
(m,n都是正整数);
=1m(x+y+z).
数,并且m>n).
(a")y”=dn
2.公式法
2.单项式除以单项式
(,n都是正整数);
1.平方差公式
(1)运用平方差公式
3.多项式除以单项式
(ab)"=a"bm
(a+b)(a-b)
a2-b2=(a+b)(a-b):
(n为正整数).
=a2-b2.
(2)运用完全平方公式
2.整式的乘法
2.完全平方公式
a2±2ab+b2=(a±b)2
单项式乘单项式:
(a±b)2
单项式乘多项式;
=a2±2ab+b2
多项式乘多项式
同课章节目录
