3.2平面直角坐标系(第3课时) 课件 (共26张PPT)2023—2024学年北师大版数学八年级上册
文档属性
| 名称 | 3.2平面直角坐标系(第3课时) 课件 (共26张PPT)2023—2024学年北师大版数学八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 343.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-21 13:13:32 | ||
图片预览




文档简介
(共26张PPT)
3.2平面直角坐标系
(第3课时)
---建立适当平面直角坐标系
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
原点
第一象限
第四象限
第三象限
第二象限
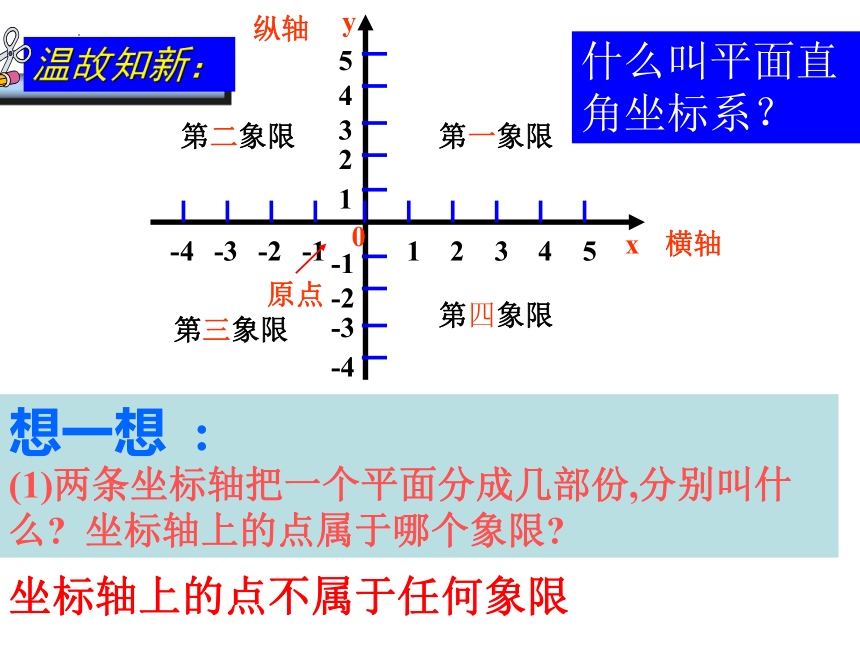
想一想 : (1)两条坐标轴把一个平面分成几部份,分别叫什么 坐标轴上的点属于哪个象限
什么叫平面直角坐标系?
坐标轴上的点不属于任何象限
温故知新:
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
原点
第一象限
第四象限
第三象限
第二象限
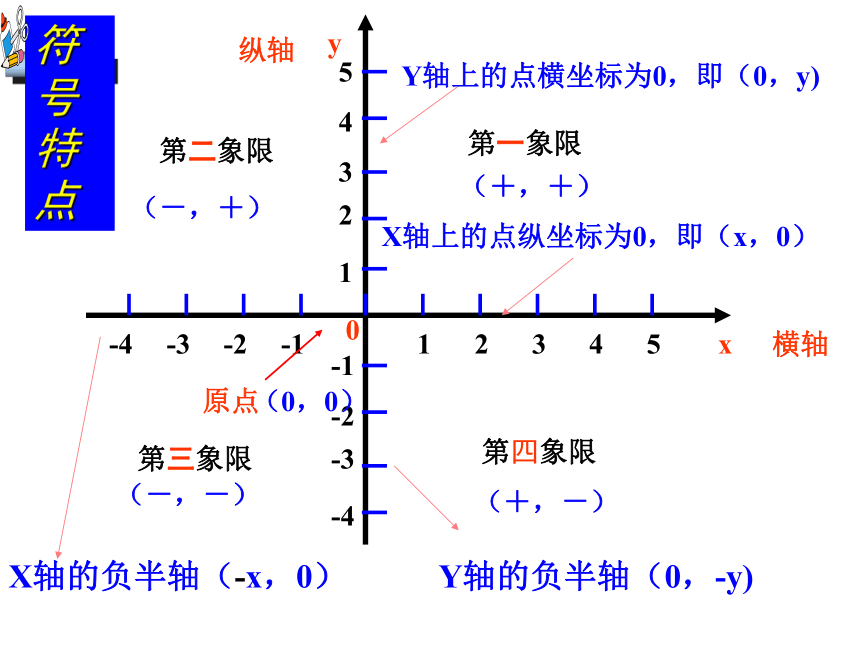
X轴上的点纵坐标为0,即(x,0)
Y轴上的点横坐标为0,即(0,y)
(+,+)
(-,+)
(-,-)
(+,-)
(0,0)
符号特点
Y轴的负半轴(0,-y)
X轴的负半轴(-x,0)
(1)点(-3,2)在第_____象限;
二
(2)点(1.5,-1)在第_______象限;
四
(3)点( -3 ,0)在____ 轴上;
x
(4)若点(-3, a + 5)在x轴上,则a=______.
- 5
(5)点 M( -3,-4)到 x轴的距离是_________,
到 y轴的距离是________,
到 原点的距离是________.
4
3
5
小练习
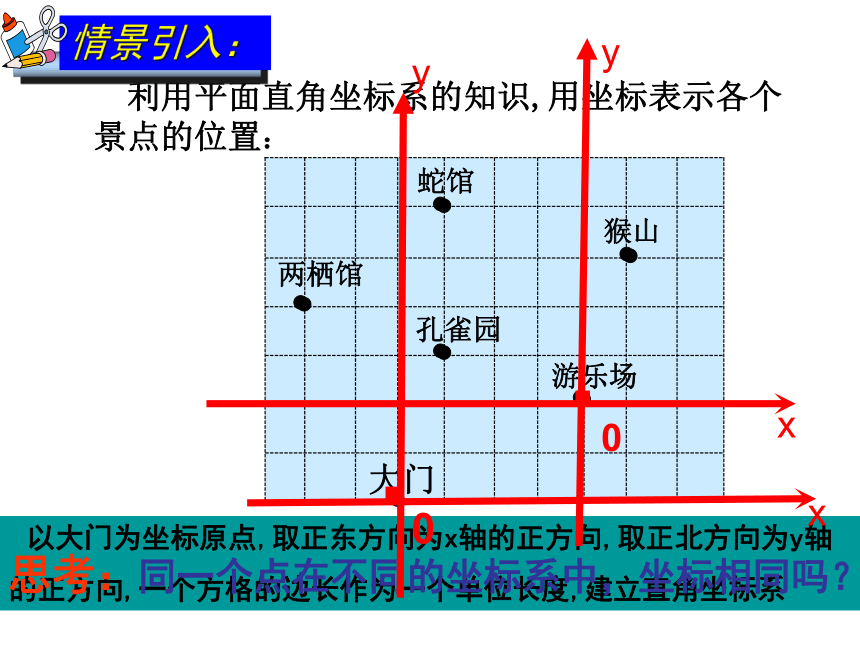
以大门为坐标原点,取正东方向为x轴的正方向,取正北方向为y轴
的正方向,一个方格的边长作为一个单位长度,建立直角坐标系
利用平面直角坐标系的知识,用坐标表示各个景点的位置:
大门
游乐场
猴山
蛇馆
两栖馆
孔雀园
思考:同一个点在不同的坐标系中,坐标相同吗?
情景引入:
.
0
.
y
x
y
x
0
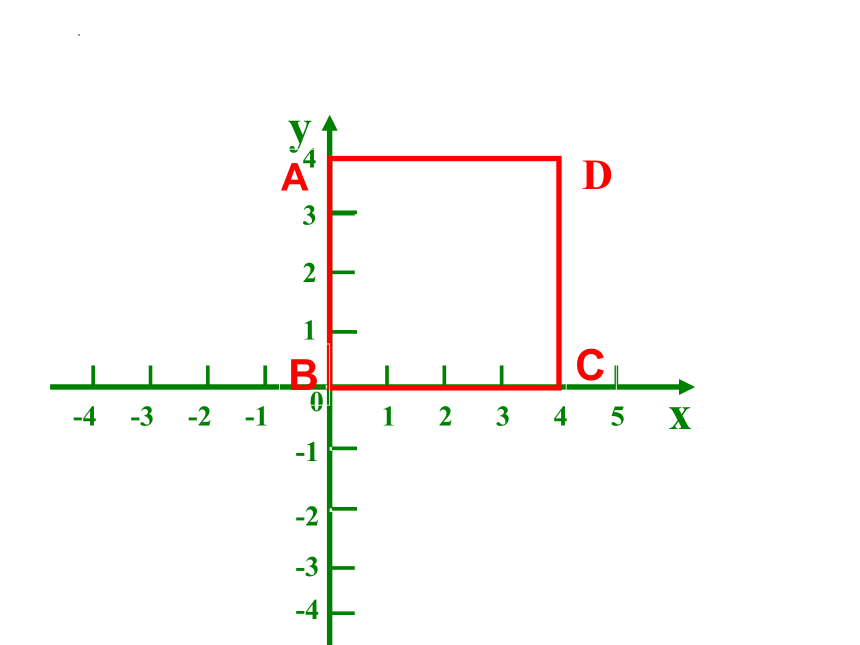
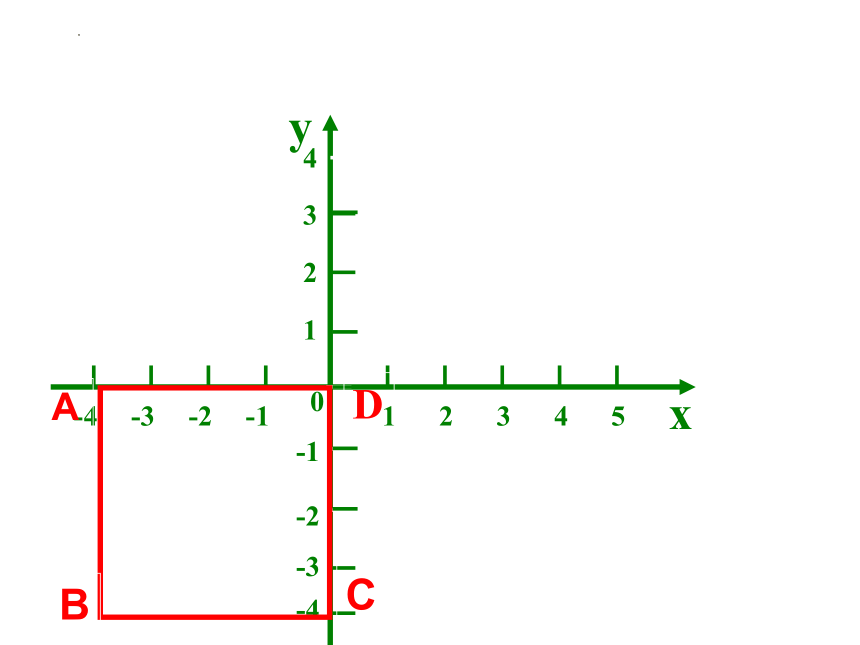
正方形边长为4,请你建立一个平面直角坐标系,并求出各点的坐标.
(1)你是如何建立的平面直角坐标系
(即:如何确定的原点和坐标轴)
(2)各点坐标如何求得
A
B
C
D
尝试练习1:
学习新课:
0
1
2
3
4
5
-4
-3
-2
-1
3
1
2
-2
-1
-3
4
-4
x
y
B
C
D
A
0
1
2
3
4
5
-4
-3
-2
-1
3
1
2
-2
-1
-3
4
-4
x
y
B
C
D
A
0
1
2
3
4
5
-4
-3
-2
-1
3
1
2
-2
-1
-3
4
-4
x
y
B
C
D
A
0
1
2
3
4
5
-4
-3
-2
-1
3
1
2
-2
-1
-3
4
-4
x
y
(1)以某已知点为原点,使它的坐标为(0,0);
(2)以图形中某线段所在的直线为x轴或y轴;
B
C
D
A
0
1
2
3
4
5
-4
-3
-2
-1
3
1
2
-2
-1
-3
4
-4
x
y
B
C
D
A
0
1
2
3
4
5
-4
-3
-2
-1
3
1
2
-2
-1
-3
4
-4
x
y
(3)利用图形的轴对称性,以对称轴为坐标轴;
B
C
D
A
建立平面直角坐标系的步骤
(1):选原点
(2):画坐标轴
(3):建立平面直角坐标系
小结
尝试练习2:
如图,矩形ABCD的长与宽分别是
6,4,建立适当的直角坐标系,
并写出各个顶点的坐标.
A
B
C
D
B
C
D
A
解: 以点C为原点, 分别以CD , CB所在的直线为x 轴, y 轴建立直角坐标系. 此时C点坐标为( 0 , 0 ).
x
y
0
(0 , 0 )
( 0 , 4 )
( 6 , 4 )
( 6 , 0)
由CD长为6,
CB长为4, 可得
D , B , A的坐标
分别为
D( 6 , 0 ),
B( 0 , 4 ),
A( 6 , 4 ) .
B
C
D
A
解: 以点C为原点, 分别以CD , CB所在的直线为x 轴, y 轴建立直角坐标系. 此时D点坐标为( 0 , 0 ).
x
y
0
(-6 , 0 )
( -6 , 4 )
(0 , 4)
( 0 , 0)
由CD长为6,
CB长为4, 可得
D , B , A的坐标
分别为
C( -6 , 0 ),
B( -6 , 4 ),
A( 0 , 4 ) .
B
C
D
A
解: 以点C为原点, 分别以BA , DA所在的直线为x 轴, y 轴建立直角坐标系. 此时A点坐标为( 0 , 0 ).
x
y
0
(-6 , -4 )
( -6 , 0)
( 0 , 0 )
( 0 , -4)
由CD长为6,
CB长为4, 可得
D , B , A的坐标
分别为
D( 0 , -4 ),
B( -6 , 0 ),
C( -6 , -4 ) .
解:
A
B
C
D
x
y
0
3
-3
2
-2
以长方形的中心为坐标原点,平行于BC、BA的直线为x轴、y轴,建立直角坐标系.坐标分别为A(-3,2),B(-3,-2),C(3,-2),
D(3,2)
1.矩形ABCD的长为4,宽为3,建立适当的直角坐标系,并写出各点的坐标.
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
A
B
C
D
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
还有其他方法吗
x
x
y
y
练习
尝试练习3
对于边长为4的正三角形△ABC,
建立适当的直角坐标系,
写出各个顶点的坐标.
A
B
C
对于边长为4的正三角形△ABC,
建立适当的直角坐标系,写出各个顶点的坐标.
A
B
C
思考:怎样求出A的纵坐标呢?
x
y
o
x
y
o
x
y
o
解:以BC中点为坐标原点,
以BC所在的直线为x轴,
以BC的中垂线为y轴,
建立直角坐标系.
在等边三角形ABC中,
由等边三角形性质可知:AB=4,BO=CO=2,
A
B
C
x
y
o
因此,顶点A,B,C的坐标分别为A(0, ),
B (-2,0),C(2,0).
在一次“寻宝”游戏中,寻宝人已经找到了坐标为(3, 2)和(3, 2)的两个标志点,并且知道藏宝
地点的坐标为(4, 4),除此之外不知道其他信息。
如何确定直角坐标系找到“宝藏”?
(3, 2)
(3, –2)
x
y
O
(4, 4)
“寻宝”游戏
1、如图,象棋盘中的小方格均为边长为1个单位
的正方形,“炮”的坐标为(–2, 1),“帅”的坐标为
(1, –1),则“卒”的坐标为 。
x
y
O
炮
帅
卒
巩固练习
巩固练习
2.如图,A、B两点的坐标分别为(2, 1),(2, 1),
你能确定(3, 3)的位置吗?
总结收获
通过本节课的学习,
你认为怎样建立恰当 的平面直角坐标系?
(1)以某已知点为原点,使它的坐标为(0,0);
(2)以图形中某线段所在直线为x轴或y轴;
(3)利用图形的以对称轴为x轴或y轴;
(4)以已知线段中点为原点.
3.2平面直角坐标系
(第3课时)
---建立适当平面直角坐标系
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
原点
第一象限
第四象限
第三象限
第二象限
想一想 : (1)两条坐标轴把一个平面分成几部份,分别叫什么 坐标轴上的点属于哪个象限
什么叫平面直角坐标系?
坐标轴上的点不属于任何象限
温故知新:
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
原点
第一象限
第四象限
第三象限
第二象限
X轴上的点纵坐标为0,即(x,0)
Y轴上的点横坐标为0,即(0,y)
(+,+)
(-,+)
(-,-)
(+,-)
(0,0)
符号特点
Y轴的负半轴(0,-y)
X轴的负半轴(-x,0)
(1)点(-3,2)在第_____象限;
二
(2)点(1.5,-1)在第_______象限;
四
(3)点( -3 ,0)在____ 轴上;
x
(4)若点(-3, a + 5)在x轴上,则a=______.
- 5
(5)点 M( -3,-4)到 x轴的距离是_________,
到 y轴的距离是________,
到 原点的距离是________.
4
3
5
小练习
以大门为坐标原点,取正东方向为x轴的正方向,取正北方向为y轴
的正方向,一个方格的边长作为一个单位长度,建立直角坐标系
利用平面直角坐标系的知识,用坐标表示各个景点的位置:
大门
游乐场
猴山
蛇馆
两栖馆
孔雀园
思考:同一个点在不同的坐标系中,坐标相同吗?
情景引入:
.
0
.
y
x
y
x
0
正方形边长为4,请你建立一个平面直角坐标系,并求出各点的坐标.
(1)你是如何建立的平面直角坐标系
(即:如何确定的原点和坐标轴)
(2)各点坐标如何求得
A
B
C
D
尝试练习1:
学习新课:
0
1
2
3
4
5
-4
-3
-2
-1
3
1
2
-2
-1
-3
4
-4
x
y
B
C
D
A
0
1
2
3
4
5
-4
-3
-2
-1
3
1
2
-2
-1
-3
4
-4
x
y
B
C
D
A
0
1
2
3
4
5
-4
-3
-2
-1
3
1
2
-2
-1
-3
4
-4
x
y
B
C
D
A
0
1
2
3
4
5
-4
-3
-2
-1
3
1
2
-2
-1
-3
4
-4
x
y
(1)以某已知点为原点,使它的坐标为(0,0);
(2)以图形中某线段所在的直线为x轴或y轴;
B
C
D
A
0
1
2
3
4
5
-4
-3
-2
-1
3
1
2
-2
-1
-3
4
-4
x
y
B
C
D
A
0
1
2
3
4
5
-4
-3
-2
-1
3
1
2
-2
-1
-3
4
-4
x
y
(3)利用图形的轴对称性,以对称轴为坐标轴;
B
C
D
A
建立平面直角坐标系的步骤
(1):选原点
(2):画坐标轴
(3):建立平面直角坐标系
小结
尝试练习2:
如图,矩形ABCD的长与宽分别是
6,4,建立适当的直角坐标系,
并写出各个顶点的坐标.
A
B
C
D
B
C
D
A
解: 以点C为原点, 分别以CD , CB所在的直线为x 轴, y 轴建立直角坐标系. 此时C点坐标为( 0 , 0 ).
x
y
0
(0 , 0 )
( 0 , 4 )
( 6 , 4 )
( 6 , 0)
由CD长为6,
CB长为4, 可得
D , B , A的坐标
分别为
D( 6 , 0 ),
B( 0 , 4 ),
A( 6 , 4 ) .
B
C
D
A
解: 以点C为原点, 分别以CD , CB所在的直线为x 轴, y 轴建立直角坐标系. 此时D点坐标为( 0 , 0 ).
x
y
0
(-6 , 0 )
( -6 , 4 )
(0 , 4)
( 0 , 0)
由CD长为6,
CB长为4, 可得
D , B , A的坐标
分别为
C( -6 , 0 ),
B( -6 , 4 ),
A( 0 , 4 ) .
B
C
D
A
解: 以点C为原点, 分别以BA , DA所在的直线为x 轴, y 轴建立直角坐标系. 此时A点坐标为( 0 , 0 ).
x
y
0
(-6 , -4 )
( -6 , 0)
( 0 , 0 )
( 0 , -4)
由CD长为6,
CB长为4, 可得
D , B , A的坐标
分别为
D( 0 , -4 ),
B( -6 , 0 ),
C( -6 , -4 ) .
解:
A
B
C
D
x
y
0
3
-3
2
-2
以长方形的中心为坐标原点,平行于BC、BA的直线为x轴、y轴,建立直角坐标系.坐标分别为A(-3,2),B(-3,-2),C(3,-2),
D(3,2)
1.矩形ABCD的长为4,宽为3,建立适当的直角坐标系,并写出各点的坐标.
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
A
B
C
D
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
还有其他方法吗
x
x
y
y
练习
尝试练习3
对于边长为4的正三角形△ABC,
建立适当的直角坐标系,
写出各个顶点的坐标.
A
B
C
对于边长为4的正三角形△ABC,
建立适当的直角坐标系,写出各个顶点的坐标.
A
B
C
思考:怎样求出A的纵坐标呢?
x
y
o
x
y
o
x
y
o
解:以BC中点为坐标原点,
以BC所在的直线为x轴,
以BC的中垂线为y轴,
建立直角坐标系.
在等边三角形ABC中,
由等边三角形性质可知:AB=4,BO=CO=2,
A
B
C
x
y
o
因此,顶点A,B,C的坐标分别为A(0, ),
B (-2,0),C(2,0).
在一次“寻宝”游戏中,寻宝人已经找到了坐标为(3, 2)和(3, 2)的两个标志点,并且知道藏宝
地点的坐标为(4, 4),除此之外不知道其他信息。
如何确定直角坐标系找到“宝藏”?
(3, 2)
(3, –2)
x
y
O
(4, 4)
“寻宝”游戏
1、如图,象棋盘中的小方格均为边长为1个单位
的正方形,“炮”的坐标为(–2, 1),“帅”的坐标为
(1, –1),则“卒”的坐标为 。
x
y
O
炮
帅
卒
巩固练习
巩固练习
2.如图,A、B两点的坐标分别为(2, 1),(2, 1),
你能确定(3, 3)的位置吗?
总结收获
通过本节课的学习,
你认为怎样建立恰当 的平面直角坐标系?
(1)以某已知点为原点,使它的坐标为(0,0);
(2)以图形中某线段所在直线为x轴或y轴;
(3)利用图形的以对称轴为x轴或y轴;
(4)以已知线段中点为原点.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
