八年级数学上分层优化堂堂清(2)12.2全等三角形的判定第一课时(含解析)
文档属性
| 名称 | 八年级数学上分层优化堂堂清(2)12.2全等三角形的判定第一课时(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-20 15:51:55 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
八年级数学上分层优化堂堂清
十二章 三角形
12.2三角形全等的判定第一课时
学习目标:
经历实验探究的过程,直观发现三边相等的两个三角形全等。会用直规作图法作“一条线段等于已知线段,一个角等于已知角”,提高动手操作能力。知道这样作图的理由。
能利用“SSS”进行有关的计算或证明。发展逻辑推理能力、计算能力和空间观念。
老师对你说:
知识点1 全等三角形的判定1:边边边(SSS)
文字:在两个三角形中,如果有三条边对应相等,那么这两个三角形全等.
图形:
符号:在与中,
证明的书写步骤:
①准备条件:证全等时要用的条件要先证好;②指明范围:写出在哪两个三角形中;
③摆齐根据:摆出三个条件用大括号括起来;④写出结论:写出全等结论.
注意:(1)说明两三角形全等所需的条件应按对应边的顺序书写.
(2)结论中所出现的边必须在所证明的两个三角形中.
知识点2 用尺规作一个角等于已知角
已知:∠AOB.求作: ∠A′O′B′=∠AOB.
作法:(1)以点O 为圆心,任意长为半径画弧,分别交OA,OB 于点C、D;
(2)画一条射线O′A′,以点O′为圆心,OC 长为半径画弧,交O′A′于点C′;
(3)以点C′为圆心,CD 长为半径画弧,与第2 步中所画的弧交于点D′;
(4)过点D′画射线O′B′,则∠A′O′B′=∠AOB.
知识点3 运用边边边定理证明和计算
运用“SSS”证明两个三角形全等主要是找边相等,边相等除了题目中已知的边相等外,还有一些相等边隐含在题设或图形中。
基础提升 教材核心知识点精练
知识点1 全等三角形的判定1:边边边(SSS)
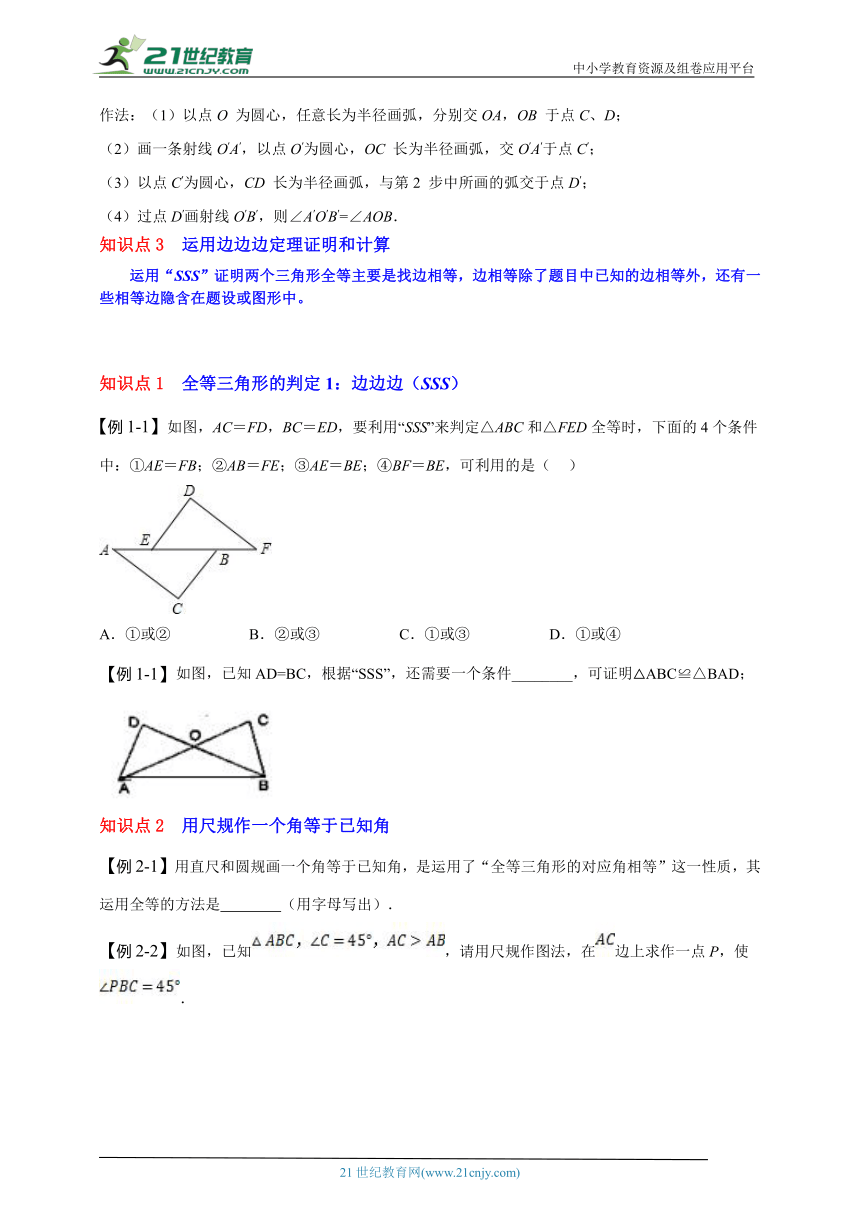
【例1-1】如图,AC=FD,BC=ED,要利用“SSS”来判定△ABC和△FED全等时,下面的4个条件中:①AE=FB;②AB=FE;③AE=BE;④BF=BE,可利用的是( )
A.①或② B.②或③ C.①或③ D.①或④
【例1-1】如图,已知AD=BC,根据“SSS”,还需要一个条件________,可证明△ABC≌△BAD;
知识点2 用尺规作一个角等于已知角
【例2-1】用直尺和圆规画一个角等于已知角,是运用了“全等三角形的对应角相等”这一性质,其运用全等的方法是 (用字母写出).
【例2-2】如图,已知,请用尺规作图法,在边上求作一点P,使.
【例2-3】已知,为射线上一点,在内部,求作,使.(保留作图痕迹,不写作法)
知识点3 运用边边边定理证明和计算
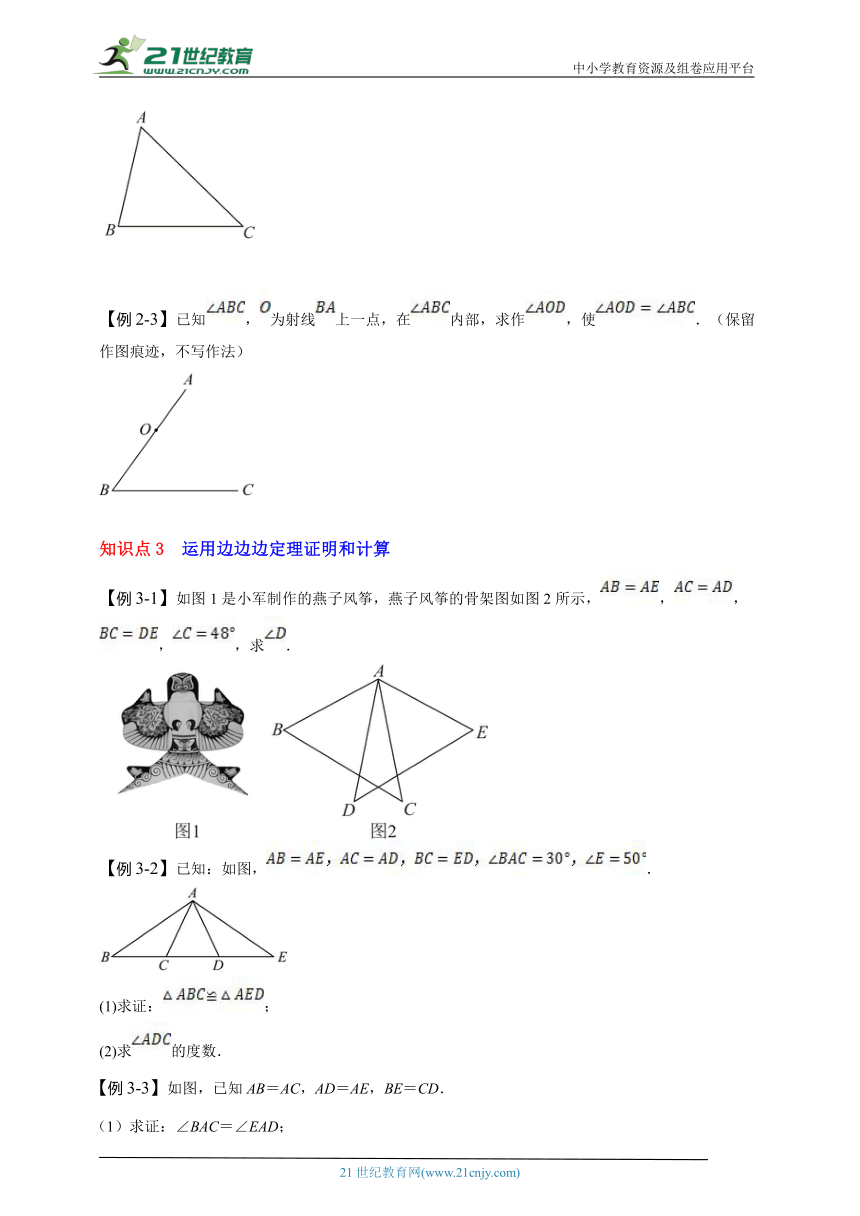
【例3-1】如图1是小军制作的燕子风筝,燕子风筝的骨架图如图2所示,,,,,求.
【例3-2】已知:如图,.
(1)求证:;
(2)求的度数.
【例3-3】如图,已知AB=AC,AD=AE,BE=CD.
(1)求证:∠BAC=∠EAD;
(2)写出∠1,∠2,∠3之间的数量关系,并予以证明.
能力强化提升训练
1 .如图,已知,,,直线与,分别交于点,,且,,则的度数为___________.
2 .莆仙戏是现存最古老的地方戏剧种之一,被称为“宋元南戏的活化石”,2021年5月莆仙戏《踏伞行》获评为“2020年度国家舞台艺术精品创作扶持工程重点扶持剧目”.该剧中“油纸伞”无疑是最重要的道具,依伞设戏,情节新颖,结构巧妙,谱写了一曲美轮美奂、诗意盎然的传统戏曲乐歌.“油纸伞”的制作工艺十分巧妙.如图,伞圈D沿着伞柄滑动时,总有伞骨,,从而使得伞柄AP始终平分同一平面内两条伞骨所成的.为什么?
3.如图,已知,,求证.
4 .已知:如图1,在中,.求作:射线,使得.
下面是小明设计的尺规作图过程.
作法:如图2,
①以点为圆心,适当长为半径作弧,分别交,于,两点;
②以点为圆心,长为半径作弧,交的延长线于点;
③以点为圆心,长为半径作弧,两弧在内部交于点;
④作射线.所以射线就是所求作的射线.
根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:连接,.
,,.
__________,
__________,
(__________)(填推理的依据).
堂堂清
选择题(每小题4分,共32分)
1 .如图,在中,,D为中点,,则的度数是( )
A. B. C. D.
2 .工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M、N重合,过角尺顶点C作射线OC,由此作法便可得△NOC≌△MOC,其依据是( )
A.SSS B.SAS C.ASA D.AAS
3.如图,点C在的边OB上,尺规作图痕迹显示的是( )
A.作线段CE的垂直平分线 B.作的平分线
C.连接EN,则是等边三角形 D.作
4 .如图,,,则,其依据是( )
A. B. C. D.
5 .如图,已知,,是上两点且,若,,则的度数为( )
A. B. C. D.
6 .如图,AC=FD,BC=ED,要利用“SSS”来判定△ABC和△FED全等时,下面的4个条件中:①AE=FB;②AB=FE;③AE=BE;④BF=BE,可利用的是( )
A.①或② B.②或③ C.①或③ D.①或④
7 .如图,在△ABC和△DEB中,点C在BD边上,AC与BE交于F,若AB=DE,BC=EB,AC=DB,则∠ACB等于( )
A.∠D B.∠E C.2∠ABF D.∠AFB
8 .如图,点E、D分别在AB、AC上,若AB=AC,BE=CD,BD=EC,,,则∠BOC度数是( )
A. B. C. D.
二、填空题(每小题4分,共20分)
9 .如图,在和中,,,,则________ .
如图,若、,,,则_________.
11 .如图,用直尺和圆规作一个角等于已知角的过程中,依据全等三角形的性质可得,这里判断的依据是___________.
12 .2022年10月12日某中学八年级(4)班的同学在听了“天宫课堂”第三课,即我国航天员在中国空间站进行的太空授课后,组成数学兴趣小组进行了设计伞的实践活动.康康所在的小组依据全等三角形的判定设计了截面如图所示的伞骨结构,当伞完全打开后,测得,E,F分别是,的中点,,那么的依据是________
13 .如图,与交于点,①;②;③,请以①②③中的两个作为条件,另一个为结论,写出一个正确命题.
正确的命题是:____________________(格式:由××,得×;上述×用前面数字代号①②③表示).
三、解答题(共6小题,48分)
14 .(8分)已知:如图,点A,C,B,D都在一条直线上,AC=BD,AM=CN,BM=DN.求证:AM∥CN.
15 .(8分)如图,是的中点,.求证:.
16 .(8分)如图,在四边形ABCD中,,.求证:.
17 .(8分)如图,为线段外一点.
(1)求作直线,使得;(要求:尺规作图,不写作法,保留作图痕迹)
(2)根据作图,说明你画的直线符合要求的原因.
18 .如图,在四边形中,与相交于点E.
求证:.
19 .(8分)如图,已知,.求证:.
拓展培优*冲刺满分
1.已知,如图,,求证:
2.尺规作图之旅
下面是一副纯手绘的画作,其中用到的主要工具就是直尺和圆规,在数学中,我们也能通过尺规作图创造出许多带有美感的图形.
尺规作图起源于古希腊的数学课题,只允许使用圆规和直尺,来解决平面几何作图问题.
【作图原理】在两年的数学学习里中,我们认识了尺规作图,并学会用尺规作图完成一些作图问题,请仔细思考回顾,判断以下操作能否通过尺规作图实现,可以实现的画√,不能实现的 画×.
(1)过一点作一条直线.( )
(2)过两点作一条直线.( )
(3)画一条长为3㎝的线段.( )
(4)以一点为圆心,给定线段长为半径作圆.( )
【回顾思考】还记得我们用尺规作图完成的第一个问题吗?那就是“作一条线段等于已知线段”,接着,我们学习了使用尺规作图作线段的垂直平分线,作角平分线,过直线外一点作垂线……而这些尺规作图的背后都与我们学习的数学原理密切相关,下面是用尺规作一个角等于已知角的方法及说理,请补全过程.
已知:∠AOB.
求作:使
作法:(1)如图,以O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;
(2)画一条射线,以点为圆心,OC长为半径画弧,交于点;
(3)以点为圆心,____________________;
(4)过点画射线,则.
说理:由作法得已知:
求证:
证明:
( )
所以( )
【小试牛刀】请按照上面的范例,完成尺规作图并说理:过直线外一点作已知直线的平行线.
已知:直线与直线外一点A.
求作:过点A的直线,使得.
【创新应用】现实生活中许多图案设计都蕴含着数学原理,下面是一个常见商标的设计示意图.假设你拥有一家书店,请利用你手中的刻度尺和圆规,为你的书店设计一个图案.要求保留作图痕迹,并写出你的设计意图.
八年级数学上分层优化堂堂清
十二章 全等三角形
12.2三角形全等的判定第一课时(解析版)
学习目标:
经历实验探究的过程,直观发现三边相等的两个三角形全等。会用直规作图法作“一条线段等于已知线段,一个角等于已知角”,提高动手操作能力。知道这样作图的理由。
能利用“SSS”进行有关的计算或证明。发展逻辑推理能力、计算能力和空间观念。
老师对你说:
知识点1 全等三角形的判定1:边边边(SSS)
文字:在两个三角形中,如果有三条边对应相等,那么这两个三角形全等.
图形:
符号:在与中,
证明的书写步骤:
①准备条件:证全等时要用的条件要先证好;②指明范围:写出在哪两个三角形中;
③摆齐根据:摆出三个条件用大括号括起来;④写出结论:写出全等结论.
注意:(1)说明两三角形全等所需的条件应按对应边的顺序书写.
(2)结论中所出现的边必须在所证明的两个三角形中.
知识点2 用尺规作一个角等于已知角
已知:∠AOB.求作: ∠A′O′B′=∠AOB.
作法:(1)以点O 为圆心,任意长为半径画弧,分别交OA,OB 于点C、D;
(2)画一条射线O′A′,以点O′为圆心,OC 长为半径画弧,交O′A′于点C′;
(3)以点C′为圆心,CD 长为半径画弧,与第2 步中所画的弧交于点D′;
(4)过点D′画射线O′B′,则∠A′O′B′=∠AOB.
知识点3 运用边边边定理证明和计算
运用“SSS”证明两个三角形全等主要是找边相等,边相等除了题目中已知的边相等外,还有一些相等边隐含在题设或图形中。
基础提升 教材核心知识点精练
知识点1 全等三角形的判定1:边边边(SSS)
【例1-1】如图,AC=FD,BC=ED,要利用“SSS”来判定△ABC和△FED全等时,下面的4个条件中:①AE=FB;②AB=FE;③AE=BE;④BF=BE,可利用的是( )
A.①或② B.②或③ C.①或③ D.①或④
【答案】A
【分析】根据全等三角形的SSS判定条件解答即可.
【详解】解:∵AE=FB,
∴AE+BE=FB+BE,
∴AB=FE,
在△ABC和△FED中,
,
∴△ABC≌△FED(SSS),
∵AE=BE和BF=BE推不出AB=FE,
∴可利用的是①或②,
故选:A.
【点评】本题考查全等三角形的判定,熟练掌握全等三角形的判定方法是解答的关键.
【例1-1】如图,已知AD=BC,根据“SSS”,还需要一个条件________,可证明△ABC≌△BAD;
【答案】DB=CA
【解析】图形中隐含条件AB=BA,找出第三边BD和AC即可;
在△ABC和△BAD中 ,∴△ABC≌△BAD(SSS)
【点评】本题考查全等三角形的判定,熟练掌握全等三角形的判定方法是解答的关键.
知识点2 用尺规作一个角等于已知角
【例2-1】用直尺和圆规画一个角等于已知角,是运用了“全等三角形的对应角相等”这一性质,其运用全等的方法是 (用字母写出).
【分析】根据用直尺和圆规画一个角等于已知角的过程很容易看出所得两个三角形三边对应相等.
【解答】
解:①设已知角的顶点为O,以O为圆心,任意长度为半径画圆,交角两边为A,B两点;
②用直尺画一条射线,端点为M,以M为圆心,用同样的半径画圆,该圆为圆M,交射线为C点;
③以A为圆心,以AB为半径画圆,然后以C点为圆心,以同样的半径画圆,交圆M于D,E两点,随意连MD或者ME;得到的∠CMD就是所求的角;由以上作角过程不难看出有三个对应边相等.
∴证明全等的方法是SSS.故答案为:SSS.
【点评】本题考查的关键是作角的过程,作角过程中所产生的条件就是证明全等的条件.
【例2-2】如图,已知,请用尺规作图法,在边上求作一点P,使.
【答案】见解析
【详解】根据作与已知角相等的角的尺规作图方法作图即可.
【分析】解:如图所示,点P即为所求.
【点评】本题主要考查了尺规作图—作与已知角相等的角,熟知相关作图方法是解题的关键.
【例2-3】已知,为射线上一点,在内部,求作,使.(保留作图痕迹,不写作法)
【答案】图见解析
【分析】根据作角等于已知角的方法,进行作图即可.
【详解】解:如图所示,即为所求;
【点评】本题考查作角等于已知角.熟练掌握尺规作图方法,是解题的关键.
知识点3 运用边边边定理证明和计算
【例3-1】如图1是小军制作的燕子风筝,燕子风筝的骨架图如图2所示,,,,,求.
【答案】
【分析】根据题意,直接根据证明,再根据全等三角形对应角相等,即可求解.
【详解】解:在和中,
,
∴,
∴.
【点评】本题主要考查了三角形全等的判定和性质,解题的关键是掌握全等三角形的判定方法以及全等三角形对应边相等,对应角相等.判定三角形全等的方法是.
【例3-2】已知:如图,.
(1)求证:;
(2)求的度数.
【答案】(1)证明见解析
(2)
【分析】(1)直接利用证明即可;
(2)先根据全等三角形的性质得到,再利用三角形外角的性质求解即可.
【详解】(1)证明:在和中,
,
∴;
(2)解:∵,
∴,
∴.
【点评】本题主要考查了全等三角形的性质与判定,三角形外角的性质,熟知全等三角形的性质与判定条件是解题的关键.
【例3-3】如图,已知AB=AC,AD=AE,BE=CD.
(1)求证:∠BAC=∠EAD;
(2)写出∠1,∠2,∠3之间的数量关系,并予以证明.
【答案】(1)见解析;(2)∠3=∠1+∠2,见解析
【分析】(1)根据SSS证△BAE≌△CAD,推出∠BAE=∠CAD即可;
(2)根据全等三角形性质推出∠1=∠BAE,∠2=∠ABE,代入∠3=∠BAE+∠ABE求出即可.
【详解】(1)证明:在△ABE和△ACD中,
∵AB=AC,AD=AE,BE=CD
∴△ABE≌△ACD(SSS),
∴∠BAE=∠CAD.
∴∠BAE+ EAC=∠CAD+ EAC .
∴∠BAC=∠EAD.
(2) ∠3=∠1+∠2;
理由如下:由图中知,
∠3=∠ABE+∠BAE
又由(1)中知△ABE≌△ACD,
∴ ∠ABE=∠2 , ∠BAE=∠1
∴ ∠3=∠1+∠2
【点评】本题考查了全等三角形的性质和判定,三角形外角的性质,注意:全等三角形的对应角相等.
能力强化提升训练
1 .如图,已知,,,直线与,分别交于点,,且,,则的度数为___________.
【答案】
【分析】根据SSS得到,进而得到,,再结合对顶角相等,可得,最后再利用角的和差即可求解.
【详解】解:∵,,,
,
,,
与是对顶角,
∴,
∴,
∴,
∴,
故答案为:10°.
【点评】本题考查全等三角形的判定与性质,对顶角的性质、角的和差计算等内容,识别出与这一组对顶角,得到的度数是解题的关键.
2 .莆仙戏是现存最古老的地方戏剧种之一,被称为“宋元南戏的活化石”,2021年5月莆仙戏《踏伞行》获评为“2020年度国家舞台艺术精品创作扶持工程重点扶持剧目”.该剧中“油纸伞”无疑是最重要的道具,依伞设戏,情节新颖,结构巧妙,谱写了一曲美轮美奂、诗意盎然的传统戏曲乐歌.“油纸伞”的制作工艺十分巧妙.如图,伞圈D沿着伞柄滑动时,总有伞骨,,从而使得伞柄AP始终平分同一平面内两条伞骨所成的.为什么?
【答案】见解析
【分析】利用SSS证明,即可得到,由此证得结论.
【详解】证明:∵在和中,
,∴,∴,即AP平分.
【点评】此题考查了全等三角形的判定及性质,熟记全等三角形的判定定理是解题的关键.
如图,已知,,求证.
【答案】见解析
【分析】利用证明,根据全等三角形的性质可得,,再由,,即可得出
【详解】解:在和中,
,
∴,
∴,,
又∵,,
∴
【点评】本题主要考查全等三角形的判定和性质,熟练掌握全等三角形的判定和性质是解题的关键.
4 .已知:如图1,在中,.求作:射线,使得.
下面是小明设计的尺规作图过程.
作法:如图2,
①以点为圆心,适当长为半径作弧,分别交,于,两点;
②以点为圆心,长为半径作弧,交的延长线于点;
③以点为圆心,长为半径作弧,两弧在内部交于点;
④作射线.所以射线就是所求作的射线.
根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:连接,.
,,.
__________,
__________,
(__________)(填推理的依据).
【答案】(1)见解析;(2),,同位角相等两直线平行
【分析】(1)根据要求作出图形即可.
(2)利用全等三角形的性质证明即可.
【详解】解:(1)如图,射线即为所求作.
(2)连接,.
,,.
,
,
(同位角相等两直线平行).
故答案为:,,同位角相等两直线平行.
【点评】本题考查作图-复杂作图,全等三角形的判定和性质,平行线的判定等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
堂堂清
选择题(每小题4分,共32分)
1 .如图,在中,,D为中点,,则的度数是( )
A. B. C. D.
【答案】A
【分析】证明得到,,即可利用三角形内角和定理求出答案.
【详解】解:∵D为中点,
∴,
又∵,
∴,
∴,,
又∵,
∴,
∴,
故选A.
【点评】本题主要考查了全等三角形的性质与判定,三角形内角和定理,证明是解题的关键.
2 .工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M、N重合,过角尺顶点C作射线OC,由此作法便可得△NOC≌△MOC,其依据是( )
A.SSS B.SAS C.ASA D.AAS
答案 A
解析 ∵在△ONC和△OMC中,∴△MOC≌△NOC(SSS),
∴∠BOC=∠AOC,故选:A.
3.如图,点C在的边OB上,尺规作图痕迹显示的是( )
A.作线段CE的垂直平分线 B.作的平分线
C.连接EN,则是等边三角形 D.作
【答案】D
【分析】根据作图得出△ODM≌△CEN(SSS),得出∠MAD=∠NCE,得出OM∥CN即可.
【详解】解:连结EN ,
在△ODM和△CEN中,
,
∴△ODM≌△CEN(SSS),
∴∠MAD=∠NCE,
∴OM∥CN,
故选D.
【点评】本题考查尺规作图,掌握基本作图,三角形全等判定与性质,平行线的判定是解题关键.
4 .如图,,,则,其依据是( )
A. B. C. D.
【答案】C
【分析】由题可得,两个三角形三条对应边相等,则判断其全等依据为边边边.
解:在和中,
所以
故选:C
【点拨】本题考查三角形全等的判定,找到对应条件是解题的关键.
5 .如图,已知,,是上两点且,若,,则的度数为( )
A. B. C. D.
【答案】D
【分析】先证,得,再证,得,然后由三角形的外角性质即可得出结论.
【详解】解:在和中,
,
∴,
∴,
在和中,
,
∴,
∴,
∵,
∴.
故选:D.
【点评】本题主要考查了全等三角形的判定与性质以及三角形的外角性质等知识,熟练掌握全等三角形的判定与性质是解题的关键.
6 .如图,AC=FD,BC=ED,要利用“SSS”来判定△ABC和△FED全等时,下面的4个条件中:①AE=FB;②AB=FE;③AE=BE;④BF=BE,可利用的是( )
A.①或② B.②或③ C.①或③ D.①或④
【答案】A
【分析】根据全等三角形的SSS判定条件解答即可.
解:∵AE=FB,
∴AE+BE=FB+BE,
∴AB=FE,
在△ABC和△FED中,
,
∴△ABC≌△FED(SSS),
∵AE=BE和BF=BE推不出AB=FE,
∴可利用的是①或②,
故选:A.
【点拨】本题考查全等三角形的判定,熟练掌握全等三角形的判定方法是解答的关键.
7 .如图,在△ABC和△DEB中,点C在BD边上,AC与BE交于F,若AB=DE,BC=EB,AC=DB,则∠ACB等于( )
A.∠D B.∠E C.2∠ABF D.∠AFB
D
【分析】先根据SSS定理得出△ABC≌△DEB(SSS),故∠ACB=∠EBD,再根据∠AFB是△BFC的外角,可知∠AFB=∠ACB+∠EBD,由此可得出∠AFB=2∠ACB,故可得出结论.
解:在△ABC与△DEB中, ,
∴△ABC≌△DEB(SSS),
∴∠ACB=∠EBD.
∵∠AFB是△BFC的外角,
∴∠AFB=∠ACB+∠EBD,
∴∠AFB=2∠ACB,即∠AFB=∠ACB,
故选:D.
【点拨】本题考查的是全等三角形的判定与性质,熟知全等三角形的判定定理是解答此题的关键.
8 .如图,点E、D分别在AB、AC上,若AB=AC,BE=CD,BD=EC,,,则∠BOC度数是( )
A. B. C. D.
【答案】D
【分析】先利用SSS证明,利用全等三角形的性质推出,连接AO,延长至F,利用三角形外角的性质可得,由此可解.
解:∵AB=AC,BD=EC,
∴,即,
在和中,
,
∴,
∴,
如图,连接AO,延长AO至F,
根据三角形外角的性质可得,,,
∴,
故选:D.
【点拨】本题考查全等三角形的判定与性质,以及三角形外角的性质,证明是解题的关键.
二、填空题(每小题4分,共20分)
9 .如图,在和中,,,,则________ .
130
【分析】证明△ABC≌△ADC即可.
解:∵,,AC=AC,
∴△ABC≌△ADC,
∴∠D=∠B=130°,
故答案为:130.
【点拨】本题考查了全等三角形的判定和性质,掌握判定定理是解题关键.
如图,若、,,,则_________.
【分析】连接并延长至点E,先证明,得到,,再利用三角形外角的性质,求得,即可求出的度数.
解:如图,连接并延长至点E,
在和中,
,
,
,,
,,
故答案为:.
【点拨】本题考查了全等三角形的判定和性质,三角形外角的性质,作辅助线构造全等三角形是解题关键.
11 .如图,用直尺和圆规作一个角等于已知角的过程中,依据全等三角形的性质可得,这里判断的依据是___________.
【答案】
【分析】首先要清楚画图的步骤,步骤是以O为圆心,任意长为半径用圆规画弧,分别交于点;任意画一点,画射线,以为圆心,长为半径画弧交于点,以为圆心,长为半径画弧,可确定点的位置,过点画射线,就是与相等的角;则通过作图我们可以得到,接下来结合全等三角形的判定,即可解答.
解:根据作法可知,
∴,
故答案为:.
【点拨】本题考查尺规作图,解答本题的关键是掌握用尺规作一个角等于已知角的步骤,也考查了全等三角形的判定.
12 .2022年10月12日某中学八年级(4)班的同学在听了“天宫课堂”第三课,即我国航天员在中国空间站进行的太空授课后,组成数学兴趣小组进行了设计伞的实践活动.康康所在的小组依据全等三角形的判定设计了截面如图所示的伞骨结构,当伞完全打开后,测得,E,F分别是,的中点,,那么的依据是________
【答案】SSS
【分析】由E,F分别是,的中点,,得出;根据三边对应相等,证明.
解:∵E,F分别是,的中点,
∴
在与中
∴
故填SSS
【点拨】本题考查全等三角形的判定,解题的关键是熟练掌握全等三角形的判定定理.
13 .如图,与交于点,①;②;③,请以①②③中的两个作为条件,另一个为结论,写出一个正确命题.
正确的命题是:____________________(格式:由××,得×;上述×用前面数字代号①②③表示).
【答案】(1)由①③,得②;或由②③,得①;
【分析】分两种情形,利用全等三角形的判定和性质分别证明即可.
解:正确的命题是:由①③,得②;或由②③,得①;
证明:由①③,得②,
若,,
连接,
在和中,
,
,
;
或由②③,得①,
若,,
在和中,
,
,
,,
.
【点拨】本题考查命题,全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题.
三、解答题(共6小题,48分)
14 .(8分)已知:如图,点A,C,B,D都在一条直线上,AC=BD,AM=CN,BM=DN.求证:AM∥CN.
【答案】证明见详解.
【分析】首先根据可得,再加上条件 可利用SSS定理证明≌即可.
【详解】证明:
即
在和中,
∴≌(SSS),
∴∠A=∠NCD,
∴AM∥CN.
【点评】本题考查三角形全等判定,掌握三角形全等判定定理与方法是解题关键
15 .(8分)如图,是的中点,.求证:.
见分析
【分析】根据是的中点,得到,再利用证明两个三角形全等.
解:证明:是的中点,
,
在和中,
,
【点拨】本题考查了线段中点,三角形全等的判定,其中对三角形判定条件的确定是解决本题的关键.
16 .(8分)如图,在四边形ABCD中,,.求证:.
【答案】证明见解析
【分析】连接 证明再利用全等三角形的性质可得结论.
【详解】解:连接
四边形ABCD中,,,
【点评】本题考查的是全等三角形的判定与性质,构建全等三角形,利用证明三角形全等是解题的关键.
17 .(8分)如图,为线段外一点.
(1)求作直线,使得;(要求:尺规作图,不写作法,保留作图痕迹)
(2)根据作图,说明你画的直线符合要求的原因.
【答案】(1)见解析;(2)见解析
【分析】(1)先过点B作射线BE,且BE过点C,然后作,则直线即为所求的平行线;
(2)利用同位角相等,两直线平行即可判断.
【详解】解:(1)先过点B作射线BE,且BE过点C,然后作,
如图,直线即为所求的平行线;
(2)由作图可知,,
所以,
所以所画直线符合要求.
【点评】本题主要考查了尺规作图——作一个角等于已知角,平行线的判定,熟练掌握平行线的同位角相等,两直线平行是解题的关键.
18 .如图,在四边形中,与相交于点E.
求证:.
见分析
【分析】直接利用SSS证明△ACD≌△BDC,即可证明.
解:在△ACD和△BDC中,
,
∴△ACD≌△BDC(SSS),
∴∠DAC=∠CBD.
【点拨】本题考查了全等三角形的判定和性质,解题的关键是根据题意灵活运用SSS的方法.
19 .(8分)如图,已知,.求证:.
见详解.
【分析】根据SSS定理推出△ADB≌△BCA即可证明.
解:证明:在△ADB和△BCA中,
∴△ADB≌△BCA(SSS),
∴.
【点拨】本题考查了全等三角形的性质和判定,能正确进行推理证明全等是解此题的关键.
拓展培优*冲刺满分
1.已知,如图,,求证:
【答案】见详解
【分析】连接,证明即可求得答案.
【详解】证明:连接,如图所示,
∵,,,
∴,
∴;
【点评】本题考查了几何问题,正确作出辅助线是解题关键.
2.尺规作图之旅
下面是一副纯手绘的画作,其中用到的主要工具就是直尺和圆规,在数学中,我们也能通过尺规作图创造出许多带有美感的图形.
尺规作图起源于古希腊的数学课题,只允许使用圆规和直尺,来解决平面几何作图问题.
【作图原理】在两年的数学学习里中,我们认识了尺规作图,并学会用尺规作图完成一些作图问题,请仔细思考回顾,判断以下操作能否通过尺规作图实现,可以实现的画√,不能实现的 画×.
(1)过一点作一条直线.( )
(2)过两点作一条直线.( )
(3)画一条长为3㎝的线段.( )
(4)以一点为圆心,给定线段长为半径作圆.( )
【回顾思考】还记得我们用尺规作图完成的第一个问题吗?那就是“作一条线段等于已知线段”,接着,我们学习了使用尺规作图作线段的垂直平分线,作角平分线,过直线外一点作垂线……而这些尺规作图的背后都与我们学习的数学原理密切相关,下面是用尺规作一个角等于已知角的方法及说理,请补全过程.
已知:∠AOB.
求作:使
作法:(1)如图,以O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;
(2)画一条射线,以点为圆心,OC长为半径画弧,交于点;
(3)以点为圆心,____________________;
(4)过点画射线,则.
说理:由作法得已知:
求证:
证明:
( )
所以( )
【小试牛刀】请按照上面的范例,完成尺规作图并说理:过直线外一点作已知直线的平行线.
已知:直线与直线外一点A.
求作:过点A的直线,使得.
【创新应用】现实生活中许多图案设计都蕴含着数学原理,下面是一个常见商标的设计示意图.假设你拥有一家书店,请利用你手中的刻度尺和圆规,为你的书店设计一个图案.要求保留作图痕迹,并写出你的设计意图.
【答案】【作图原理】(1)√;(2)√;(3)×;(4)√;【回顾思考】作法:以点为圆心,以CD为半径画弧,与第二步中所画的弧相交于;说理:SSS,全等三角形对应角相等;【小试牛刀】答案见解析;【创新应用】答案见解析.
【分析】[作图原理]根据五种基本作图判断即可;
[回顾思考]利用全等三角形的判定解决问题即可;
[小试牛刀]利用同位角相等两直线平行解决问题即可;
[创新应用]答案不唯一,画出图形,说明设计意图即可.
【详解】解:[作图原理]:(1)过一点作一条直线.可以求作;
(2)过两点作一条直线.可以求作;
(3)画一条长为3cm的线段.不可以求作;
(4)以一点为圆心,给定线段长为半径作圆.可以求作;
故答案为:√,√,×,√;
[回顾思考]:作法:(1)如图,以O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;
(2)画一条射线OA,以点O为圆心,OC长为半径画弧,交OA于点C;
(3)以点C为圆心,以C′为圆心,CD长为半径画弧与第二步中所画的弧交于点D′;
(4)过点D画射线OB,则∠AOB=∠AOB.
说理:由作法得已知:OC=OC,OD=OD,CD=CD,
求证:∠AOB=∠AOB.
证明:在△OCD和△OCD中,
∴△OCD≌△OCD(SSS),
∴∠AOB=∠AOB(全等三角形的对应角相等),
故答案为:以C′为圆心,CD长为半径画弧与第二步中所画的弧交于点D′,SSS,全等三角形的对应角相等;
[小试牛刀]:如图,直线l′即为所求(方法不唯一),
;
[创新应用]:如图所示(答案不唯一),设计意图:书架中隐藏着无限宝藏,
.
【点睛】本题考查作图 应用与设计作图,全等三角形的判定和性质,平行线的判定等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
八年级数学上分层优化堂堂清
十二章 三角形
12.2三角形全等的判定第一课时
学习目标:
经历实验探究的过程,直观发现三边相等的两个三角形全等。会用直规作图法作“一条线段等于已知线段,一个角等于已知角”,提高动手操作能力。知道这样作图的理由。
能利用“SSS”进行有关的计算或证明。发展逻辑推理能力、计算能力和空间观念。
老师对你说:
知识点1 全等三角形的判定1:边边边(SSS)
文字:在两个三角形中,如果有三条边对应相等,那么这两个三角形全等.
图形:
符号:在与中,
证明的书写步骤:
①准备条件:证全等时要用的条件要先证好;②指明范围:写出在哪两个三角形中;
③摆齐根据:摆出三个条件用大括号括起来;④写出结论:写出全等结论.
注意:(1)说明两三角形全等所需的条件应按对应边的顺序书写.
(2)结论中所出现的边必须在所证明的两个三角形中.
知识点2 用尺规作一个角等于已知角
已知:∠AOB.求作: ∠A′O′B′=∠AOB.
作法:(1)以点O 为圆心,任意长为半径画弧,分别交OA,OB 于点C、D;
(2)画一条射线O′A′,以点O′为圆心,OC 长为半径画弧,交O′A′于点C′;
(3)以点C′为圆心,CD 长为半径画弧,与第2 步中所画的弧交于点D′;
(4)过点D′画射线O′B′,则∠A′O′B′=∠AOB.
知识点3 运用边边边定理证明和计算
运用“SSS”证明两个三角形全等主要是找边相等,边相等除了题目中已知的边相等外,还有一些相等边隐含在题设或图形中。
基础提升 教材核心知识点精练
知识点1 全等三角形的判定1:边边边(SSS)
【例1-1】如图,AC=FD,BC=ED,要利用“SSS”来判定△ABC和△FED全等时,下面的4个条件中:①AE=FB;②AB=FE;③AE=BE;④BF=BE,可利用的是( )
A.①或② B.②或③ C.①或③ D.①或④
【例1-1】如图,已知AD=BC,根据“SSS”,还需要一个条件________,可证明△ABC≌△BAD;
知识点2 用尺规作一个角等于已知角
【例2-1】用直尺和圆规画一个角等于已知角,是运用了“全等三角形的对应角相等”这一性质,其运用全等的方法是 (用字母写出).
【例2-2】如图,已知,请用尺规作图法,在边上求作一点P,使.
【例2-3】已知,为射线上一点,在内部,求作,使.(保留作图痕迹,不写作法)
知识点3 运用边边边定理证明和计算
【例3-1】如图1是小军制作的燕子风筝,燕子风筝的骨架图如图2所示,,,,,求.
【例3-2】已知:如图,.
(1)求证:;
(2)求的度数.
【例3-3】如图,已知AB=AC,AD=AE,BE=CD.
(1)求证:∠BAC=∠EAD;
(2)写出∠1,∠2,∠3之间的数量关系,并予以证明.
能力强化提升训练
1 .如图,已知,,,直线与,分别交于点,,且,,则的度数为___________.
2 .莆仙戏是现存最古老的地方戏剧种之一,被称为“宋元南戏的活化石”,2021年5月莆仙戏《踏伞行》获评为“2020年度国家舞台艺术精品创作扶持工程重点扶持剧目”.该剧中“油纸伞”无疑是最重要的道具,依伞设戏,情节新颖,结构巧妙,谱写了一曲美轮美奂、诗意盎然的传统戏曲乐歌.“油纸伞”的制作工艺十分巧妙.如图,伞圈D沿着伞柄滑动时,总有伞骨,,从而使得伞柄AP始终平分同一平面内两条伞骨所成的.为什么?
3.如图,已知,,求证.
4 .已知:如图1,在中,.求作:射线,使得.
下面是小明设计的尺规作图过程.
作法:如图2,
①以点为圆心,适当长为半径作弧,分别交,于,两点;
②以点为圆心,长为半径作弧,交的延长线于点;
③以点为圆心,长为半径作弧,两弧在内部交于点;
④作射线.所以射线就是所求作的射线.
根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:连接,.
,,.
__________,
__________,
(__________)(填推理的依据).
堂堂清
选择题(每小题4分,共32分)
1 .如图,在中,,D为中点,,则的度数是( )
A. B. C. D.
2 .工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M、N重合,过角尺顶点C作射线OC,由此作法便可得△NOC≌△MOC,其依据是( )
A.SSS B.SAS C.ASA D.AAS
3.如图,点C在的边OB上,尺规作图痕迹显示的是( )
A.作线段CE的垂直平分线 B.作的平分线
C.连接EN,则是等边三角形 D.作
4 .如图,,,则,其依据是( )
A. B. C. D.
5 .如图,已知,,是上两点且,若,,则的度数为( )
A. B. C. D.
6 .如图,AC=FD,BC=ED,要利用“SSS”来判定△ABC和△FED全等时,下面的4个条件中:①AE=FB;②AB=FE;③AE=BE;④BF=BE,可利用的是( )
A.①或② B.②或③ C.①或③ D.①或④
7 .如图,在△ABC和△DEB中,点C在BD边上,AC与BE交于F,若AB=DE,BC=EB,AC=DB,则∠ACB等于( )
A.∠D B.∠E C.2∠ABF D.∠AFB
8 .如图,点E、D分别在AB、AC上,若AB=AC,BE=CD,BD=EC,,,则∠BOC度数是( )
A. B. C. D.
二、填空题(每小题4分,共20分)
9 .如图,在和中,,,,则________ .
如图,若、,,,则_________.
11 .如图,用直尺和圆规作一个角等于已知角的过程中,依据全等三角形的性质可得,这里判断的依据是___________.
12 .2022年10月12日某中学八年级(4)班的同学在听了“天宫课堂”第三课,即我国航天员在中国空间站进行的太空授课后,组成数学兴趣小组进行了设计伞的实践活动.康康所在的小组依据全等三角形的判定设计了截面如图所示的伞骨结构,当伞完全打开后,测得,E,F分别是,的中点,,那么的依据是________
13 .如图,与交于点,①;②;③,请以①②③中的两个作为条件,另一个为结论,写出一个正确命题.
正确的命题是:____________________(格式:由××,得×;上述×用前面数字代号①②③表示).
三、解答题(共6小题,48分)
14 .(8分)已知:如图,点A,C,B,D都在一条直线上,AC=BD,AM=CN,BM=DN.求证:AM∥CN.
15 .(8分)如图,是的中点,.求证:.
16 .(8分)如图,在四边形ABCD中,,.求证:.
17 .(8分)如图,为线段外一点.
(1)求作直线,使得;(要求:尺规作图,不写作法,保留作图痕迹)
(2)根据作图,说明你画的直线符合要求的原因.
18 .如图,在四边形中,与相交于点E.
求证:.
19 .(8分)如图,已知,.求证:.
拓展培优*冲刺满分
1.已知,如图,,求证:
2.尺规作图之旅
下面是一副纯手绘的画作,其中用到的主要工具就是直尺和圆规,在数学中,我们也能通过尺规作图创造出许多带有美感的图形.
尺规作图起源于古希腊的数学课题,只允许使用圆规和直尺,来解决平面几何作图问题.
【作图原理】在两年的数学学习里中,我们认识了尺规作图,并学会用尺规作图完成一些作图问题,请仔细思考回顾,判断以下操作能否通过尺规作图实现,可以实现的画√,不能实现的 画×.
(1)过一点作一条直线.( )
(2)过两点作一条直线.( )
(3)画一条长为3㎝的线段.( )
(4)以一点为圆心,给定线段长为半径作圆.( )
【回顾思考】还记得我们用尺规作图完成的第一个问题吗?那就是“作一条线段等于已知线段”,接着,我们学习了使用尺规作图作线段的垂直平分线,作角平分线,过直线外一点作垂线……而这些尺规作图的背后都与我们学习的数学原理密切相关,下面是用尺规作一个角等于已知角的方法及说理,请补全过程.
已知:∠AOB.
求作:使
作法:(1)如图,以O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;
(2)画一条射线,以点为圆心,OC长为半径画弧,交于点;
(3)以点为圆心,____________________;
(4)过点画射线,则.
说理:由作法得已知:
求证:
证明:
( )
所以( )
【小试牛刀】请按照上面的范例,完成尺规作图并说理:过直线外一点作已知直线的平行线.
已知:直线与直线外一点A.
求作:过点A的直线,使得.
【创新应用】现实生活中许多图案设计都蕴含着数学原理,下面是一个常见商标的设计示意图.假设你拥有一家书店,请利用你手中的刻度尺和圆规,为你的书店设计一个图案.要求保留作图痕迹,并写出你的设计意图.
八年级数学上分层优化堂堂清
十二章 全等三角形
12.2三角形全等的判定第一课时(解析版)
学习目标:
经历实验探究的过程,直观发现三边相等的两个三角形全等。会用直规作图法作“一条线段等于已知线段,一个角等于已知角”,提高动手操作能力。知道这样作图的理由。
能利用“SSS”进行有关的计算或证明。发展逻辑推理能力、计算能力和空间观念。
老师对你说:
知识点1 全等三角形的判定1:边边边(SSS)
文字:在两个三角形中,如果有三条边对应相等,那么这两个三角形全等.
图形:
符号:在与中,
证明的书写步骤:
①准备条件:证全等时要用的条件要先证好;②指明范围:写出在哪两个三角形中;
③摆齐根据:摆出三个条件用大括号括起来;④写出结论:写出全等结论.
注意:(1)说明两三角形全等所需的条件应按对应边的顺序书写.
(2)结论中所出现的边必须在所证明的两个三角形中.
知识点2 用尺规作一个角等于已知角
已知:∠AOB.求作: ∠A′O′B′=∠AOB.
作法:(1)以点O 为圆心,任意长为半径画弧,分别交OA,OB 于点C、D;
(2)画一条射线O′A′,以点O′为圆心,OC 长为半径画弧,交O′A′于点C′;
(3)以点C′为圆心,CD 长为半径画弧,与第2 步中所画的弧交于点D′;
(4)过点D′画射线O′B′,则∠A′O′B′=∠AOB.
知识点3 运用边边边定理证明和计算
运用“SSS”证明两个三角形全等主要是找边相等,边相等除了题目中已知的边相等外,还有一些相等边隐含在题设或图形中。
基础提升 教材核心知识点精练
知识点1 全等三角形的判定1:边边边(SSS)
【例1-1】如图,AC=FD,BC=ED,要利用“SSS”来判定△ABC和△FED全等时,下面的4个条件中:①AE=FB;②AB=FE;③AE=BE;④BF=BE,可利用的是( )
A.①或② B.②或③ C.①或③ D.①或④
【答案】A
【分析】根据全等三角形的SSS判定条件解答即可.
【详解】解:∵AE=FB,
∴AE+BE=FB+BE,
∴AB=FE,
在△ABC和△FED中,
,
∴△ABC≌△FED(SSS),
∵AE=BE和BF=BE推不出AB=FE,
∴可利用的是①或②,
故选:A.
【点评】本题考查全等三角形的判定,熟练掌握全等三角形的判定方法是解答的关键.
【例1-1】如图,已知AD=BC,根据“SSS”,还需要一个条件________,可证明△ABC≌△BAD;
【答案】DB=CA
【解析】图形中隐含条件AB=BA,找出第三边BD和AC即可;
在△ABC和△BAD中 ,∴△ABC≌△BAD(SSS)
【点评】本题考查全等三角形的判定,熟练掌握全等三角形的判定方法是解答的关键.
知识点2 用尺规作一个角等于已知角
【例2-1】用直尺和圆规画一个角等于已知角,是运用了“全等三角形的对应角相等”这一性质,其运用全等的方法是 (用字母写出).
【分析】根据用直尺和圆规画一个角等于已知角的过程很容易看出所得两个三角形三边对应相等.
【解答】
解:①设已知角的顶点为O,以O为圆心,任意长度为半径画圆,交角两边为A,B两点;
②用直尺画一条射线,端点为M,以M为圆心,用同样的半径画圆,该圆为圆M,交射线为C点;
③以A为圆心,以AB为半径画圆,然后以C点为圆心,以同样的半径画圆,交圆M于D,E两点,随意连MD或者ME;得到的∠CMD就是所求的角;由以上作角过程不难看出有三个对应边相等.
∴证明全等的方法是SSS.故答案为:SSS.
【点评】本题考查的关键是作角的过程,作角过程中所产生的条件就是证明全等的条件.
【例2-2】如图,已知,请用尺规作图法,在边上求作一点P,使.
【答案】见解析
【详解】根据作与已知角相等的角的尺规作图方法作图即可.
【分析】解:如图所示,点P即为所求.
【点评】本题主要考查了尺规作图—作与已知角相等的角,熟知相关作图方法是解题的关键.
【例2-3】已知,为射线上一点,在内部,求作,使.(保留作图痕迹,不写作法)
【答案】图见解析
【分析】根据作角等于已知角的方法,进行作图即可.
【详解】解:如图所示,即为所求;
【点评】本题考查作角等于已知角.熟练掌握尺规作图方法,是解题的关键.
知识点3 运用边边边定理证明和计算
【例3-1】如图1是小军制作的燕子风筝,燕子风筝的骨架图如图2所示,,,,,求.
【答案】
【分析】根据题意,直接根据证明,再根据全等三角形对应角相等,即可求解.
【详解】解:在和中,
,
∴,
∴.
【点评】本题主要考查了三角形全等的判定和性质,解题的关键是掌握全等三角形的判定方法以及全等三角形对应边相等,对应角相等.判定三角形全等的方法是.
【例3-2】已知:如图,.
(1)求证:;
(2)求的度数.
【答案】(1)证明见解析
(2)
【分析】(1)直接利用证明即可;
(2)先根据全等三角形的性质得到,再利用三角形外角的性质求解即可.
【详解】(1)证明:在和中,
,
∴;
(2)解:∵,
∴,
∴.
【点评】本题主要考查了全等三角形的性质与判定,三角形外角的性质,熟知全等三角形的性质与判定条件是解题的关键.
【例3-3】如图,已知AB=AC,AD=AE,BE=CD.
(1)求证:∠BAC=∠EAD;
(2)写出∠1,∠2,∠3之间的数量关系,并予以证明.
【答案】(1)见解析;(2)∠3=∠1+∠2,见解析
【分析】(1)根据SSS证△BAE≌△CAD,推出∠BAE=∠CAD即可;
(2)根据全等三角形性质推出∠1=∠BAE,∠2=∠ABE,代入∠3=∠BAE+∠ABE求出即可.
【详解】(1)证明:在△ABE和△ACD中,
∵AB=AC,AD=AE,BE=CD
∴△ABE≌△ACD(SSS),
∴∠BAE=∠CAD.
∴∠BAE+ EAC=∠CAD+ EAC .
∴∠BAC=∠EAD.
(2) ∠3=∠1+∠2;
理由如下:由图中知,
∠3=∠ABE+∠BAE
又由(1)中知△ABE≌△ACD,
∴ ∠ABE=∠2 , ∠BAE=∠1
∴ ∠3=∠1+∠2
【点评】本题考查了全等三角形的性质和判定,三角形外角的性质,注意:全等三角形的对应角相等.
能力强化提升训练
1 .如图,已知,,,直线与,分别交于点,,且,,则的度数为___________.
【答案】
【分析】根据SSS得到,进而得到,,再结合对顶角相等,可得,最后再利用角的和差即可求解.
【详解】解:∵,,,
,
,,
与是对顶角,
∴,
∴,
∴,
∴,
故答案为:10°.
【点评】本题考查全等三角形的判定与性质,对顶角的性质、角的和差计算等内容,识别出与这一组对顶角,得到的度数是解题的关键.
2 .莆仙戏是现存最古老的地方戏剧种之一,被称为“宋元南戏的活化石”,2021年5月莆仙戏《踏伞行》获评为“2020年度国家舞台艺术精品创作扶持工程重点扶持剧目”.该剧中“油纸伞”无疑是最重要的道具,依伞设戏,情节新颖,结构巧妙,谱写了一曲美轮美奂、诗意盎然的传统戏曲乐歌.“油纸伞”的制作工艺十分巧妙.如图,伞圈D沿着伞柄滑动时,总有伞骨,,从而使得伞柄AP始终平分同一平面内两条伞骨所成的.为什么?
【答案】见解析
【分析】利用SSS证明,即可得到,由此证得结论.
【详解】证明:∵在和中,
,∴,∴,即AP平分.
【点评】此题考查了全等三角形的判定及性质,熟记全等三角形的判定定理是解题的关键.
如图,已知,,求证.
【答案】见解析
【分析】利用证明,根据全等三角形的性质可得,,再由,,即可得出
【详解】解:在和中,
,
∴,
∴,,
又∵,,
∴
【点评】本题主要考查全等三角形的判定和性质,熟练掌握全等三角形的判定和性质是解题的关键.
4 .已知:如图1,在中,.求作:射线,使得.
下面是小明设计的尺规作图过程.
作法:如图2,
①以点为圆心,适当长为半径作弧,分别交,于,两点;
②以点为圆心,长为半径作弧,交的延长线于点;
③以点为圆心,长为半径作弧,两弧在内部交于点;
④作射线.所以射线就是所求作的射线.
根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:连接,.
,,.
__________,
__________,
(__________)(填推理的依据).
【答案】(1)见解析;(2),,同位角相等两直线平行
【分析】(1)根据要求作出图形即可.
(2)利用全等三角形的性质证明即可.
【详解】解:(1)如图,射线即为所求作.
(2)连接,.
,,.
,
,
(同位角相等两直线平行).
故答案为:,,同位角相等两直线平行.
【点评】本题考查作图-复杂作图,全等三角形的判定和性质,平行线的判定等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
堂堂清
选择题(每小题4分,共32分)
1 .如图,在中,,D为中点,,则的度数是( )
A. B. C. D.
【答案】A
【分析】证明得到,,即可利用三角形内角和定理求出答案.
【详解】解:∵D为中点,
∴,
又∵,
∴,
∴,,
又∵,
∴,
∴,
故选A.
【点评】本题主要考查了全等三角形的性质与判定,三角形内角和定理,证明是解题的关键.
2 .工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M、N重合,过角尺顶点C作射线OC,由此作法便可得△NOC≌△MOC,其依据是( )
A.SSS B.SAS C.ASA D.AAS
答案 A
解析 ∵在△ONC和△OMC中,∴△MOC≌△NOC(SSS),
∴∠BOC=∠AOC,故选:A.
3.如图,点C在的边OB上,尺规作图痕迹显示的是( )
A.作线段CE的垂直平分线 B.作的平分线
C.连接EN,则是等边三角形 D.作
【答案】D
【分析】根据作图得出△ODM≌△CEN(SSS),得出∠MAD=∠NCE,得出OM∥CN即可.
【详解】解:连结EN ,
在△ODM和△CEN中,
,
∴△ODM≌△CEN(SSS),
∴∠MAD=∠NCE,
∴OM∥CN,
故选D.
【点评】本题考查尺规作图,掌握基本作图,三角形全等判定与性质,平行线的判定是解题关键.
4 .如图,,,则,其依据是( )
A. B. C. D.
【答案】C
【分析】由题可得,两个三角形三条对应边相等,则判断其全等依据为边边边.
解:在和中,
所以
故选:C
【点拨】本题考查三角形全等的判定,找到对应条件是解题的关键.
5 .如图,已知,,是上两点且,若,,则的度数为( )
A. B. C. D.
【答案】D
【分析】先证,得,再证,得,然后由三角形的外角性质即可得出结论.
【详解】解:在和中,
,
∴,
∴,
在和中,
,
∴,
∴,
∵,
∴.
故选:D.
【点评】本题主要考查了全等三角形的判定与性质以及三角形的外角性质等知识,熟练掌握全等三角形的判定与性质是解题的关键.
6 .如图,AC=FD,BC=ED,要利用“SSS”来判定△ABC和△FED全等时,下面的4个条件中:①AE=FB;②AB=FE;③AE=BE;④BF=BE,可利用的是( )
A.①或② B.②或③ C.①或③ D.①或④
【答案】A
【分析】根据全等三角形的SSS判定条件解答即可.
解:∵AE=FB,
∴AE+BE=FB+BE,
∴AB=FE,
在△ABC和△FED中,
,
∴△ABC≌△FED(SSS),
∵AE=BE和BF=BE推不出AB=FE,
∴可利用的是①或②,
故选:A.
【点拨】本题考查全等三角形的判定,熟练掌握全等三角形的判定方法是解答的关键.
7 .如图,在△ABC和△DEB中,点C在BD边上,AC与BE交于F,若AB=DE,BC=EB,AC=DB,则∠ACB等于( )
A.∠D B.∠E C.2∠ABF D.∠AFB
D
【分析】先根据SSS定理得出△ABC≌△DEB(SSS),故∠ACB=∠EBD,再根据∠AFB是△BFC的外角,可知∠AFB=∠ACB+∠EBD,由此可得出∠AFB=2∠ACB,故可得出结论.
解:在△ABC与△DEB中, ,
∴△ABC≌△DEB(SSS),
∴∠ACB=∠EBD.
∵∠AFB是△BFC的外角,
∴∠AFB=∠ACB+∠EBD,
∴∠AFB=2∠ACB,即∠AFB=∠ACB,
故选:D.
【点拨】本题考查的是全等三角形的判定与性质,熟知全等三角形的判定定理是解答此题的关键.
8 .如图,点E、D分别在AB、AC上,若AB=AC,BE=CD,BD=EC,,,则∠BOC度数是( )
A. B. C. D.
【答案】D
【分析】先利用SSS证明,利用全等三角形的性质推出,连接AO,延长至F,利用三角形外角的性质可得,由此可解.
解:∵AB=AC,BD=EC,
∴,即,
在和中,
,
∴,
∴,
如图,连接AO,延长AO至F,
根据三角形外角的性质可得,,,
∴,
故选:D.
【点拨】本题考查全等三角形的判定与性质,以及三角形外角的性质,证明是解题的关键.
二、填空题(每小题4分,共20分)
9 .如图,在和中,,,,则________ .
130
【分析】证明△ABC≌△ADC即可.
解:∵,,AC=AC,
∴△ABC≌△ADC,
∴∠D=∠B=130°,
故答案为:130.
【点拨】本题考查了全等三角形的判定和性质,掌握判定定理是解题关键.
如图,若、,,,则_________.
【分析】连接并延长至点E,先证明,得到,,再利用三角形外角的性质,求得,即可求出的度数.
解:如图,连接并延长至点E,
在和中,
,
,
,,
,,
故答案为:.
【点拨】本题考查了全等三角形的判定和性质,三角形外角的性质,作辅助线构造全等三角形是解题关键.
11 .如图,用直尺和圆规作一个角等于已知角的过程中,依据全等三角形的性质可得,这里判断的依据是___________.
【答案】
【分析】首先要清楚画图的步骤,步骤是以O为圆心,任意长为半径用圆规画弧,分别交于点;任意画一点,画射线,以为圆心,长为半径画弧交于点,以为圆心,长为半径画弧,可确定点的位置,过点画射线,就是与相等的角;则通过作图我们可以得到,接下来结合全等三角形的判定,即可解答.
解:根据作法可知,
∴,
故答案为:.
【点拨】本题考查尺规作图,解答本题的关键是掌握用尺规作一个角等于已知角的步骤,也考查了全等三角形的判定.
12 .2022年10月12日某中学八年级(4)班的同学在听了“天宫课堂”第三课,即我国航天员在中国空间站进行的太空授课后,组成数学兴趣小组进行了设计伞的实践活动.康康所在的小组依据全等三角形的判定设计了截面如图所示的伞骨结构,当伞完全打开后,测得,E,F分别是,的中点,,那么的依据是________
【答案】SSS
【分析】由E,F分别是,的中点,,得出;根据三边对应相等,证明.
解:∵E,F分别是,的中点,
∴
在与中
∴
故填SSS
【点拨】本题考查全等三角形的判定,解题的关键是熟练掌握全等三角形的判定定理.
13 .如图,与交于点,①;②;③,请以①②③中的两个作为条件,另一个为结论,写出一个正确命题.
正确的命题是:____________________(格式:由××,得×;上述×用前面数字代号①②③表示).
【答案】(1)由①③,得②;或由②③,得①;
【分析】分两种情形,利用全等三角形的判定和性质分别证明即可.
解:正确的命题是:由①③,得②;或由②③,得①;
证明:由①③,得②,
若,,
连接,
在和中,
,
,
;
或由②③,得①,
若,,
在和中,
,
,
,,
.
【点拨】本题考查命题,全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题.
三、解答题(共6小题,48分)
14 .(8分)已知:如图,点A,C,B,D都在一条直线上,AC=BD,AM=CN,BM=DN.求证:AM∥CN.
【答案】证明见详解.
【分析】首先根据可得,再加上条件 可利用SSS定理证明≌即可.
【详解】证明:
即
在和中,
∴≌(SSS),
∴∠A=∠NCD,
∴AM∥CN.
【点评】本题考查三角形全等判定,掌握三角形全等判定定理与方法是解题关键
15 .(8分)如图,是的中点,.求证:.
见分析
【分析】根据是的中点,得到,再利用证明两个三角形全等.
解:证明:是的中点,
,
在和中,
,
【点拨】本题考查了线段中点,三角形全等的判定,其中对三角形判定条件的确定是解决本题的关键.
16 .(8分)如图,在四边形ABCD中,,.求证:.
【答案】证明见解析
【分析】连接 证明再利用全等三角形的性质可得结论.
【详解】解:连接
四边形ABCD中,,,
【点评】本题考查的是全等三角形的判定与性质,构建全等三角形,利用证明三角形全等是解题的关键.
17 .(8分)如图,为线段外一点.
(1)求作直线,使得;(要求:尺规作图,不写作法,保留作图痕迹)
(2)根据作图,说明你画的直线符合要求的原因.
【答案】(1)见解析;(2)见解析
【分析】(1)先过点B作射线BE,且BE过点C,然后作,则直线即为所求的平行线;
(2)利用同位角相等,两直线平行即可判断.
【详解】解:(1)先过点B作射线BE,且BE过点C,然后作,
如图,直线即为所求的平行线;
(2)由作图可知,,
所以,
所以所画直线符合要求.
【点评】本题主要考查了尺规作图——作一个角等于已知角,平行线的判定,熟练掌握平行线的同位角相等,两直线平行是解题的关键.
18 .如图,在四边形中,与相交于点E.
求证:.
见分析
【分析】直接利用SSS证明△ACD≌△BDC,即可证明.
解:在△ACD和△BDC中,
,
∴△ACD≌△BDC(SSS),
∴∠DAC=∠CBD.
【点拨】本题考查了全等三角形的判定和性质,解题的关键是根据题意灵活运用SSS的方法.
19 .(8分)如图,已知,.求证:.
见详解.
【分析】根据SSS定理推出△ADB≌△BCA即可证明.
解:证明:在△ADB和△BCA中,
∴△ADB≌△BCA(SSS),
∴.
【点拨】本题考查了全等三角形的性质和判定,能正确进行推理证明全等是解此题的关键.
拓展培优*冲刺满分
1.已知,如图,,求证:
【答案】见详解
【分析】连接,证明即可求得答案.
【详解】证明:连接,如图所示,
∵,,,
∴,
∴;
【点评】本题考查了几何问题,正确作出辅助线是解题关键.
2.尺规作图之旅
下面是一副纯手绘的画作,其中用到的主要工具就是直尺和圆规,在数学中,我们也能通过尺规作图创造出许多带有美感的图形.
尺规作图起源于古希腊的数学课题,只允许使用圆规和直尺,来解决平面几何作图问题.
【作图原理】在两年的数学学习里中,我们认识了尺规作图,并学会用尺规作图完成一些作图问题,请仔细思考回顾,判断以下操作能否通过尺规作图实现,可以实现的画√,不能实现的 画×.
(1)过一点作一条直线.( )
(2)过两点作一条直线.( )
(3)画一条长为3㎝的线段.( )
(4)以一点为圆心,给定线段长为半径作圆.( )
【回顾思考】还记得我们用尺规作图完成的第一个问题吗?那就是“作一条线段等于已知线段”,接着,我们学习了使用尺规作图作线段的垂直平分线,作角平分线,过直线外一点作垂线……而这些尺规作图的背后都与我们学习的数学原理密切相关,下面是用尺规作一个角等于已知角的方法及说理,请补全过程.
已知:∠AOB.
求作:使
作法:(1)如图,以O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;
(2)画一条射线,以点为圆心,OC长为半径画弧,交于点;
(3)以点为圆心,____________________;
(4)过点画射线,则.
说理:由作法得已知:
求证:
证明:
( )
所以( )
【小试牛刀】请按照上面的范例,完成尺规作图并说理:过直线外一点作已知直线的平行线.
已知:直线与直线外一点A.
求作:过点A的直线,使得.
【创新应用】现实生活中许多图案设计都蕴含着数学原理,下面是一个常见商标的设计示意图.假设你拥有一家书店,请利用你手中的刻度尺和圆规,为你的书店设计一个图案.要求保留作图痕迹,并写出你的设计意图.
【答案】【作图原理】(1)√;(2)√;(3)×;(4)√;【回顾思考】作法:以点为圆心,以CD为半径画弧,与第二步中所画的弧相交于;说理:SSS,全等三角形对应角相等;【小试牛刀】答案见解析;【创新应用】答案见解析.
【分析】[作图原理]根据五种基本作图判断即可;
[回顾思考]利用全等三角形的判定解决问题即可;
[小试牛刀]利用同位角相等两直线平行解决问题即可;
[创新应用]答案不唯一,画出图形,说明设计意图即可.
【详解】解:[作图原理]:(1)过一点作一条直线.可以求作;
(2)过两点作一条直线.可以求作;
(3)画一条长为3cm的线段.不可以求作;
(4)以一点为圆心,给定线段长为半径作圆.可以求作;
故答案为:√,√,×,√;
[回顾思考]:作法:(1)如图,以O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;
(2)画一条射线OA,以点O为圆心,OC长为半径画弧,交OA于点C;
(3)以点C为圆心,以C′为圆心,CD长为半径画弧与第二步中所画的弧交于点D′;
(4)过点D画射线OB,则∠AOB=∠AOB.
说理:由作法得已知:OC=OC,OD=OD,CD=CD,
求证:∠AOB=∠AOB.
证明:在△OCD和△OCD中,
∴△OCD≌△OCD(SSS),
∴∠AOB=∠AOB(全等三角形的对应角相等),
故答案为:以C′为圆心,CD长为半径画弧与第二步中所画的弧交于点D′,SSS,全等三角形的对应角相等;
[小试牛刀]:如图,直线l′即为所求(方法不唯一),
;
[创新应用]:如图所示(答案不唯一),设计意图:书架中隐藏着无限宝藏,
.
【点睛】本题考查作图 应用与设计作图,全等三角形的判定和性质,平行线的判定等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
