八年级数学上分层优化堂堂清(3)12.2全等三角形的判定第二课时(含解析)
文档属性
| 名称 | 八年级数学上分层优化堂堂清(3)12.2全等三角形的判定第二课时(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-20 15:51:09 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
八年级数学上分层优化堂堂清
十二章 全等三角形
12.2三角形全等的判定第二课时
学习目标:
1.能够利用尺规正确的画出一个与给定三角形满足SAS条件的全等的三角形,能准确叙述SAS.
2.能够利用SAS进行简单的几何推理(计算或证明)
3.能够利用SAS进行较复杂的几何推理(计算或证明)
4.能画图说明满足SSA条件的两个三角形不一定全等.能够综合利用SSS、SAS进行复杂的几何推理.
老师对你说:
知识点1 全等三角形的判定2:边角边(SAS)
三角形全等的判定2:边角边(SAS)
文字:在两个三角形中,如果有两条边及它们的夹角对应相等,那么这两个三角形全等;
图形:
符号:在与中,.
知识点2 利用SAS进行推理证明
①用“SAS”判定两个三角形全等时,必须满足“两边及它们的夹角”这一条件,在书写时,一般按“边角边”的顺序.
②有两边和其中一角对应相等的两个三角形不一定全等
知识点3 综合利用SSS、SAS进行复杂的几何推理.
证明三角形全等的“两个条件”(1)直接条件:已知中直接给出的边(角)对应相等,
隐含条件:已知中没有给出,但通过读图得到的条件,如公共边、公共角、对顶角。
“SAS”判定方法证明两个三角形全等及进行简单的应用.
1.证明线段相等或者角相等时,常常通过证明它们是全等三角形的对应边或对应角来解决.
2判断三角形全等时,注意两边与其中一边的对角相等的两个三角形不一定全等.解题时要根据已知条件的位置来考虑,只具备SSA时是不能判定三角形全等的.
基础提升 教材核心知识点精练
知识点1 全等三角形的判定2:边角边(SAS)
【例1-1】如图,AD⊥AB,AE⊥AC,AD=AB,AE=AC,则判定△ADC≌△ABE的根据是____.
【例1-2】如图,工人师傅设计了一种测零件内径的卡钳,卡钳交叉点O为、的中点,只要量出的长度,就可以道该零件内径的长度.依据的数学基本事实是( )
A.两边及其夹角分别相等的两个三角形全等 B.两角及其夹边分别相等的两个三角形全等
C.两余直线被一组平行线所截,所的对应线段成比例 D.两点之间线段最短
【例1-3】如图,与相交于点O,,不添加辅助线,判定的依据是( )
A. B. C. D.
知识点2 利用SAS进行推理证明
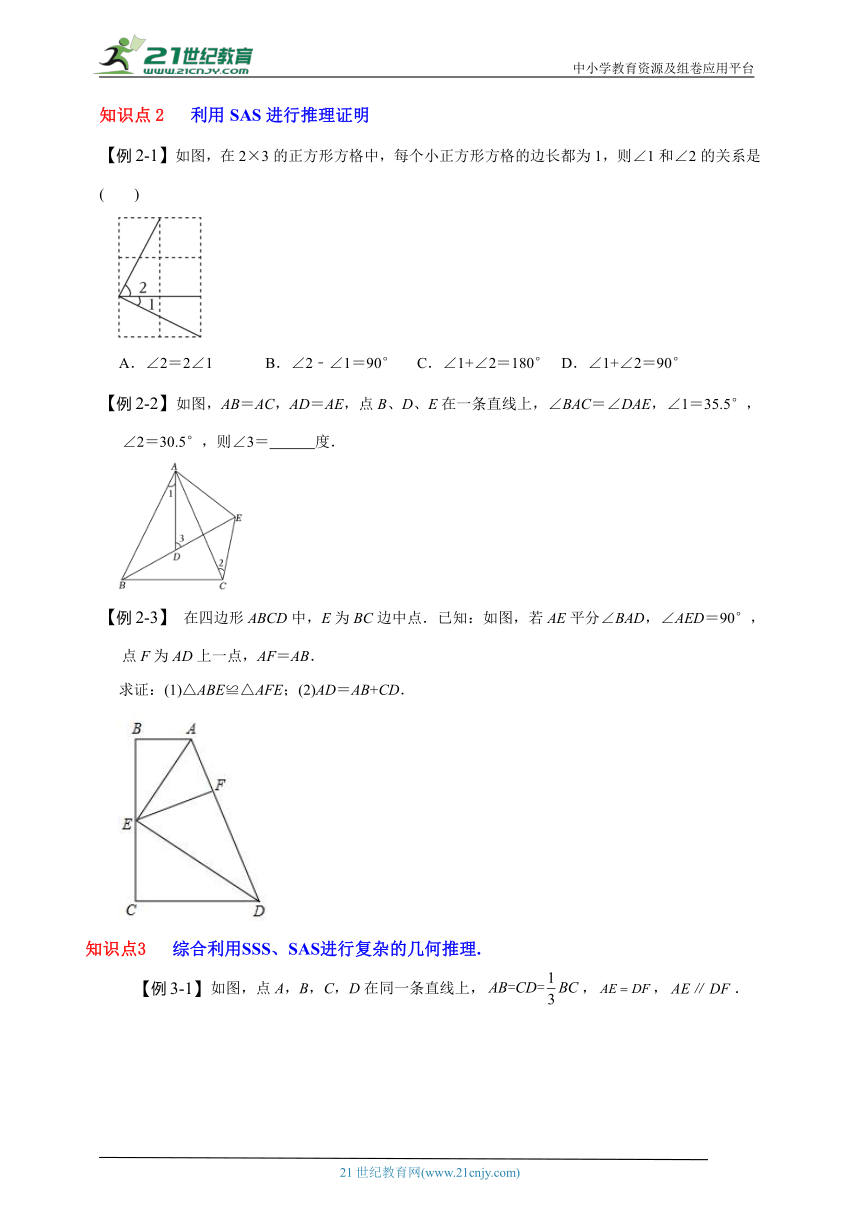
【例2-1】如图,在2×3的正方形方格中,每个小正方形方格的边长都为1,则∠1和∠2的关系是( )
A.∠2=2∠1 B.∠2﹣∠1=90° C.∠1+∠2=180° D.∠1+∠2=90°
【例2-2】如图,AB=AC,AD=AE,点B、D、E在一条直线上,∠BAC=∠DAE,∠1=35.5°,∠2=30.5°,则∠3= 度.
【例2-3】 在四边形ABCD中,E为BC边中点.已知:如图,若AE平分∠BAD,∠AED=90°,点F为AD上一点,AF=AB.
求证:(1)△ABE≌△AFE;(2)AD=AB+CD.
知识点3 综合利用SSS、SAS进行复杂的几何推理.
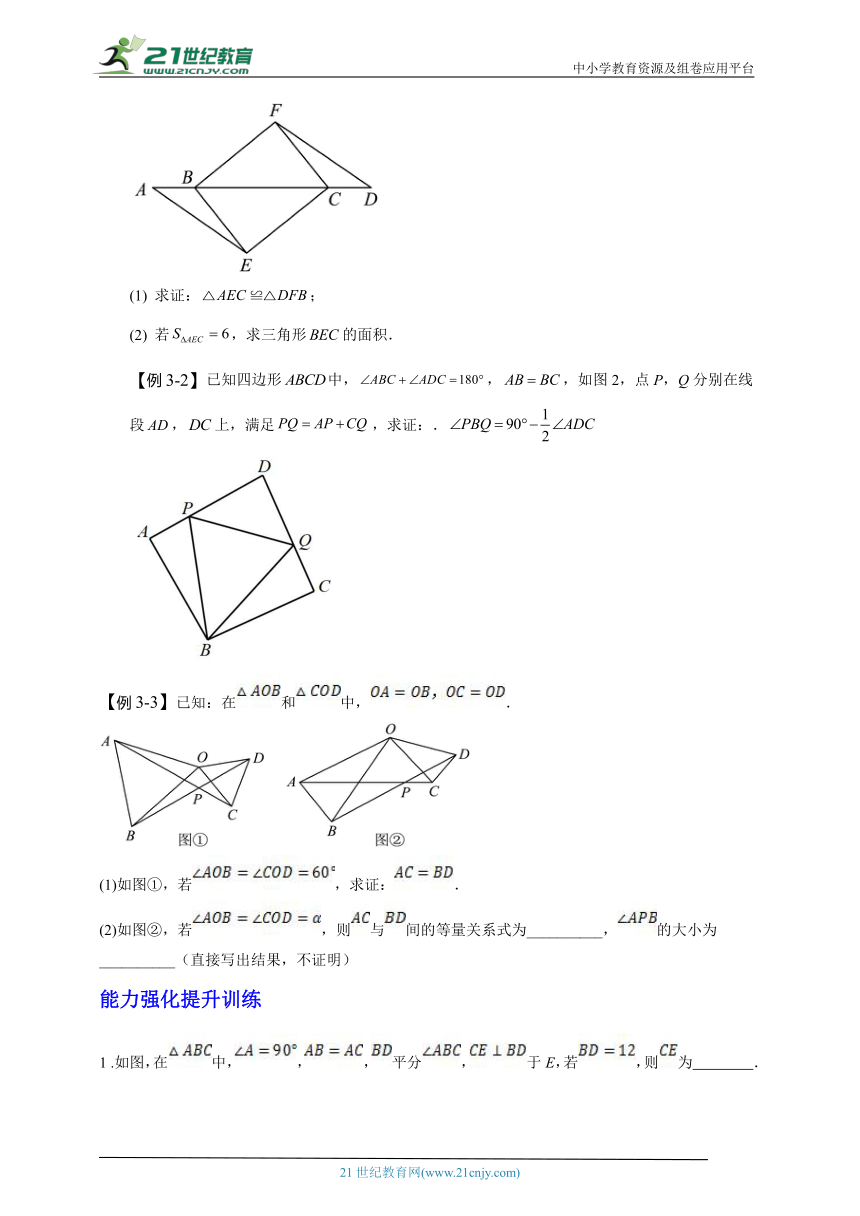
【例3-1】如图,点A,B,C,D在同一条直线上,,,.
求证:;
若,求三角形的面积.
【例3-2】已知四边形中,,,如图2,点P,Q分别在线段,上,满足,求证:.
【例3-3】已知:在和中,.
(1)如图①,若,求证:.
(2)如图②,若,则与间的等量关系式为__________,的大小为__________(直接写出结果,不证明)
能力强化提升训练
1 .如图,在中,,,平分,于E,若,则为 .
如图,在中,,分别是,边上的高,在上取一点D,使,在射线上取一点G,使,连结,.若,,则的度数为 .
如图,在中,,.过点作,垂足为,延长至点.使.在边上截取,连接.求证:.
4 .如图,在中,,分别是,边上的高,在上载取,延长至点使,连接,.
(1)求证:;
(2)求的度数;
堂堂清
选择题(每小题4分,共32分)
1 .如图中全等的三角形是( )
A.①和② B.①和③ C.②和③ D.②和④
2 .如图,在2×3的正方形方格中,每个小正方形方格的边长都为1,则∠1和∠2的关系是( )
A.∠2=2∠1 B.∠2﹣∠1=90° C.∠1+∠2=180° D.∠1+∠2=90°
3 .如图,有一池塘,要测量池塘两端A,B的距离时,可先在平地上取一个可以直接到达A和B的点C.连接AC并延长到D,使CD=CA.连接BC并延长到E,使CE=CB.可证明△EDC≌△BAC,从而得到ED=AB,则测得ED的长就是两点A,B的距离.判定△EDC≌△BAC的依据是( )
A.“边边边” B.“角边角” C.“角角边” D.“边角边”
4 .如图,小明把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是( )
A.带①去 B.带②去 C.带③去 D.①②③都带去
5 .如图,是和的公共边,下列条件不能判定的是( )
A., B.,
C., D.,
6 .如图,已知,,,,,则的度数为( )
A. B. C. D.
7 .如图,把长短确定的两根木棍AB、AC的一端固定在A处,和第三根木棍BM摆出△ABC,木棍AB固定,木棍AC绕A转动,得到△ABD,这个实验说明( )
A.△ABC与△ABD不全等
B.有两边分别相等的两个三角形不一定全等
C.两边和它们的夹角分别相等的两个三角形全等
D.有两边和其中一边的对角分别相等的两个三角形不一定全等
8 .如图,在正方形方格中,每个小正方形的边长都是一个单位长度,点均在小正方形方格的顶点上,线段交于点,若,则等于( )
A. B. C. D.
二、填空题(每小题4分,共20分)
9 .如图,已知AB∥CF,点E为DF的中点,若AB=9 cm,CF=5 cm,则BD=____cm.
10 如图,在中,,,,分别在,,上,且,,,则的度数是_____.(用含的代数式表示)
11 .如图,在中,,,是边上的中线,则的取值范围是________
12 .如图,△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,D,E在同一条直线上,若∠CAE+∠ACE+∠ADE=130°,则∠ADE的度数为________°.
13 .如图,在△ABC中,AB=6,BC=5,AC=4,AD平分∠BAC交BC于点D,在AB上截取AE=AC,则△BDE的周长为____________
三、解答题(共6小题,48分)
14 .(8分)如图,.求证:.
15 .(8分)如图,在中,,.过点作,垂足为,延长至点.使.在边上截取,连接.求证:.
16 .(8分)如图,在和中,,,,连接,C、D、E三点在同一条直线上,连接.
(1)求证:;
(2)判断与的位置关系并说明理由.
17 .(8分).如图,在△ABC和△AEF中,AB=AC,AE=AF,∠BAC=∠EAF,BE与CF交于点O,与AC交于点D.
(1)求证:BE=CF;
(2)若∠BAC=80°,求∠BOF的度数.
18 .(8分)如图,在梯形ABCD中,AD∥BC,AE平分∠BAD,BE平分∠ABC,且AE、BE交CD于点E.试说明AD=AB﹣BC的理由.
19 .(8分)如图,在四边形中,于,,.求证:(1);(2).
拓展培优*冲刺满分
如图,已知长方形ABCD的边长,,点E在边AB上,,如果点P从点B出发在线段BC上向点C运动,同时,点Q在线段DC上从点D向点C运动,已知点P的运动速度是2cm/s,则经过______s,与全等.
2 .问题发现:如图1,已知为线段上一点,分别以线段,为直角边作等腰直角三角形,,,,连接,,线段,之间的数量关系为______;位置关系为_______.
拓展探究:如图2,把绕点逆时针旋转,线段,交于点,则与之间的关系是否仍然成立?请说明理由.
3 .(1)阅读理解:如图1,在中,若,.求边上的中线的取值范围.解决此问题可以用如下方法:延长到点,使,再连接(或将绕着点逆时针旋转得到),把,,集中在中,利用三角形三边的关系即可判断中线的取值范围是______;
(2)问题解决:如图2,在中,是边上的中点,于点,交于点,交于点,连接,求证:;
(3)问题拓展:如图3,在四边形中,,,,以为顶点作一个角,角的两边分别交,于,两点,连接,探索线段,,之间的数量关系,并加以证明.
八年级数学上分层优化堂堂清
十二章 全等三角形
12.2三角形全等的判定第二课时(解析版)
学习目标:
1.能够利用尺规正确的画出一个与给定三角形满足SAS条件的全等的三角形,能准确叙述SAS.
2.能够利用SAS进行简单的几何推理(计算或证明)
3.能够利用SAS进行较复杂的几何推理(计算或证明)
4.能画图说明满足SSA条件的两个三角形不一定全等.能够综合利用SSS、SAS进行复杂的几何推理.
老师对你说:
知识点1 全等三角形的判定2:边角边(SAS)
三角形全等的判定2:边角边(SAS)
文字:在两个三角形中,如果有两条边及它们的夹角对应相等,那么这两个三角形全等;
图形:
符号:在与中,.
知识点2 利用SAS进行推理证明
①用“SAS”判定两个三角形全等时,必须满足“两边及它们的夹角”这一条件,在书写时,一般按“边角边”的顺序.
②有两边和其中一角对应相等的两个三角形不一定全等
知识点3 综合利用SSS、SAS进行复杂的几何推理.
证明三角形全等的“两个条件”(1)直接条件:已知中直接给出的边(角)对应相等,
隐含条件:已知中没有给出,但通过读图得到的条件,如公共边、公共角、对顶角。
“SAS”判定方法证明两个三角形全等及进行简单的应用.
1.证明线段相等或者角相等时,常常通过证明它们是全等三角形的对应边或对应角来解决.
2判断三角形全等时,注意两边与其中一边的对角相等的两个三角形不一定全等.解题时要根据已知条件的位置来考虑,只具备SSA时是不能判定三角形全等的.
基础提升 教材核心知识点精练
知识点1 全等三角形的判定2:边角边(SAS)
【例1-1】如图,AD⊥AB,AE⊥AC,AD=AB,AE=AC,则判定△ADC≌△ABE的根据是____.
【答案】SAS
【解析】∵AD⊥AB,AE⊥AC,∴∠DAB=∠EAC=90°,∴∠DAB+∠BAC=∠EAC+∠BAC,即:∠DAC=∠BAE,
在△ADC和△ABE中,AD=AB,∠DAC=∠BAE,AE=AC,
∴△ADC≌△ABE(SAS),故填:SAS.
【点评】本题考查全等三角形的判定和性质、三角形的外角的性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型
【例1-2】如图,工人师傅设计了一种测零件内径的卡钳,卡钳交叉点O为、的中点,只要量出的长度,就可以道该零件内径的长度.依据的数学基本事实是( )
A.两边及其夹角分别相等的两个三角形全等 B.两角及其夹边分别相等的两个三角形全等
C.两余直线被一组平行线所截,所的对应线段成比例 D.两点之间线段最短
【答案】A
【分析】根据题意易证,根据证明方法即可求解.
解:O为、的中点,
,,
(对顶角相等),
在与中,
,
,
,
故选:A.
【点拨】本题考查了全等三角形的证明,正确使用全等三角形的证明方法是解题的关键.
【例1-3】如图,与相交于点O,,不添加辅助线,判定的依据是( )
A. B. C. D.
【答案】B
【分析】根据,,正好是两边一夹角,即可得出答案.
解:∵在△ABO和△DCO中,,
∴,故B正确.
故选:B.
【点拨】本题主要考查了全等三角形的判定,熟练掌握两边对应相等,且其夹角也对应相等的两个三角形全等,是解题的关键.
知识点2 利用SAS进行推理证明
【例2-1】如图,在2×3的正方形方格中,每个小正方形方格的边长都为1,则∠1和∠2的关系是( )
A.∠2=2∠1 B.∠2﹣∠1=90° C.∠1+∠2=180° D.∠1+∠2=90°
答案 D
解析 如图:
由题意得:AC=BD=2,BC=DE=1,∠ACB=∠BDE=90°,
∴∠1+∠BED=90°,
在△ABC和△BED中,,∴△ABC≌△BED(SAS),
∴∠2=∠BED,
∴∠1+∠2=90°,
故选:D.
【例2-2】如图,AB=AC,AD=AE,点B、D、E在一条直线上,∠BAC=∠DAE,∠1=35.5°,∠2=30.5°,则∠3= 度.
答案 66
解析 如图所示:
∵∠BAC=∠DAE,∠BAC=∠1+∠DAC,∠DAE=∠DAC+∠4,
∴∠1=∠4,
在△ABD和△ACE中,,∴△ABD≌△ACE(SAS),
∴∠ADB=∠AEC,
又∵∠2+∠4+∠AEC=180°,∴∠AEC=114°,∴∠ADB=114°,
又∠ADB+∠3=180°,∴∠3=66°,
故答案为:66.
【例2-3】 在四边形ABCD中,E为BC边中点.已知:如图,若AE平分∠BAD,∠AED=90°,点F为AD上一点,AF=AB.
求证:(1)△ABE≌△AFE;(2)AD=AB+CD.
解析 (1)证明:∵AE平分∠BAD,∴∠BAE=∠FAE,
在△ABE和△AFE中,,
∴△ABE≌△AFE(SAS);
(2)证明:由(1)知,△ABE≌△AFE,
∴EB=EF,∠AEB=∠AEF,
∵∠BEC=180°,∠AED=90°,
∴∠AEB+∠DEC=90°,∠AEF+∠DEF=90°,
∴∠DEC=∠DEF,
∵点E为BC的中点,∴EB=EC,
∴EF=EC,
在△ECD和△EFD中,,∴△ECD≌△EFD(SAS),
∴DC=DF,
∵AD=AF+DF,AB=AF,
∴AD=AB+CD.
知识点3 综合利用SSS、SAS进行复杂的几何推理.
【例3-1】如图,点A,B,C,D在同一条直线上,,,.
求证:;
若,求三角形的面积.
【答案】(1) 见分析; (2)
【分析】(1)根据得,根据得,即,根据 即可证明;
(2)在中,以为底作为高,则,,根据 得,,即可得.
(1)证明:∵,
,
∵,
,
在和中,
,
;
(2)解:如图所示,在中,以为底作为高,
,,
∵,
,,
.
【点拨】本题考查了三角形的判定与性质,三角形的面积,解题的关键是理解题意,掌握这些知识点.
【例3-2】已知四边形中,,,如图2,点P,Q分别在线段,上,满足,求证:.
证明见分析
【分析】在的延长线上取点K,使得,连接,根据四边形内角和,证明,得到,,再证明,得到,进而推出,然后结合,即可证明结论.
解:证明:如图,在的延长线上取点K,使得,连接,
,
,
,
,
在和中,
,
,
,,
,
,
在和中,
,
,
,
,
,
,
,
,
,
.
【点拨】本题考查了全等三角形的判定和性质,四边形内角和,做辅助线构造全等三角形是解题关键.
【例3-3】已知:在和中,.
(1)如图①,若,求证:.
(2)如图②,若,则与间的等量关系式为__________,的大小为__________(直接写出结果,不证明)
【答案】(1)证明见解析
(2),α
【分析】(1)利用证明,即可得到结论;
(2)与(1)同理可证,得到,由得到,根据对顶角相等和三角形内角和定理得到即可.
【详解】(1)证明:∵,
∴,
∴.
在和中,,
∴,
∴;
(2)∵,
∴,
∴.
在和中,,
∴,
∴;
如图②,设与相交于点E,
∵,
∴,
在和中,
,,,
∴,
故答案为:,
【点评】此题考查了全等三角形的判定和性质、三角形内角和定理等知识,熟练掌握全等三角形的判定和性质是解题的关键.
能力强化提升训练
1 .如图,在中,,,平分,于E,若,则为 .
【答案】6
【分析】延长,交于点,证,,得出,,及,则,可以求出其值.
【详解】解:延长,交于点,
∵,
,,
∵,
,
在和中,
,
,
,
平分,
,
,
在和中,
,
,
,
,
,
,
,
故答案为:6.
【点评】本题考查了全等三角形的判定和性质,角平分线的定义,熟练掌握全等三角形的性质及判定是解题的关键.
如图,在中,,分别是,边上的高,在上取一点D,使,在射线上取一点G,使,连结,.若,,则的度数为 .
【答案】32度/
【分析】证明得到,根据三角形的内角和定理求得即可.
【详解】解:,分别是,边上的高,
.
,.
.
在和中,,,,
.
.
,
.
【点睛】本题考查三角形的高、全等三角形得判定与性质、三角形的内角和定理,证明是解答的关键.
如图,在中,,.过点作,垂足为,延长至点.使.在边上截取,连接.求证:.
【答案】见解析
【分析】利用三角形内角和定理得的度数,再根据全等三角形的判定与性质可得结论.
【详解】证明:在 中,,,
.
.
.
,
.
在和中,
,
∴.
.
【点评】此题考查的是全等三角形的判定与性质,掌握其性质定理是解决此题的关键.
4 .如图,在中,,分别是,边上的高,在上载取,延长至点使,连接,.
(1)求证:;
(2)求的度数;
【答案】(1)证明见解析
(2)
【分析】(1)根据高的定义得到,进而得到,由此证明即可证明;
(2)由全等三角形的性质得到,再由三角形内角和定理得到,即可得到,即.
【详解】(1)证明:、分别是、两条边上的高,
,
,
,
在与中,
,
,
;
(2)解:∵,
∴,
∵是边上的高,即,
∴,
∴,
∴,即.
【点评】本题考查了全等三角形的判定和性质,三角形内角和定理,高的定义,证明是解题的关键.
堂堂清
选择题(每小题4分,共32分)
1 .如图中全等的三角形是( )
A.①和② B.①和③ C.②和③ D.②和④
答案 B
解析 ①和③符合全等三角形的判定定理SAS,两三角形全等,而其它三角形不全等,
故选:B.
2 .如图,在2×3的正方形方格中,每个小正方形方格的边长都为1,则∠1和∠2的关系是( )
A.∠2=2∠1 B.∠2﹣∠1=90° C.∠1+∠2=180° D.∠1+∠2=90°
答案 D
解析 如图:
由题意得:AC=BD=2,BC=DE=1,∠ACB=∠BDE=90°,
∴∠1+∠BED=90°,
在△ABC和△BED中,,∴△ABC≌△BED(SAS),
∴∠2=∠BED,
∴∠1+∠2=90°,
故选:D.
3 .如图,有一池塘,要测量池塘两端A,B的距离时,可先在平地上取一个可以直接到达A和B的点C.连接AC并延长到D,使CD=CA.连接BC并延长到E,使CE=CB.可证明△EDC≌△BAC,从而得到ED=AB,则测得ED的长就是两点A,B的距离.判定△EDC≌△BAC的依据是( )
A.“边边边” B.“角边角” C.“角角边” D.“边角边”
答案 D
解析 由题意知AC=DC,BC=EC,且∠ACB=∠DCE(对顶角相等),
∴△ABC≌△DEC(SAS),∴DE=AB,
故选:D.
4 .如图,小明把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是( )
A.带①去 B.带②去 C.带③去 D.①②③都带去
【答案】A
【分析】根据全等三角形的判定可进行求解
【详解】解:第①块不仅保留了原来三角形的两个角还保留了一边,则可以根据来配一块一样的玻璃.
故选:A.
5 .如图,是和的公共边,下列条件不能判定的是( )
A., B.,
C., D.,
【答案】B
【分析】由全等三角形的判定方法:,,,即可判断.
【详解】解A、由可以判定,故不符合题意;
B、,这两个角分别是,的对角,不能判定,故符合题意;
C、由可以判定,故不符合题意;
D、由可以判定,故不符合题意.
故选:B.
【点评】本题考查全等三角形的判定,关键是掌握全等三角形的判定方法.
6 .如图,已知,,,,,则的度数为( )
A. B. C. D.
【答案】C
【分析】先证出,根据三角形全等的性质可得,再根据三角形的外角性质即可得.
【详解】解:,
,即,
在和中,,
,
,
,
,
故选:C.
【点评】本题考查了三角形全等的判定与性质、三角形的外角性质,熟练掌握三角形全等的判定与性质是解题关键.
7 .如图,把长短确定的两根木棍AB、AC的一端固定在A处,和第三根木棍BM摆出△ABC,木棍AB固定,木棍AC绕A转动,得到△ABD,这个实验说明( )
A.△ABC与△ABD不全等
B.有两边分别相等的两个三角形不一定全等
C.两边和它们的夹角分别相等的两个三角形全等
D.有两边和其中一边的对角分别相等的两个三角形不一定全等
【答案】D
【分析】根据全等三角形的判定方法即可判断;
【详解】由题意可知:AB=AB,AC=AD,∠ABC=∠ABD,
满足有两边和其中一边的对角分别相等,但是△ABC与△ABD不全等,
故选:D.
【点评】本题考查全等三角形的判定,记住有两边和其中一边的对角分别相等的两个三角形不一定全等.
8 .如图,在正方形方格中,每个小正方形的边长都是一个单位长度,点均在小正方形方格的顶点上,线段交于点,若,则等于( )
A. B. C. D.
【答案】C
【分析】根据三角形外角的性质及平行线的性质可进行求解.
解:如图,
由图可知:,,
∴,
∴,
∵,
∴,
∵,
∴,
∴;
故选C.
【点拨】本题主要考查全等三角形的性质与判定,熟练掌握全等三角形的性质与判定是解题的关键.
二、填空题(每小题4分,共20分)
9 .如图,已知AB∥CF,点E为DF的中点,若AB=9 cm,CF=5 cm,则BD=____cm.
【答案】4
【解析】解:∵AB∥CF,
∴∠A=∠ACF,∠AED=∠CEF,
在△AED和△CEF中
,
∴△AED≌△CEF(AAS),
∴FC=AD=5cm,
∴BD=AB-AD=9-5=4(cm).
故答案为:4
10 如图,在中,,,,分别在,,上,且,,,则的度数是_____.(用含的代数式表示)
【详解】解:∵AB=AC,
∴∠B=∠C,
在△BDF和△CED中,
,
∴△BDF≌△CED(SAS)
∴∠EDC=∠DFB
,
∴∠EDF=∠B=(180° ∠A)÷2=90° ∠A,
∵∠FDE=α,
∴∠A=180° 2α,
故答案为:180° 2α.
11 .如图,在中,,,是边上的中线,则的取值范围是________
【答案】2<AD<7
【分析】延长AD至点E,使得DE=AD,可证△ABD≌△CDE,可得AB=CE,AD=DE,在△ACE中,根据三角形三边关系即可求得AE的取值范围,从而得到的取值范围.
【详解】如图,延长AD至点E,使得DE=AD,
∵是边上的中线,
∴,
在△ABD和△CDE中,
,
∴△ABD△CDE(SAS),
∴AB=CE=5,AD=DE,
∵△ACE中,AC-CE<AE<AC+CE,
∴4<AE<14,
∴2<AD<7.
12 .如图,△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,D,E在同一条直线上,若∠CAE+∠ACE+∠ADE=130°,则∠ADE的度数为________°.
【答案】65
【分析】根据手拉手模型证明△ABD≌△ACE,可得∠ABD=∠ACE,再利用三角形外角的性质得∠ADE=∠BAD+∠ABD,再结合已知条件即可解答.
【详解】解:∵∠BAC=∠DAE,
∴∠BAC ∠DAC=∠DAE ∠DAC,
∴∠BAD=∠CAE,
∵AB=AC,AD=AE,
∴在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴∠ABD=∠ACE,
∵∠CAE+∠ACE+∠ADE=130°,
∴∠ABD+∠BAD+∠ADE=130°,
∵∠ADE=∠ABD+∠BAD,
∴2∠ADE=130°,
∴∠ADE=65°.
故答案为:65.
13 .如图,在△ABC中,AB=6,BC=5,AC=4,AD平分∠BAC交BC于点D,在AB上截取AE=AC,则△BDE的周长为____________
【答案】7
【分析】利用已知条件证明△ADE≌△ADC(SAS),得到ED=CD,从而BC=BD+CD=DE+BD=5,即可求得△BDE的周长.
【解答】解:∵AD是∠BAC的平分线,∴∠EAD=∠CAD
在△ADE和△ADC中,,∴△ADE≌△ADC(SAS),
∴ED=CD,∴BC=BD+CD=DE+BD=5,
∴△BDE的周长=BE+BD+ED=(6﹣4)+5=7.
【点评】本题考查了全等三角形的性质与判定,解决本题的关键是证明△ADE≌△ADC.
三、解答题(共6小题,48分)
14 .(8分)如图,.求证:.
【答案】见解析
【分析】由全等三角形的判定定理即可求证.
【详解】证明:∵,
∴
∵,
∴,
在和中,
.
∴.
【点评】本题考查利用“”证明三角形全等.掌握相关定理进行推导是解题关键.
15 .(8分)如图,在中,,.过点作,垂足为,延长至点.使.在边上截取,连接.求证:.
【答案】见解析
【分析】利用三角形内角和定理得的度数,再根据全等三角形的判定与性质可得结论.
【详解】证明:在 中,,,
.
.
.
,
.
在和中,
,
∴.
.
【点评】此题考查的是全等三角形的判定与性质,掌握其性质定理是解决此题的关键.
16 .(8分)如图,在和中,,,,连接,C、D、E三点在同一条直线上,连接.
(1)求证:;
(2)判断与的位置关系并说明理由.
【答案】(1)见解析
(2),见解析
【分析】(1)由“”可证,可得结论;
(2)由全等三角形的性质可得,由三角形内角和定理可求解.
【详解】(1)证明:∵,
∴,即,
在和中,,
∴,
∴;
(2)解:,理由如下:
如图,设与于G,
∵,
∴,
∵,,
∴,
∴.
【点评】本题考查了全等三角形的判定和性质,等腰直角三角形的性质,掌握全等三角形的判定是本题的关键.
17 .(8分).如图,在△ABC和△AEF中,AB=AC,AE=AF,∠BAC=∠EAF,BE与CF交于点O,与AC交于点D.
(1)求证:BE=CF;
(2)若∠BAC=80°,求∠BOF的度数.
答案 (1)略 (2) 100°
解析 (1)证明:∵∠CAB=∠EAF,∴∠CAB+∠CAE=∠EAF+∠CAE,
∴∠BAE=∠CAF,
在△BAE和△CAF中,,∴△BAE≌△CAF(SAS),
∴BE=CF;
(2)解:∵△BAE≌△CAF,∴∠EBA=∠FCA,即∠DBA=∠OCD,
∵∠BDA=∠ODC,∴∠BAD=∠COD,
∵∠BAC=80°,∴∠COD=80°,
∴∠BOF=100°.
18 .(8分)如图,在梯形ABCD中,AD∥BC,AE平分∠BAD,BE平分∠ABC,且AE、BE交CD于点E.试说明AD=AB﹣BC的理由.
【答案】见解析
【分析】在AB上找到F使得AF=AD,易证△AEF≌△AED,可得AF=AD,∠AFE=∠D,根据平行线性质可证∠C=∠BFE,即可证明△BEC≌△BEF,可得BF=BC,即可解题.
【详解】证明:在AB上找到F使得AF=AD,
∵AE平分∠BAD,
∴∠EAD=∠EAF,
∵在△AEF和△AED中,
,
∴△AEF≌△AED,(SAS)
∴AF=AD,∠AFE=∠D,
∵AD∥BC,
∴∠D+∠C=180°,
∵∠AFE+∠BFE=180°
∴∠C=∠BFE,
∵BE平分∠BAD,
∴∠FBE=∠C,
∵在△BEC和△BEF中,
,
∴△BEC≌△BEF,(AAS)
∴BF=BC,
∵AB=AF+BF,
∴AB=AD+BC,
即AD=AB﹣BC.
【点评】本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△AEF≌△AED和△BEC≌△BEF是解题的关键.
19 .(8分)如图,在四边形中,于,,.求证:(1);(2).
【答案】详见解析
【分析】过点向OA、OB作垂线,构建全等三角形,继而根据平角定义以及线段的和差即可证得结论.
【详解】如图,过点作与点,则∠F=∠CEO=90°,
,OC=OC,
,
,,
,,
,
,,
∵,,
.
【点睛】本题考查了全等三角形的判定与性质,正确添加辅助线构建全等三角形是解题的关键.
拓展培优*冲刺满分
如图,已知长方形ABCD的边长,,点E在边AB上,,如果点P从点B出发在线段BC上向点C运动,同时,点Q在线段DC上从点D向点C运动,已知点P的运动速度是2cm/s,则经过______s,与全等.
【答案】1或4
【分析】分两种情况:①当时,,②当时,,进而求出即可.
【详解】解:设运动的为s,分两种情况:
①当,时,,
∵,,
∴,
∴,
∵,
∴,
∴,
∵点P从点B出发在线段上以的速度向点C运动,
∴(s),此时点Q的运动速度为(cm/s);
②当,时,,
由题意得:,
解得:(s),此时点Q的运动速度为(cm/s);
综上,点P经过1或4s时;与全等.
故答案为:1或4.
【点评】此题主要考查了全等三角形的判定和性质等知识,关键是掌握两个三角形全等的判定和性质.
2 .问题发现:如图1,已知为线段上一点,分别以线段,为直角边作等腰直角三角形,,,,连接,,线段,之间的数量关系为______;位置关系为_______.
拓展探究:如图2,把绕点逆时针旋转,线段,交于点,则与之间的关系是否仍然成立?请说明理由.
【答案】问题发现:,;拓展探究:成立,理由见解析
【分析】问题发现:根据题目条件证△ACE≌△DCB,再根据全等三角形的性质即可得出答案;
拓展探究:用SAS证,根据全等三角形的性质即可证得.
【详解】解:问题发现:延长BD,交AE于点F,如图所示:
∵,
∴,
又∵,
∴(SAS),
,
∵,
∴,
∴,
∴,
,
故答案为:,;
拓展探究:成立.
理由如下:设与相交于点,如图1所示:
∵,
∴,
又∵,,
∴(SAS),
∴,,
∵,
∴,
∴,
∴,
即,依然成立.
【点评】本题考查全等三角形的判定和性质,三角形三边关系,手拉手模型,熟练掌握全等三角形的判定和手拉手模型是解决本题的关键.
3 .(1)阅读理解:如图1,在中,若,.求边上的中线的取值范围.解决此问题可以用如下方法:延长到点,使,再连接(或将绕着点逆时针旋转得到),把,,集中在中,利用三角形三边的关系即可判断中线的取值范围是______;
(2)问题解决:如图2,在中,是边上的中点,于点,交于点,交于点,连接,求证:;
(3)问题拓展:如图3,在四边形中,,,,以为顶点作一个角,角的两边分别交,于,两点,连接,探索线段,,之间的数量关系,并加以证明.
【答案】(1);(2)见解析;(3),证明见解析
【分析】(1)延长至,使,连接,证明,根据三角形三边关系即可求解;
(2)延长至点,使,连接,,同(1)得,,证明在中,由三角形的三边关系得,即可得证;
(3)延长至点,使,连接,证明,,根据求的三角形的性质即可得证.
【详解】(1)解:延长至,使,连接,如图①所示:
∵是边上的中线,
∴,
在和中,
∴,
∴,
在中,由三角形的三边关系得:,
∴,即,
∴;
故答案为:;
(2)证明:延长至点,使,连接,,如图所示
同(1)得,,
,,
,
在中,由三角形的三边关系得,
(3)
证明如下:
延长至点,使,连接,如图所示
,
在和中,
,
,
,
,
在和中,
,
.
,
【点睛】本题考查全等三角形的判定及性质、三角形三边关系、角的和差等,解答此题的关键是作出辅助线,构造出与图①中结构相关的图形.
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
八年级数学上分层优化堂堂清
十二章 全等三角形
12.2三角形全等的判定第二课时
学习目标:
1.能够利用尺规正确的画出一个与给定三角形满足SAS条件的全等的三角形,能准确叙述SAS.
2.能够利用SAS进行简单的几何推理(计算或证明)
3.能够利用SAS进行较复杂的几何推理(计算或证明)
4.能画图说明满足SSA条件的两个三角形不一定全等.能够综合利用SSS、SAS进行复杂的几何推理.
老师对你说:
知识点1 全等三角形的判定2:边角边(SAS)
三角形全等的判定2:边角边(SAS)
文字:在两个三角形中,如果有两条边及它们的夹角对应相等,那么这两个三角形全等;
图形:
符号:在与中,.
知识点2 利用SAS进行推理证明
①用“SAS”判定两个三角形全等时,必须满足“两边及它们的夹角”这一条件,在书写时,一般按“边角边”的顺序.
②有两边和其中一角对应相等的两个三角形不一定全等
知识点3 综合利用SSS、SAS进行复杂的几何推理.
证明三角形全等的“两个条件”(1)直接条件:已知中直接给出的边(角)对应相等,
隐含条件:已知中没有给出,但通过读图得到的条件,如公共边、公共角、对顶角。
“SAS”判定方法证明两个三角形全等及进行简单的应用.
1.证明线段相等或者角相等时,常常通过证明它们是全等三角形的对应边或对应角来解决.
2判断三角形全等时,注意两边与其中一边的对角相等的两个三角形不一定全等.解题时要根据已知条件的位置来考虑,只具备SSA时是不能判定三角形全等的.
基础提升 教材核心知识点精练
知识点1 全等三角形的判定2:边角边(SAS)
【例1-1】如图,AD⊥AB,AE⊥AC,AD=AB,AE=AC,则判定△ADC≌△ABE的根据是____.
【例1-2】如图,工人师傅设计了一种测零件内径的卡钳,卡钳交叉点O为、的中点,只要量出的长度,就可以道该零件内径的长度.依据的数学基本事实是( )
A.两边及其夹角分别相等的两个三角形全等 B.两角及其夹边分别相等的两个三角形全等
C.两余直线被一组平行线所截,所的对应线段成比例 D.两点之间线段最短
【例1-3】如图,与相交于点O,,不添加辅助线,判定的依据是( )
A. B. C. D.
知识点2 利用SAS进行推理证明
【例2-1】如图,在2×3的正方形方格中,每个小正方形方格的边长都为1,则∠1和∠2的关系是( )
A.∠2=2∠1 B.∠2﹣∠1=90° C.∠1+∠2=180° D.∠1+∠2=90°
【例2-2】如图,AB=AC,AD=AE,点B、D、E在一条直线上,∠BAC=∠DAE,∠1=35.5°,∠2=30.5°,则∠3= 度.
【例2-3】 在四边形ABCD中,E为BC边中点.已知:如图,若AE平分∠BAD,∠AED=90°,点F为AD上一点,AF=AB.
求证:(1)△ABE≌△AFE;(2)AD=AB+CD.
知识点3 综合利用SSS、SAS进行复杂的几何推理.
【例3-1】如图,点A,B,C,D在同一条直线上,,,.
求证:;
若,求三角形的面积.
【例3-2】已知四边形中,,,如图2,点P,Q分别在线段,上,满足,求证:.
【例3-3】已知:在和中,.
(1)如图①,若,求证:.
(2)如图②,若,则与间的等量关系式为__________,的大小为__________(直接写出结果,不证明)
能力强化提升训练
1 .如图,在中,,,平分,于E,若,则为 .
如图,在中,,分别是,边上的高,在上取一点D,使,在射线上取一点G,使,连结,.若,,则的度数为 .
如图,在中,,.过点作,垂足为,延长至点.使.在边上截取,连接.求证:.
4 .如图,在中,,分别是,边上的高,在上载取,延长至点使,连接,.
(1)求证:;
(2)求的度数;
堂堂清
选择题(每小题4分,共32分)
1 .如图中全等的三角形是( )
A.①和② B.①和③ C.②和③ D.②和④
2 .如图,在2×3的正方形方格中,每个小正方形方格的边长都为1,则∠1和∠2的关系是( )
A.∠2=2∠1 B.∠2﹣∠1=90° C.∠1+∠2=180° D.∠1+∠2=90°
3 .如图,有一池塘,要测量池塘两端A,B的距离时,可先在平地上取一个可以直接到达A和B的点C.连接AC并延长到D,使CD=CA.连接BC并延长到E,使CE=CB.可证明△EDC≌△BAC,从而得到ED=AB,则测得ED的长就是两点A,B的距离.判定△EDC≌△BAC的依据是( )
A.“边边边” B.“角边角” C.“角角边” D.“边角边”
4 .如图,小明把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是( )
A.带①去 B.带②去 C.带③去 D.①②③都带去
5 .如图,是和的公共边,下列条件不能判定的是( )
A., B.,
C., D.,
6 .如图,已知,,,,,则的度数为( )
A. B. C. D.
7 .如图,把长短确定的两根木棍AB、AC的一端固定在A处,和第三根木棍BM摆出△ABC,木棍AB固定,木棍AC绕A转动,得到△ABD,这个实验说明( )
A.△ABC与△ABD不全等
B.有两边分别相等的两个三角形不一定全等
C.两边和它们的夹角分别相等的两个三角形全等
D.有两边和其中一边的对角分别相等的两个三角形不一定全等
8 .如图,在正方形方格中,每个小正方形的边长都是一个单位长度,点均在小正方形方格的顶点上,线段交于点,若,则等于( )
A. B. C. D.
二、填空题(每小题4分,共20分)
9 .如图,已知AB∥CF,点E为DF的中点,若AB=9 cm,CF=5 cm,则BD=____cm.
10 如图,在中,,,,分别在,,上,且,,,则的度数是_____.(用含的代数式表示)
11 .如图,在中,,,是边上的中线,则的取值范围是________
12 .如图,△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,D,E在同一条直线上,若∠CAE+∠ACE+∠ADE=130°,则∠ADE的度数为________°.
13 .如图,在△ABC中,AB=6,BC=5,AC=4,AD平分∠BAC交BC于点D,在AB上截取AE=AC,则△BDE的周长为____________
三、解答题(共6小题,48分)
14 .(8分)如图,.求证:.
15 .(8分)如图,在中,,.过点作,垂足为,延长至点.使.在边上截取,连接.求证:.
16 .(8分)如图,在和中,,,,连接,C、D、E三点在同一条直线上,连接.
(1)求证:;
(2)判断与的位置关系并说明理由.
17 .(8分).如图,在△ABC和△AEF中,AB=AC,AE=AF,∠BAC=∠EAF,BE与CF交于点O,与AC交于点D.
(1)求证:BE=CF;
(2)若∠BAC=80°,求∠BOF的度数.
18 .(8分)如图,在梯形ABCD中,AD∥BC,AE平分∠BAD,BE平分∠ABC,且AE、BE交CD于点E.试说明AD=AB﹣BC的理由.
19 .(8分)如图,在四边形中,于,,.求证:(1);(2).
拓展培优*冲刺满分
如图,已知长方形ABCD的边长,,点E在边AB上,,如果点P从点B出发在线段BC上向点C运动,同时,点Q在线段DC上从点D向点C运动,已知点P的运动速度是2cm/s,则经过______s,与全等.
2 .问题发现:如图1,已知为线段上一点,分别以线段,为直角边作等腰直角三角形,,,,连接,,线段,之间的数量关系为______;位置关系为_______.
拓展探究:如图2,把绕点逆时针旋转,线段,交于点,则与之间的关系是否仍然成立?请说明理由.
3 .(1)阅读理解:如图1,在中,若,.求边上的中线的取值范围.解决此问题可以用如下方法:延长到点,使,再连接(或将绕着点逆时针旋转得到),把,,集中在中,利用三角形三边的关系即可判断中线的取值范围是______;
(2)问题解决:如图2,在中,是边上的中点,于点,交于点,交于点,连接,求证:;
(3)问题拓展:如图3,在四边形中,,,,以为顶点作一个角,角的两边分别交,于,两点,连接,探索线段,,之间的数量关系,并加以证明.
八年级数学上分层优化堂堂清
十二章 全等三角形
12.2三角形全等的判定第二课时(解析版)
学习目标:
1.能够利用尺规正确的画出一个与给定三角形满足SAS条件的全等的三角形,能准确叙述SAS.
2.能够利用SAS进行简单的几何推理(计算或证明)
3.能够利用SAS进行较复杂的几何推理(计算或证明)
4.能画图说明满足SSA条件的两个三角形不一定全等.能够综合利用SSS、SAS进行复杂的几何推理.
老师对你说:
知识点1 全等三角形的判定2:边角边(SAS)
三角形全等的判定2:边角边(SAS)
文字:在两个三角形中,如果有两条边及它们的夹角对应相等,那么这两个三角形全等;
图形:
符号:在与中,.
知识点2 利用SAS进行推理证明
①用“SAS”判定两个三角形全等时,必须满足“两边及它们的夹角”这一条件,在书写时,一般按“边角边”的顺序.
②有两边和其中一角对应相等的两个三角形不一定全等
知识点3 综合利用SSS、SAS进行复杂的几何推理.
证明三角形全等的“两个条件”(1)直接条件:已知中直接给出的边(角)对应相等,
隐含条件:已知中没有给出,但通过读图得到的条件,如公共边、公共角、对顶角。
“SAS”判定方法证明两个三角形全等及进行简单的应用.
1.证明线段相等或者角相等时,常常通过证明它们是全等三角形的对应边或对应角来解决.
2判断三角形全等时,注意两边与其中一边的对角相等的两个三角形不一定全等.解题时要根据已知条件的位置来考虑,只具备SSA时是不能判定三角形全等的.
基础提升 教材核心知识点精练
知识点1 全等三角形的判定2:边角边(SAS)
【例1-1】如图,AD⊥AB,AE⊥AC,AD=AB,AE=AC,则判定△ADC≌△ABE的根据是____.
【答案】SAS
【解析】∵AD⊥AB,AE⊥AC,∴∠DAB=∠EAC=90°,∴∠DAB+∠BAC=∠EAC+∠BAC,即:∠DAC=∠BAE,
在△ADC和△ABE中,AD=AB,∠DAC=∠BAE,AE=AC,
∴△ADC≌△ABE(SAS),故填:SAS.
【点评】本题考查全等三角形的判定和性质、三角形的外角的性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型
【例1-2】如图,工人师傅设计了一种测零件内径的卡钳,卡钳交叉点O为、的中点,只要量出的长度,就可以道该零件内径的长度.依据的数学基本事实是( )
A.两边及其夹角分别相等的两个三角形全等 B.两角及其夹边分别相等的两个三角形全等
C.两余直线被一组平行线所截,所的对应线段成比例 D.两点之间线段最短
【答案】A
【分析】根据题意易证,根据证明方法即可求解.
解:O为、的中点,
,,
(对顶角相等),
在与中,
,
,
,
故选:A.
【点拨】本题考查了全等三角形的证明,正确使用全等三角形的证明方法是解题的关键.
【例1-3】如图,与相交于点O,,不添加辅助线,判定的依据是( )
A. B. C. D.
【答案】B
【分析】根据,,正好是两边一夹角,即可得出答案.
解:∵在△ABO和△DCO中,,
∴,故B正确.
故选:B.
【点拨】本题主要考查了全等三角形的判定,熟练掌握两边对应相等,且其夹角也对应相等的两个三角形全等,是解题的关键.
知识点2 利用SAS进行推理证明
【例2-1】如图,在2×3的正方形方格中,每个小正方形方格的边长都为1,则∠1和∠2的关系是( )
A.∠2=2∠1 B.∠2﹣∠1=90° C.∠1+∠2=180° D.∠1+∠2=90°
答案 D
解析 如图:
由题意得:AC=BD=2,BC=DE=1,∠ACB=∠BDE=90°,
∴∠1+∠BED=90°,
在△ABC和△BED中,,∴△ABC≌△BED(SAS),
∴∠2=∠BED,
∴∠1+∠2=90°,
故选:D.
【例2-2】如图,AB=AC,AD=AE,点B、D、E在一条直线上,∠BAC=∠DAE,∠1=35.5°,∠2=30.5°,则∠3= 度.
答案 66
解析 如图所示:
∵∠BAC=∠DAE,∠BAC=∠1+∠DAC,∠DAE=∠DAC+∠4,
∴∠1=∠4,
在△ABD和△ACE中,,∴△ABD≌△ACE(SAS),
∴∠ADB=∠AEC,
又∵∠2+∠4+∠AEC=180°,∴∠AEC=114°,∴∠ADB=114°,
又∠ADB+∠3=180°,∴∠3=66°,
故答案为:66.
【例2-3】 在四边形ABCD中,E为BC边中点.已知:如图,若AE平分∠BAD,∠AED=90°,点F为AD上一点,AF=AB.
求证:(1)△ABE≌△AFE;(2)AD=AB+CD.
解析 (1)证明:∵AE平分∠BAD,∴∠BAE=∠FAE,
在△ABE和△AFE中,,
∴△ABE≌△AFE(SAS);
(2)证明:由(1)知,△ABE≌△AFE,
∴EB=EF,∠AEB=∠AEF,
∵∠BEC=180°,∠AED=90°,
∴∠AEB+∠DEC=90°,∠AEF+∠DEF=90°,
∴∠DEC=∠DEF,
∵点E为BC的中点,∴EB=EC,
∴EF=EC,
在△ECD和△EFD中,,∴△ECD≌△EFD(SAS),
∴DC=DF,
∵AD=AF+DF,AB=AF,
∴AD=AB+CD.
知识点3 综合利用SSS、SAS进行复杂的几何推理.
【例3-1】如图,点A,B,C,D在同一条直线上,,,.
求证:;
若,求三角形的面积.
【答案】(1) 见分析; (2)
【分析】(1)根据得,根据得,即,根据 即可证明;
(2)在中,以为底作为高,则,,根据 得,,即可得.
(1)证明:∵,
,
∵,
,
在和中,
,
;
(2)解:如图所示,在中,以为底作为高,
,,
∵,
,,
.
【点拨】本题考查了三角形的判定与性质,三角形的面积,解题的关键是理解题意,掌握这些知识点.
【例3-2】已知四边形中,,,如图2,点P,Q分别在线段,上,满足,求证:.
证明见分析
【分析】在的延长线上取点K,使得,连接,根据四边形内角和,证明,得到,,再证明,得到,进而推出,然后结合,即可证明结论.
解:证明:如图,在的延长线上取点K,使得,连接,
,
,
,
,
在和中,
,
,
,,
,
,
在和中,
,
,
,
,
,
,
,
,
,
.
【点拨】本题考查了全等三角形的判定和性质,四边形内角和,做辅助线构造全等三角形是解题关键.
【例3-3】已知:在和中,.
(1)如图①,若,求证:.
(2)如图②,若,则与间的等量关系式为__________,的大小为__________(直接写出结果,不证明)
【答案】(1)证明见解析
(2),α
【分析】(1)利用证明,即可得到结论;
(2)与(1)同理可证,得到,由得到,根据对顶角相等和三角形内角和定理得到即可.
【详解】(1)证明:∵,
∴,
∴.
在和中,,
∴,
∴;
(2)∵,
∴,
∴.
在和中,,
∴,
∴;
如图②,设与相交于点E,
∵,
∴,
在和中,
,,,
∴,
故答案为:,
【点评】此题考查了全等三角形的判定和性质、三角形内角和定理等知识,熟练掌握全等三角形的判定和性质是解题的关键.
能力强化提升训练
1 .如图,在中,,,平分,于E,若,则为 .
【答案】6
【分析】延长,交于点,证,,得出,,及,则,可以求出其值.
【详解】解:延长,交于点,
∵,
,,
∵,
,
在和中,
,
,
,
平分,
,
,
在和中,
,
,
,
,
,
,
,
故答案为:6.
【点评】本题考查了全等三角形的判定和性质,角平分线的定义,熟练掌握全等三角形的性质及判定是解题的关键.
如图,在中,,分别是,边上的高,在上取一点D,使,在射线上取一点G,使,连结,.若,,则的度数为 .
【答案】32度/
【分析】证明得到,根据三角形的内角和定理求得即可.
【详解】解:,分别是,边上的高,
.
,.
.
在和中,,,,
.
.
,
.
【点睛】本题考查三角形的高、全等三角形得判定与性质、三角形的内角和定理,证明是解答的关键.
如图,在中,,.过点作,垂足为,延长至点.使.在边上截取,连接.求证:.
【答案】见解析
【分析】利用三角形内角和定理得的度数,再根据全等三角形的判定与性质可得结论.
【详解】证明:在 中,,,
.
.
.
,
.
在和中,
,
∴.
.
【点评】此题考查的是全等三角形的判定与性质,掌握其性质定理是解决此题的关键.
4 .如图,在中,,分别是,边上的高,在上载取,延长至点使,连接,.
(1)求证:;
(2)求的度数;
【答案】(1)证明见解析
(2)
【分析】(1)根据高的定义得到,进而得到,由此证明即可证明;
(2)由全等三角形的性质得到,再由三角形内角和定理得到,即可得到,即.
【详解】(1)证明:、分别是、两条边上的高,
,
,
,
在与中,
,
,
;
(2)解:∵,
∴,
∵是边上的高,即,
∴,
∴,
∴,即.
【点评】本题考查了全等三角形的判定和性质,三角形内角和定理,高的定义,证明是解题的关键.
堂堂清
选择题(每小题4分,共32分)
1 .如图中全等的三角形是( )
A.①和② B.①和③ C.②和③ D.②和④
答案 B
解析 ①和③符合全等三角形的判定定理SAS,两三角形全等,而其它三角形不全等,
故选:B.
2 .如图,在2×3的正方形方格中,每个小正方形方格的边长都为1,则∠1和∠2的关系是( )
A.∠2=2∠1 B.∠2﹣∠1=90° C.∠1+∠2=180° D.∠1+∠2=90°
答案 D
解析 如图:
由题意得:AC=BD=2,BC=DE=1,∠ACB=∠BDE=90°,
∴∠1+∠BED=90°,
在△ABC和△BED中,,∴△ABC≌△BED(SAS),
∴∠2=∠BED,
∴∠1+∠2=90°,
故选:D.
3 .如图,有一池塘,要测量池塘两端A,B的距离时,可先在平地上取一个可以直接到达A和B的点C.连接AC并延长到D,使CD=CA.连接BC并延长到E,使CE=CB.可证明△EDC≌△BAC,从而得到ED=AB,则测得ED的长就是两点A,B的距离.判定△EDC≌△BAC的依据是( )
A.“边边边” B.“角边角” C.“角角边” D.“边角边”
答案 D
解析 由题意知AC=DC,BC=EC,且∠ACB=∠DCE(对顶角相等),
∴△ABC≌△DEC(SAS),∴DE=AB,
故选:D.
4 .如图,小明把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是( )
A.带①去 B.带②去 C.带③去 D.①②③都带去
【答案】A
【分析】根据全等三角形的判定可进行求解
【详解】解:第①块不仅保留了原来三角形的两个角还保留了一边,则可以根据来配一块一样的玻璃.
故选:A.
5 .如图,是和的公共边,下列条件不能判定的是( )
A., B.,
C., D.,
【答案】B
【分析】由全等三角形的判定方法:,,,即可判断.
【详解】解A、由可以判定,故不符合题意;
B、,这两个角分别是,的对角,不能判定,故符合题意;
C、由可以判定,故不符合题意;
D、由可以判定,故不符合题意.
故选:B.
【点评】本题考查全等三角形的判定,关键是掌握全等三角形的判定方法.
6 .如图,已知,,,,,则的度数为( )
A. B. C. D.
【答案】C
【分析】先证出,根据三角形全等的性质可得,再根据三角形的外角性质即可得.
【详解】解:,
,即,
在和中,,
,
,
,
,
故选:C.
【点评】本题考查了三角形全等的判定与性质、三角形的外角性质,熟练掌握三角形全等的判定与性质是解题关键.
7 .如图,把长短确定的两根木棍AB、AC的一端固定在A处,和第三根木棍BM摆出△ABC,木棍AB固定,木棍AC绕A转动,得到△ABD,这个实验说明( )
A.△ABC与△ABD不全等
B.有两边分别相等的两个三角形不一定全等
C.两边和它们的夹角分别相等的两个三角形全等
D.有两边和其中一边的对角分别相等的两个三角形不一定全等
【答案】D
【分析】根据全等三角形的判定方法即可判断;
【详解】由题意可知:AB=AB,AC=AD,∠ABC=∠ABD,
满足有两边和其中一边的对角分别相等,但是△ABC与△ABD不全等,
故选:D.
【点评】本题考查全等三角形的判定,记住有两边和其中一边的对角分别相等的两个三角形不一定全等.
8 .如图,在正方形方格中,每个小正方形的边长都是一个单位长度,点均在小正方形方格的顶点上,线段交于点,若,则等于( )
A. B. C. D.
【答案】C
【分析】根据三角形外角的性质及平行线的性质可进行求解.
解:如图,
由图可知:,,
∴,
∴,
∵,
∴,
∵,
∴,
∴;
故选C.
【点拨】本题主要考查全等三角形的性质与判定,熟练掌握全等三角形的性质与判定是解题的关键.
二、填空题(每小题4分,共20分)
9 .如图,已知AB∥CF,点E为DF的中点,若AB=9 cm,CF=5 cm,则BD=____cm.
【答案】4
【解析】解:∵AB∥CF,
∴∠A=∠ACF,∠AED=∠CEF,
在△AED和△CEF中
,
∴△AED≌△CEF(AAS),
∴FC=AD=5cm,
∴BD=AB-AD=9-5=4(cm).
故答案为:4
10 如图,在中,,,,分别在,,上,且,,,则的度数是_____.(用含的代数式表示)
【详解】解:∵AB=AC,
∴∠B=∠C,
在△BDF和△CED中,
,
∴△BDF≌△CED(SAS)
∴∠EDC=∠DFB
,
∴∠EDF=∠B=(180° ∠A)÷2=90° ∠A,
∵∠FDE=α,
∴∠A=180° 2α,
故答案为:180° 2α.
11 .如图,在中,,,是边上的中线,则的取值范围是________
【答案】2<AD<7
【分析】延长AD至点E,使得DE=AD,可证△ABD≌△CDE,可得AB=CE,AD=DE,在△ACE中,根据三角形三边关系即可求得AE的取值范围,从而得到的取值范围.
【详解】如图,延长AD至点E,使得DE=AD,
∵是边上的中线,
∴,
在△ABD和△CDE中,
,
∴△ABD△CDE(SAS),
∴AB=CE=5,AD=DE,
∵△ACE中,AC-CE<AE<AC+CE,
∴4<AE<14,
∴2<AD<7.
12 .如图,△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,D,E在同一条直线上,若∠CAE+∠ACE+∠ADE=130°,则∠ADE的度数为________°.
【答案】65
【分析】根据手拉手模型证明△ABD≌△ACE,可得∠ABD=∠ACE,再利用三角形外角的性质得∠ADE=∠BAD+∠ABD,再结合已知条件即可解答.
【详解】解:∵∠BAC=∠DAE,
∴∠BAC ∠DAC=∠DAE ∠DAC,
∴∠BAD=∠CAE,
∵AB=AC,AD=AE,
∴在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴∠ABD=∠ACE,
∵∠CAE+∠ACE+∠ADE=130°,
∴∠ABD+∠BAD+∠ADE=130°,
∵∠ADE=∠ABD+∠BAD,
∴2∠ADE=130°,
∴∠ADE=65°.
故答案为:65.
13 .如图,在△ABC中,AB=6,BC=5,AC=4,AD平分∠BAC交BC于点D,在AB上截取AE=AC,则△BDE的周长为____________
【答案】7
【分析】利用已知条件证明△ADE≌△ADC(SAS),得到ED=CD,从而BC=BD+CD=DE+BD=5,即可求得△BDE的周长.
【解答】解:∵AD是∠BAC的平分线,∴∠EAD=∠CAD
在△ADE和△ADC中,,∴△ADE≌△ADC(SAS),
∴ED=CD,∴BC=BD+CD=DE+BD=5,
∴△BDE的周长=BE+BD+ED=(6﹣4)+5=7.
【点评】本题考查了全等三角形的性质与判定,解决本题的关键是证明△ADE≌△ADC.
三、解答题(共6小题,48分)
14 .(8分)如图,.求证:.
【答案】见解析
【分析】由全等三角形的判定定理即可求证.
【详解】证明:∵,
∴
∵,
∴,
在和中,
.
∴.
【点评】本题考查利用“”证明三角形全等.掌握相关定理进行推导是解题关键.
15 .(8分)如图,在中,,.过点作,垂足为,延长至点.使.在边上截取,连接.求证:.
【答案】见解析
【分析】利用三角形内角和定理得的度数,再根据全等三角形的判定与性质可得结论.
【详解】证明:在 中,,,
.
.
.
,
.
在和中,
,
∴.
.
【点评】此题考查的是全等三角形的判定与性质,掌握其性质定理是解决此题的关键.
16 .(8分)如图,在和中,,,,连接,C、D、E三点在同一条直线上,连接.
(1)求证:;
(2)判断与的位置关系并说明理由.
【答案】(1)见解析
(2),见解析
【分析】(1)由“”可证,可得结论;
(2)由全等三角形的性质可得,由三角形内角和定理可求解.
【详解】(1)证明:∵,
∴,即,
在和中,,
∴,
∴;
(2)解:,理由如下:
如图,设与于G,
∵,
∴,
∵,,
∴,
∴.
【点评】本题考查了全等三角形的判定和性质,等腰直角三角形的性质,掌握全等三角形的判定是本题的关键.
17 .(8分).如图,在△ABC和△AEF中,AB=AC,AE=AF,∠BAC=∠EAF,BE与CF交于点O,与AC交于点D.
(1)求证:BE=CF;
(2)若∠BAC=80°,求∠BOF的度数.
答案 (1)略 (2) 100°
解析 (1)证明:∵∠CAB=∠EAF,∴∠CAB+∠CAE=∠EAF+∠CAE,
∴∠BAE=∠CAF,
在△BAE和△CAF中,,∴△BAE≌△CAF(SAS),
∴BE=CF;
(2)解:∵△BAE≌△CAF,∴∠EBA=∠FCA,即∠DBA=∠OCD,
∵∠BDA=∠ODC,∴∠BAD=∠COD,
∵∠BAC=80°,∴∠COD=80°,
∴∠BOF=100°.
18 .(8分)如图,在梯形ABCD中,AD∥BC,AE平分∠BAD,BE平分∠ABC,且AE、BE交CD于点E.试说明AD=AB﹣BC的理由.
【答案】见解析
【分析】在AB上找到F使得AF=AD,易证△AEF≌△AED,可得AF=AD,∠AFE=∠D,根据平行线性质可证∠C=∠BFE,即可证明△BEC≌△BEF,可得BF=BC,即可解题.
【详解】证明:在AB上找到F使得AF=AD,
∵AE平分∠BAD,
∴∠EAD=∠EAF,
∵在△AEF和△AED中,
,
∴△AEF≌△AED,(SAS)
∴AF=AD,∠AFE=∠D,
∵AD∥BC,
∴∠D+∠C=180°,
∵∠AFE+∠BFE=180°
∴∠C=∠BFE,
∵BE平分∠BAD,
∴∠FBE=∠C,
∵在△BEC和△BEF中,
,
∴△BEC≌△BEF,(AAS)
∴BF=BC,
∵AB=AF+BF,
∴AB=AD+BC,
即AD=AB﹣BC.
【点评】本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△AEF≌△AED和△BEC≌△BEF是解题的关键.
19 .(8分)如图,在四边形中,于,,.求证:(1);(2).
【答案】详见解析
【分析】过点向OA、OB作垂线,构建全等三角形,继而根据平角定义以及线段的和差即可证得结论.
【详解】如图,过点作与点,则∠F=∠CEO=90°,
,OC=OC,
,
,,
,,
,
,,
∵,,
.
【点睛】本题考查了全等三角形的判定与性质,正确添加辅助线构建全等三角形是解题的关键.
拓展培优*冲刺满分
如图,已知长方形ABCD的边长,,点E在边AB上,,如果点P从点B出发在线段BC上向点C运动,同时,点Q在线段DC上从点D向点C运动,已知点P的运动速度是2cm/s,则经过______s,与全等.
【答案】1或4
【分析】分两种情况:①当时,,②当时,,进而求出即可.
【详解】解:设运动的为s,分两种情况:
①当,时,,
∵,,
∴,
∴,
∵,
∴,
∴,
∵点P从点B出发在线段上以的速度向点C运动,
∴(s),此时点Q的运动速度为(cm/s);
②当,时,,
由题意得:,
解得:(s),此时点Q的运动速度为(cm/s);
综上,点P经过1或4s时;与全等.
故答案为:1或4.
【点评】此题主要考查了全等三角形的判定和性质等知识,关键是掌握两个三角形全等的判定和性质.
2 .问题发现:如图1,已知为线段上一点,分别以线段,为直角边作等腰直角三角形,,,,连接,,线段,之间的数量关系为______;位置关系为_______.
拓展探究:如图2,把绕点逆时针旋转,线段,交于点,则与之间的关系是否仍然成立?请说明理由.
【答案】问题发现:,;拓展探究:成立,理由见解析
【分析】问题发现:根据题目条件证△ACE≌△DCB,再根据全等三角形的性质即可得出答案;
拓展探究:用SAS证,根据全等三角形的性质即可证得.
【详解】解:问题发现:延长BD,交AE于点F,如图所示:
∵,
∴,
又∵,
∴(SAS),
,
∵,
∴,
∴,
∴,
,
故答案为:,;
拓展探究:成立.
理由如下:设与相交于点,如图1所示:
∵,
∴,
又∵,,
∴(SAS),
∴,,
∵,
∴,
∴,
∴,
即,依然成立.
【点评】本题考查全等三角形的判定和性质,三角形三边关系,手拉手模型,熟练掌握全等三角形的判定和手拉手模型是解决本题的关键.
3 .(1)阅读理解:如图1,在中,若,.求边上的中线的取值范围.解决此问题可以用如下方法:延长到点,使,再连接(或将绕着点逆时针旋转得到),把,,集中在中,利用三角形三边的关系即可判断中线的取值范围是______;
(2)问题解决:如图2,在中,是边上的中点,于点,交于点,交于点,连接,求证:;
(3)问题拓展:如图3,在四边形中,,,,以为顶点作一个角,角的两边分别交,于,两点,连接,探索线段,,之间的数量关系,并加以证明.
【答案】(1);(2)见解析;(3),证明见解析
【分析】(1)延长至,使,连接,证明,根据三角形三边关系即可求解;
(2)延长至点,使,连接,,同(1)得,,证明在中,由三角形的三边关系得,即可得证;
(3)延长至点,使,连接,证明,,根据求的三角形的性质即可得证.
【详解】(1)解:延长至,使,连接,如图①所示:
∵是边上的中线,
∴,
在和中,
∴,
∴,
在中,由三角形的三边关系得:,
∴,即,
∴;
故答案为:;
(2)证明:延长至点,使,连接,,如图所示
同(1)得,,
,,
,
在中,由三角形的三边关系得,
(3)
证明如下:
延长至点,使,连接,如图所示
,
在和中,
,
,
,
,
在和中,
,
.
,
【点睛】本题考查全等三角形的判定及性质、三角形三边关系、角的和差等,解答此题的关键是作出辅助线,构造出与图①中结构相关的图形.
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
