八年级数学上分层优化堂堂清(6)三角形全等的重要模型—倍长中线(含解析)
文档属性
| 名称 | 八年级数学上分层优化堂堂清(6)三角形全等的重要模型—倍长中线(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-20 16:04:24 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
八年级数学上分层优化堂堂清
十二章 全等三角形
12.2三角形全等的重要模型
倍长中线模型
学习目标:
了解倍长中线法的基本方法。
会运用倍长中线法构造全等三角形证明和计算;
3、提高推理能力,获得成功的体验,增强学习的自信心。
老师对你说:
全等三角形在中考数学几何模块中占据着重要地位,也是学生必须掌握的一块内容,本专题就全等三角形中的重要模型--倍长中线模型进行梳理及对应试题分析,方便掌握。
全等三角形的对应边相等,对应角相等是证线段相等或角相等的重要依据,在解题过程中若不能直接运用,则需要通过作辅助线来构造全等三角形,若已知条件中存在中线,可将中线延长,将要求解或证明的结论进行转化,进而解决问题。
倍长中线法定义
延长三角形的中线,使得延长后的线段是原中线的两倍.
其目的是构造一对对顶的全等三角形;其本质是转移边和角.
示例剖析
其中,延长使得,则.
其模型也属于“字型或成字型”.
基本模式:
1.基本型:如图1,在三角形ABC中,AD为BC边上的中线.
证明思路:延长AD至点E,使得AD=DE. 若连结BE,则;若连结EC,则;
2、中点型:如图2,为的中点.
证明思路:若延长至点,使得,连结,则;
若延长至点,使得,连结,则.
3、中点+平行线型:如图3, ,点为线段的中点.
证明思路:延长交于点 (或交延长线于点),则.
【例1-1】【阅读理解】
课外兴趣小组活动时,老师提出了如下问题:
如图,△ABC中,若AB=8,AC=6,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:如图,延长AD到点E,使DE=AD,连结BE.请根据小明的方法思考:
(1)由已知和作图能得到的理由是( ).
A.SSS B.SAS C.AAS D.ASA
(2)AD的取值范围是( ).
A. B. C. D.
(3)【感悟】解题时,条件中若出现“中点”、“中线”字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论转化到同一个三角形中.
【问题解决】如图,AD是△ABC的中线,BE交AC于点E,交AD于F,且AE=EF.求证:AC=BF.
【例1-2】【教材呈现】如图是华师版八年级上册数学教材第69页的部分内容:
如图,在中,D是边BC的中点,过点C画直线CE,使,交AD的延长线于点E,求证:
证明∵(已知)
∴,(两直线平行,内错角相等).
在与中,
∵,(已证),
(已知),
∴,
∴(全等三角形的对应边相等).
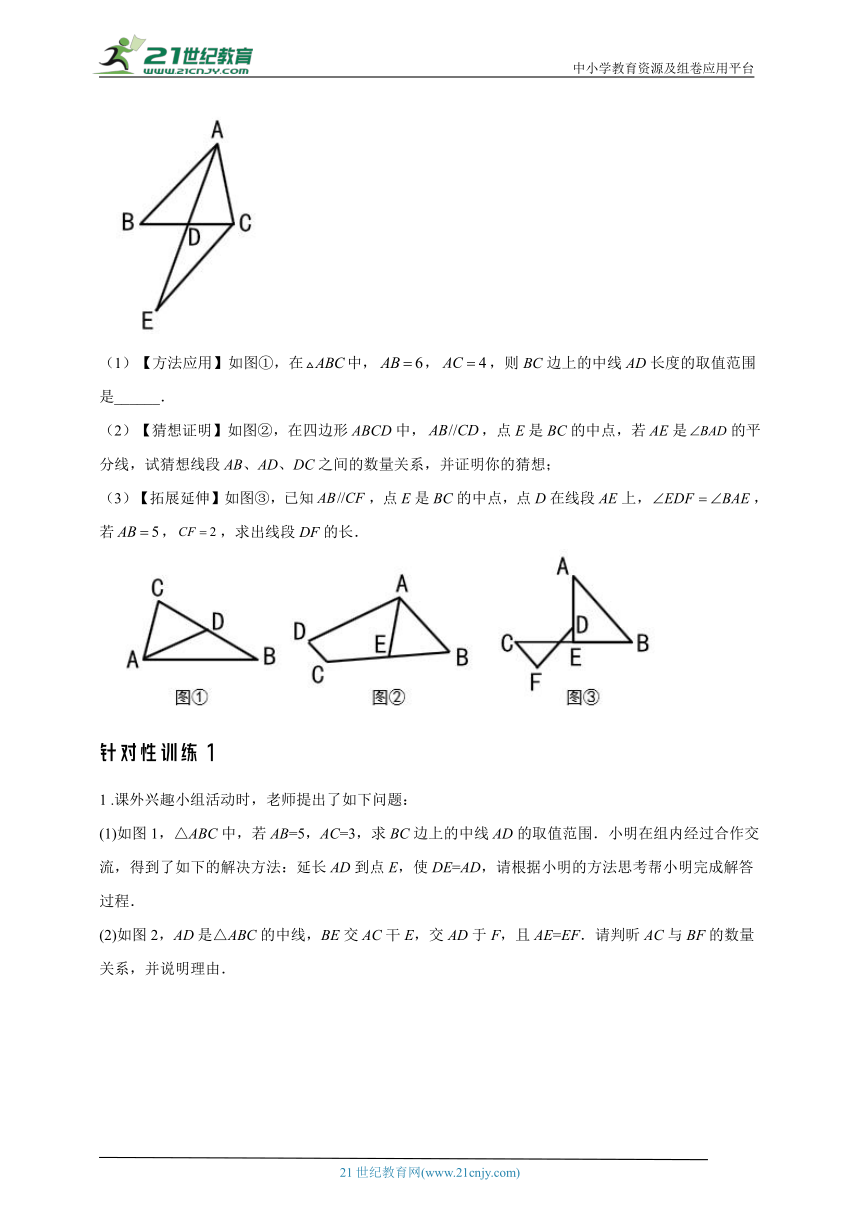
(1)【方法应用】如图①,在中,,,则BC边上的中线AD长度的取值范围是______.
(2)【猜想证明】如图②,在四边形ABCD中,,点E是BC的中点,若AE是的平分线,试猜想线段AB、AD、DC之间的数量关系,并证明你的猜想;
(3)【拓展延伸】如图③,已知,点E是BC的中点,点D在线段AE上,,若,,求出线段DF的长.
针对性训练1
1 .课外兴趣小组活动时,老师提出了如下问题:
(1)如图1,△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到点E,使DE=AD,请根据小明的方法思考帮小明完成解答过程.
(2)如图2,AD是△ABC的中线,BE交AC干E,交AD于F,且AE=EF.请判昕AC与BF的数量关系,并说明理由.
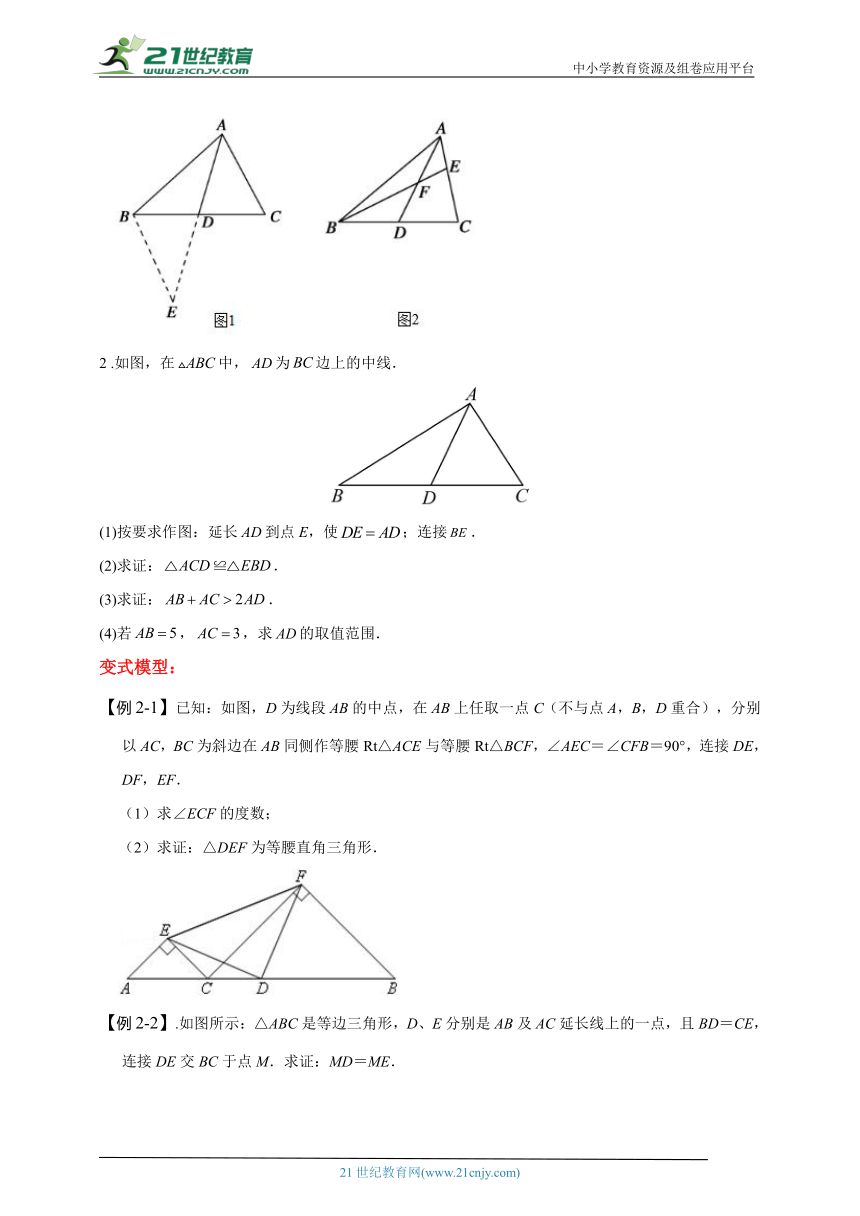
2 .如图,在中,为边上的中线.
(1)按要求作图:延长到点E,使;连接.
(2)求证:.
(3)求证:.
(4)若,,求的取值范围.
变式模型:
【例2-1】已知:如图,D为线段AB的中点,在AB上任取一点C(不与点A,B,D重合),分别以AC,BC为斜边在AB同侧作等腰Rt△ACE与等腰Rt△BCF,∠AEC=∠CFB=90°,连接DE,DF,EF.
(1)求∠ECF的度数;
(2)求证:△DEF为等腰直角三角形.
【例2-2】.如图所示:△ABC是等边三角形,D、E分别是AB及AC延长线上的一点,且BD=CE,连接DE交BC于点M.求证:MD=ME.
【例2-3】如图,在△ABC,AD平分∠BAC,E、F分别在BD、AD上,且DE=CD,EF=AC,求证:EF∥AB.
针对性训练2
1.如图,点P为等边△ABC的边AB上一点,Q为BC延长线上一点,AP=CQ,PQ交AC于D,
(1)求证:DP=DQ;
(2)过P作PE⊥AC于E,若BC=4,求DE的长.
2 .如图,分别以△ABC的边AB,AC为一边在三角形外作正方形ABEF和ACGH,M为FH上的中点,求证:MA⊥BC.
巩固提高
1.是的中线,,则的取值可能是( )
A.3 B.6 C.8 D.12
2.如图,在中,为中线,且,则边的取值范围是___________.
3.如图,中,为的中点,是上一点,连接并延长交于,,且,,那么的长度为__.
4.规定:有两组边相等,且它们所夹的角互补的两个三角形叫兄弟三角形.如图,,,,回答下列问题:
(1)求证:和是兄弟三角形.
(2)取的中点P,连接,请证明.
5 .已知:如图,△ABC和△DEF,,,AP、DQ分别是BC和EF边上的高,且.求证:;
(2)如果(1)中的条件不变,“如图”二字去掉,那么△ABC与△DEF全等吗 如果全等请证明,如果不全等请举出反例.
(3)如果把(1)中的条件“AP、DQ分别是BC和EF边上的高”改为“AP、DQ分别是BC和EF边上的中线”,请证明:.
6 .(1)已知如图1,在中,,求边上的中线的取值范围.
(2)思考:已知如图2,是的中线,,试探究线段与的数量和位置关系,并加以证明.
7.课堂上,老师出示了这样一个问题:
如图1,点D是△ABC边BC的中点,AB=5,AC=3,求AD的取值范围.
(1)小明的想法是,过点B作BE∥AC交AD的延长线于点E,如图2,从而通过构造全等解决问题,请你按照小明的想法解决此问题;
(2)请按照上述提示,解决下面问题:
在等腰Rt△ABC中,∠BAC=90°,AB=AC,点D是边AC延长线上一点,连接BD,过点A作AE⊥BD于点E,过点A作AF⊥AE,且AF=AE,连接EF交BC于点G,连接CF,求证BG=CG.
8.如图,△ABC中,BD=DC=AC,E是DC的中点,求证:AB=2AE.
八年级数学上分层优化堂堂清
十二章 全等三角形
12.2三角形全等的重要模型
倍长中线模型(解析版)
学习目标:
了解倍长中线法的基本方法。
会运用倍长中线法构造全等三角形证明和计算;
3、提高推理能力,获得成功的体验,增强学习的自信心。
老师对你说:
全等三角形在中考数学几何模块中占据着重要地位,也是学生必须掌握的一块内容,本专题就全等三角形中的重要模型--倍长中线模型进行梳理及对应试题分析,方便掌握。
全等三角形的对应边相等,对应角相等是证线段相等或角相等的重要依据,在解题过程中若不能直接运用,则需要通过作辅助线来构造全等三角形,若已知条件中存在中线,可将中线延长,将要求解或证明的结论进行转化,进而解决问题。
倍长中线法定义
延长三角形的中线,使得延长后的线段是原中线的两倍.
其目的是构造一对对顶的全等三角形;其本质是转移边和角.
示例剖析
其中,延长使得,则.
其模型也属于“字型或成字型”.
基本方法:
1.基本型:如图1,在三角形ABC中,AD为BC边上的中线.
证明思路:延长AD至点E,使得AD=DE. 若连结BE,则;若连结EC,则;
2、中点型:如图2,为的中点.
证明思路:若延长至点,使得,连结,则;
若延长至点,使得,连结,则.
3、中点+平行线型:如图3, ,点为线段的中点.
证明思路:延长交于点 (或交延长线于点),则.
【例1-1】【阅读理解】
课外兴趣小组活动时,老师提出了如下问题:
如图,△ABC中,若AB=8,AC=6,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:如图,延长AD到点E,使DE=AD,连结BE.请根据小明的方法思考:
(1)由已知和作图能得到的理由是( ).
A.SSS B.SAS C.AAS D.ASA
(2)AD的取值范围是( ).
A. B. C. D.
(3)【感悟】解题时,条件中若出现“中点”、“中线”字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论转化到同一个三角形中.
【问题解决】如图,AD是△ABC的中线,BE交AC于点E,交AD于F,且AE=EF.求证:AC=BF.
【答案】(1)B(2)C(3)见解析
【分析】(1)根据AD=DE,∠ADC=∠BDE,BD=DC推出△ADC和△EDB全等即可;
(2)根据全等得出BE=AC=6,AE=2AD,由三角形三边关系定理得出8-6<2AD<8+6,求出即可;
(3)延长AD到M,使AD=DM,连接BM,根据SAS证△ADC≌△MDB,推出BM=AC,∠CAD=∠M,根据AE=EF,推出∠CAD=∠AFE=∠BFD,求出∠BFD=∠M,根据等腰三角形的性质求出即可.
(1)∵在△ADC和△EDB中,∴△ADC≌△EDB(SAS),故选B;
(2)∵由(1)知:△ADC≌△EDB,∴BE=AC=6,AE=2AD,
∵在△ABE中,AB=8,由三角形三边关系定理得:8-6<2AD<8+6,∴1<AD<7,故选:C.
(3)延长AD到点M,使AD=DM,连接BM.
∵AD是△ABC中线∴CD=BD
∵在△ADC和△MDB中∴
∴BM=AC(全等三角形的对应边相等)
∠CAD=∠M(全等三角形的对应角相等)
∵AE=EF,∴∠CAD=∠AFE(等边对等角)
∵∠AFE=∠BFD,∴∠BFD=∠M,∴BF=BM(等角对等边)
又∵BM=AC,∴AC=BF.
【点评】本题考查了三角形的中线,三角形的三边关系定理,等腰三角形性质和判定,全等三角形的性质和判定等知识点,主要考查学生运用定理进行推理的能力.
【例1-2】【教材呈现】如图是华师版八年级上册数学教材第69页的部分内容:
如图,在中,D是边BC的中点,过点C画直线CE,使,交AD的延长线于点E,求证:
证明∵(已知)
∴,(两直线平行,内错角相等).
在与中,
∵,(已证),
(已知),
∴,
∴(全等三角形的对应边相等).
(1)【方法应用】如图①,在中,,,则BC边上的中线AD长度的取值范围是______.
(2)【猜想证明】如图②,在四边形ABCD中,,点E是BC的中点,若AE是的平分线,试猜想线段AB、AD、DC之间的数量关系,并证明你的猜想;
(3)【拓展延伸】如图③,已知,点E是BC的中点,点D在线段AE上,,若,,求出线段DF的长.
【答案】(1)1<AD<5;(2)AD=AB+DC.理由见解析;(3)DF=3.
【分析】(1)延长AD到E,使AD=DE,连接BE,证△ADC≌△EDB,推出AC=BE=4,在△ABE中,根据三角形三边关系定理得出AB-BE<AE<AB+BE,代入求出即可;
(2)结论:AD=AB+DC.延长AE,DC交于点F,证明△ABE≌△FEC(AAS),推出AB=CF,再证明DA=DF即可解决问题;(3)如图③,延长AE交CF的延长线于点G,证明AB=DF+CF,可得结论.
【详解】解:(1)延长AD到E,使AD=DE,连接BE,
∵AD是BC边上的中线,∴BD=CD,
在△ADC和△EDB中,,∴△ADC≌△EDB(SAS),∴AC=BE=4,
在△ABE中,AB-BE<AE<AB+BE,
∴6-4<2AD<6+4,∴1<AD<5,故答案为:1<AD<5;
(2)结论:AD=AB+DC.理由:如图②中,延长AE,DC交于点F,
∵AB∥CD,∴∠BAF=∠F,
在△ABE和△FCE中,,∴△ABE≌△FCE(AAS),∴CF=AB,
∵AE是∠BAD的平分线,∴∠BAF=∠FAD,∴∠FAD=∠F,∴AD=DF,
∵DC+CF=DF,∴DC+AB=AD;
(3)如图③,延长AE交CF的延长线于点G,
∵E是BC的中点,∴CE=BE,∵AB∥CF,∴∠BAE=∠G,
在△AEB和△GEC中,,∴△AEB≌△GEC(AAS),∴AB=GC,
∵∠EDF=∠BAE,∴∠FDG=∠G,∴FD=FG,∴AB=DF+CF,
∵AB=5,CF=2,∴DF=AB-CF=3.
【点评】本题考查了全等三角形的判定与性质、等腰三角形的判定与性质、角平分线的性质、三角形三边关系等知识点,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.
针对性训练1
1 .课外兴趣小组活动时,老师提出了如下问题:
(1)如图1,△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到点E,使DE=AD,请根据小明的方法思考帮小明完成解答过程.
(2)如图2,AD是△ABC的中线,BE交AC干E,交AD于F,且AE=EF.请判昕AC与BF的数量关系,并说明理由.
【答案】(1)见解析(2)AC=BF,理由见解析
【解析】(1)解:如图,延长AD到点E,使DE=AD,连接BE,
在△ADC和△EDB中∵,∴△ADC≌△EDB(SAS).∴BE=AC=3.
∵AB-BE(2)AC=BF,理由如下:延长AD至点G,使GD=AD,连接BG,
在△ADC和△GDB中,,∴△ADC≌△GDB(SAS).∴BG=AC,∠G=∠DAC..
∵AE=EF∴∠AFE=∠FAE. ∴∠DAC=∠AFE=∠BFG∴∠G=∠BFG∴BG=BF∴AC=BF.
【点评】本题考查全等三角形判定与性质,三角形三边的关系,作辅助线:延长AD到点E,使DE=AD,构造全等三角形是解题的关键.
2 .如图,在中,为边上的中线.
(1)按要求作图:延长到点E,使;连接.
(2)求证:.
(3)求证:.
(4)若,,求的取值范围.
【分析】(1)根据题目中语言描述画出图形即可;
(2)直接利用证明即可;
(3)根据,得,从而得出,再根据三角形三边关系即可得出,即可得出结论;
(4)根据三角形三边关系得,又由,,,,代入即可求解.
【详解】(1)解:如图所示,
(2)证明:如图,
∵为边上的中线,
∴,
在和中,
,
∴.
(3)证明:如图,
∵,
∴,
∵,
∴,
在中,,
∴.
(4)在中,
,
由(3)得 ,,
∵,,
∴,
∴,
∴.
【点拨】本题考查全等三角形的判定与性质,三角形三边的关系,熟练掌握全等三角形的判定与性质以及三角形三边的关系是解题的关键.
变式模型:
【例2-1】已知:如图,D为线段AB的中点,在AB上任取一点C(不与点A,B,D重合),分别以AC,BC为斜边在AB同侧作等腰Rt△ACE与等腰Rt△BCF,∠AEC=∠CFB=90°,连接DE,DF,EF.
(1)求∠ECF的度数;
(2)求证:△DEF为等腰直角三角形.
解析 (1)∵△ACE和△CBF均为等腰直角三角形,∴∠ECA=45°,∠FCB=45°.
∵∠ECA+∠ECF+∠FCB=180°,∴∠ECF=90°.
(2)证明:延长ED到点G,使得DG=DE,连接BG,FG.
∵D为线段AB的中点,∴AD=BD.
∵在△EDA和△GDB中,∴△EDA≌△GDB(SAS).
∴EA=GB,∠A=∠GBD=45°.
∵△ACE与△BCF是等腰直角三角形
∴CF=FB,AE=EC,∠A=∠ECA=∠FCB=∠FBC=45°.
∴CF=FB,EC=BG,∠ECF=90°.
∵在△ECF和△GBF中,∴△ECF≌△GBF(SAS).
∴EF=GF,∠EFC=∠GFB.
∵∠CFB=∠CFG+∠GFB=90°,∴∠EFG=∠EFC+∠CFG=90°.
∵在△EFD和△GFD中,∴△EFD≌△GFD.
∴∠EDF=∠GDF=90°,∠EFD=∠GFD=45°.
∴ED=DF,∴△DEF为等腰直角三角形.
【例2-2】.如图所示:△ABC是等边三角形,D、E分别是AB及AC延长线上的一点,且BD=CE,连接DE交BC于点M.求证:MD=ME.
证明 如图,过点E作EN∥AB,并交BC的延长线于N.
∵△ABC是等边三角形,∴∠B=∠ACB=60°.
又∵∠ACB与∠NCE是对顶角,∴∠ACB=∠NCE=60°.
∵AB∥NE,∴∠B=∠N=60°.
∴∠NCE=∠N=60°.
∴CE=NE.
又∵BD=CE,∴BD=NE.
在△BDM和△NEM中
∴△BDM≌△NEM(AAS).
∴DM=EM.
【例2-3】如图,在△ABC,AD平分∠BAC,E、F分别在BD、AD上,且DE=CD,EF=AC,求证:EF∥AB.
证明 过E作AC的平行线于AD延长线交于G点,
∵EG∥AC,∴∠DEG=∠C,
在△DEG和△DCA中,,∴△DEG≌△DCA(ASA),
∴EG=EF,∠G=∠CAD,又EF=AC
故EG=AC
∵AD平分∠BAC,∴∠BAD=∠CAD,
∵EG=EF,∴∠G=∠EFD,
∴∠EFD=∠BAD,∴EF∥AB.
针对性训练2
1.如图,点P为等边△ABC的边AB上一点,Q为BC延长线上一点,AP=CQ,PQ交AC于D,
(1)求证:DP=DQ;
(2)过P作PE⊥AC于E,若BC=4,求DE的长.
答案 (1)略 (2) 2
解析(1)证明:如图,过点P作PM∥BC,则∠DPM=∠Q,
∵△ABC为等边三角形,∴△APM是等边三角形,
∴AP=PM,
又∵AP=CQ,∴PM=CQ,
在△DPM和△DQC中,
∴△DPM≌△DQC(AAS),∴DP=DQ;
(2)∵△DPM≌△DQC,∴DM=DC,
∵PE⊥AC,△APM是等边三角形,∴AE=EM,
∴DE=DM+EM=AC,
∵等边三角形ABC的边BC=4,∴AC=4,
∴DE=×4=2.
如图,分别以△ABC的边AB,AC为一边在三角形外作正方形ABEF和ACGH,M为FH上的中点,求证:MA⊥BC.
证明 延长AM到N使MN=AM,如图,
∵M为FH上的中点,∴FM=HM,
在△AMF和△NMB中,,∴△AMF≌△NMB,
∴∠MAF=∠N,AF=NH,
∵四边形ABEF和四边形ACGH为正方形,
∴AB=AF,AC=AH,∠BAF=∠CAH=90°,
∴∠FAH+∠BAC=180°,HN=AB,
∴∠N+∠NAH+∠BAC=180°,
∵∠N+∠NAH+∠AHN=180°,∴∠BAC=∠AHN,
在△ABC和△HNA中,,∴△ABC≌△HNA(SAS),
∴∠ACB=∠HAN,
∵∠HAN+∠CAD=90°,∴∠ACD+∠CAD=90°,
∴∠ADC=90°,∴AD⊥BC.
巩固提高
1.是的中线,,则的取值可能是( )
A.3 B.6 C.8 D.12
【答案】A
【分析】先画出图形,延长至点,使得,连接,再利用定理证出,根据全等三角形的性质可得,然后根据三角形的三边关系定理即可得.
【详解】解:如图,延长至点,使得,连接,则,
是的中线,
,
在和中,,
,
,
在中,,即,
,
观察四个选项可知,只有A符合,
故选:A.
【点拨】本题考查了三角形全等的判定与性质、三角形的三边关系,通过作辅助线,构造全等三角形是解题关键.
2.如图,在中,为中线,且,则边的取值范围是___________.
【答案】
【分析】延长至,使得,连接,先证明,由此可得,,再根据三角形存在性,求得,即得到边的取值范围.
【详解】解:如图,延长至,使得,连接,
∵在中,为中线,
∴,
在与中,
∵,
∴,
∴.
∵,
又∵,,
∴,,
在中,
∵,
∵,,
∴,
故答案为:.
【点拨】本题考查了倍长中线构造全等三角形以及三角形存在性,掌握倍长中线法构造全等三角形是解题的关键.
3.如图,中,为的中点,是上一点,连接并延长交于,,且,,那么的长度为__.
【答案】;
【分析】延长至使,连接,得出,得出,所以得出是等腰三角形,根据已知线段长度建立等量关系计算.
【详解】
如图:延长至使,连接
在和中:
∴
∴
∵
∴
∴
∵
∴
∴
∴
即
∴
【点拨】倍长中线是常见的辅助线、全等中相关的角的代换是解决本题的关键.
4.规定:有两组边相等,且它们所夹的角互补的两个三角形叫兄弟三角形.如图,,,,回答下列问题:
(1)求证:和是兄弟三角形.
(2)取的中点P,连接,请证明.
【分析】(1)根据,,即可证明;
(2)延长至E,使,先证,推出,,进而推出,再证,即可推出,由此可证.
【详解】(1)证明:,
,
又,,
和是兄弟三角形.
(2)证明:延长至E,使,
P为的中点,
,
在和中,
,
,
,,
,
,
又,
,
,,
,
在和中,
,
,
又,
.
【点拨】本题考查全等三角形的判定与性质、平行线的判定与性质,解题的关键是正确作出辅助线,构造全等三角形.
5 .已知:如图,△ABC和△DEF,,,AP、DQ分别是BC和EF边上的高,且.求证:;
(2)如果(1)中的条件不变,“如图”二字去掉,那么△ABC与△DEF全等吗 如果全等请证明,如果不全等请举出反例.
(3)如果把(1)中的条件“AP、DQ分别是BC和EF边上的高”改为“AP、DQ分别是BC和EF边上的中线”,请证明:.
【答案】(1)见解析;(2)不一定全等;反例见解析;(3)证明见解析
【分析】(1)根据全等三角形的判定和性质证明即可;
(2)没有如图三角形的高线的位置不可知,所以无法求证;
(3)根据全等三角形的判定和性质证明即可.
【详解】解:(1)∵在△ABC和△DEF中,AP、DQ分别是三角形的高,
∴,,
在Rt△ABP和Rt△DEQ中,
,
∴(HL),
∴,
在Rt△ACP和Rt△DFQ中,
,
∴(HL).
∴,
∴,
即,
在△ABC和△DEF中,
∴(SAS);
(2)不一定全等,反例如图:
;
(3)延长AP至M,使得,延长DQ至N,使得.
∴,
∵
∴
∵AP、DQ是中线
∴,
在△ACP和△MBP中,
∴(SAS),
∴,
在△DFQ和△NEQ中,
∴△DFQ△NEQ(SAS),
∴,,
∵,
∴,
在△ABM和△DEN中,
∴△ABM△DEN(SSS),
∴,,
∴,
∴,
即,
在△ABC和△DEF中,
∴△ABC△DEF(SAS),
6 .(1)已知如图1,在中,,求边上的中线的取值范围.
(2)思考:已知如图2,是的中线,,试探究线段与的数量和位置关系,并加以证明.
【答案】(1);(2)且
【分析】(1)用倍长中线模型,构造全等三角形,即可求出中线的取值范围;
(2)用倍长中线模型,通过证明三角形的全等,可求出线段与的数量和位置关系.
【详解】解:(1)如下图,延长,使得,则,
∵D是的中点,
∴,
在和中,
,
∴,
∴,
在中,可得:,
即,
∵,
∴,
∴,
∴边上的中线的取值范围为:;
(2)且,证明如下:
如下图,延长,使得,延长与交于点H,
由(1)可易证,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
在和中,
,
∴,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
综上所述,且.
【点拨】本题考查三角形中线的定义、三角形全等的判定和性质,用倍长中线模型添加辅助线是解本题的关键,综合性较强,难度较大.
【点拨】本题考查了全等三角形的判定和性质,解决本题的关键是掌握三角形的高和中线的相关性质.
7.课堂上,老师出示了这样一个问题:
如图1,点D是△ABC边BC的中点,AB=5,AC=3,求AD的取值范围.
(1)小明的想法是,过点B作BE∥AC交AD的延长线于点E,如图2,从而通过构造全等解决问题,请你按照小明的想法解决此问题;
(2)请按照上述提示,解决下面问题:
在等腰Rt△ABC中,∠BAC=90°,AB=AC,点D是边AC延长线上一点,连接BD,过点A作AE⊥BD于点E,过点A作AF⊥AE,且AF=AE,连接EF交BC于点G,连接CF,求证BG=CG.
答案 (1)1<AD<4 (2)略
解析 (1)∵BE∥AC,∴∠C=∠EBD,
∵D是△ABC边BC的中点,∴CD=BD,
在△ACD和△EBD中,
∴△ACD≌△EBD(ASA),∴AC=BE=3,AD=ED,
∴AE=2AD,
在△ABE中,AB﹣BE<AE<AB+BE,即5﹣3<AE<5+3,
∴2<2AD<8,
∴1<AD<4;
(2)过C作CM∥BD交EF于M,如图:
∵AF⊥AE,且AF=AE,∴△AEF是等腰直角三角形,
∴∠AEF=∠AFE=45°,
∵∠BAC=90°,AF⊥AE,∴∠BAE=90°﹣∠EAC=∠CAF,
在△BAE和△CAF中,
∴△BAE≌△CAF(SAS),
∴∠AEB=∠AFC,BE=CF,
∴∠BEF=∠AEB+∠AEF=135°,
∵CM∥BD,∴∠CMG=∠BEF=135°,
∴∠FMC=45°,
∵AE⊥BD,∴∠AEB=∠AFC=90°,
∴∠CFM=∠AFC﹣∠AFE=45°,
∴∠FMC=∠CFM,
∴CF=CM,
∴BE=CM,
在△BEG和△CMG中,
∴△BEG≌△CMG(AAS),
∴BG=CG.
8.如图,△ABC中,BD=DC=AC,E是DC的中点,求证:AB=2AE.
证明:延长AE到F,使EF=AE,连结DF,
∵E是DC中点,∴DE=CE,
在△DEF和△CEA中,
∴△DEF≌△CEA(SAS),
∴DF=AC=BD,∠FDE=∠C,
∵DC=AC,∴∠ADC=∠CAD,
∵∠ADB=∠C+∠CAD,∠ADF=∠FDE+∠ADC,
∴∠ADF=∠ADB,
在△ADB和△ADF中,
∴△ADB≌△ADF(SAS)
∴AB=AF=2AE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
八年级数学上分层优化堂堂清
十二章 全等三角形
12.2三角形全等的重要模型
倍长中线模型
学习目标:
了解倍长中线法的基本方法。
会运用倍长中线法构造全等三角形证明和计算;
3、提高推理能力,获得成功的体验,增强学习的自信心。
老师对你说:
全等三角形在中考数学几何模块中占据着重要地位,也是学生必须掌握的一块内容,本专题就全等三角形中的重要模型--倍长中线模型进行梳理及对应试题分析,方便掌握。
全等三角形的对应边相等,对应角相等是证线段相等或角相等的重要依据,在解题过程中若不能直接运用,则需要通过作辅助线来构造全等三角形,若已知条件中存在中线,可将中线延长,将要求解或证明的结论进行转化,进而解决问题。
倍长中线法定义
延长三角形的中线,使得延长后的线段是原中线的两倍.
其目的是构造一对对顶的全等三角形;其本质是转移边和角.
示例剖析
其中,延长使得,则.
其模型也属于“字型或成字型”.
基本模式:
1.基本型:如图1,在三角形ABC中,AD为BC边上的中线.
证明思路:延长AD至点E,使得AD=DE. 若连结BE,则;若连结EC,则;
2、中点型:如图2,为的中点.
证明思路:若延长至点,使得,连结,则;
若延长至点,使得,连结,则.
3、中点+平行线型:如图3, ,点为线段的中点.
证明思路:延长交于点 (或交延长线于点),则.
【例1-1】【阅读理解】
课外兴趣小组活动时,老师提出了如下问题:
如图,△ABC中,若AB=8,AC=6,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:如图,延长AD到点E,使DE=AD,连结BE.请根据小明的方法思考:
(1)由已知和作图能得到的理由是( ).
A.SSS B.SAS C.AAS D.ASA
(2)AD的取值范围是( ).
A. B. C. D.
(3)【感悟】解题时,条件中若出现“中点”、“中线”字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论转化到同一个三角形中.
【问题解决】如图,AD是△ABC的中线,BE交AC于点E,交AD于F,且AE=EF.求证:AC=BF.
【例1-2】【教材呈现】如图是华师版八年级上册数学教材第69页的部分内容:
如图,在中,D是边BC的中点,过点C画直线CE,使,交AD的延长线于点E,求证:
证明∵(已知)
∴,(两直线平行,内错角相等).
在与中,
∵,(已证),
(已知),
∴,
∴(全等三角形的对应边相等).
(1)【方法应用】如图①,在中,,,则BC边上的中线AD长度的取值范围是______.
(2)【猜想证明】如图②,在四边形ABCD中,,点E是BC的中点,若AE是的平分线,试猜想线段AB、AD、DC之间的数量关系,并证明你的猜想;
(3)【拓展延伸】如图③,已知,点E是BC的中点,点D在线段AE上,,若,,求出线段DF的长.
针对性训练1
1 .课外兴趣小组活动时,老师提出了如下问题:
(1)如图1,△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到点E,使DE=AD,请根据小明的方法思考帮小明完成解答过程.
(2)如图2,AD是△ABC的中线,BE交AC干E,交AD于F,且AE=EF.请判昕AC与BF的数量关系,并说明理由.
2 .如图,在中,为边上的中线.
(1)按要求作图:延长到点E,使;连接.
(2)求证:.
(3)求证:.
(4)若,,求的取值范围.
变式模型:
【例2-1】已知:如图,D为线段AB的中点,在AB上任取一点C(不与点A,B,D重合),分别以AC,BC为斜边在AB同侧作等腰Rt△ACE与等腰Rt△BCF,∠AEC=∠CFB=90°,连接DE,DF,EF.
(1)求∠ECF的度数;
(2)求证:△DEF为等腰直角三角形.
【例2-2】.如图所示:△ABC是等边三角形,D、E分别是AB及AC延长线上的一点,且BD=CE,连接DE交BC于点M.求证:MD=ME.
【例2-3】如图,在△ABC,AD平分∠BAC,E、F分别在BD、AD上,且DE=CD,EF=AC,求证:EF∥AB.
针对性训练2
1.如图,点P为等边△ABC的边AB上一点,Q为BC延长线上一点,AP=CQ,PQ交AC于D,
(1)求证:DP=DQ;
(2)过P作PE⊥AC于E,若BC=4,求DE的长.
2 .如图,分别以△ABC的边AB,AC为一边在三角形外作正方形ABEF和ACGH,M为FH上的中点,求证:MA⊥BC.
巩固提高
1.是的中线,,则的取值可能是( )
A.3 B.6 C.8 D.12
2.如图,在中,为中线,且,则边的取值范围是___________.
3.如图,中,为的中点,是上一点,连接并延长交于,,且,,那么的长度为__.
4.规定:有两组边相等,且它们所夹的角互补的两个三角形叫兄弟三角形.如图,,,,回答下列问题:
(1)求证:和是兄弟三角形.
(2)取的中点P,连接,请证明.
5 .已知:如图,△ABC和△DEF,,,AP、DQ分别是BC和EF边上的高,且.求证:;
(2)如果(1)中的条件不变,“如图”二字去掉,那么△ABC与△DEF全等吗 如果全等请证明,如果不全等请举出反例.
(3)如果把(1)中的条件“AP、DQ分别是BC和EF边上的高”改为“AP、DQ分别是BC和EF边上的中线”,请证明:.
6 .(1)已知如图1,在中,,求边上的中线的取值范围.
(2)思考:已知如图2,是的中线,,试探究线段与的数量和位置关系,并加以证明.
7.课堂上,老师出示了这样一个问题:
如图1,点D是△ABC边BC的中点,AB=5,AC=3,求AD的取值范围.
(1)小明的想法是,过点B作BE∥AC交AD的延长线于点E,如图2,从而通过构造全等解决问题,请你按照小明的想法解决此问题;
(2)请按照上述提示,解决下面问题:
在等腰Rt△ABC中,∠BAC=90°,AB=AC,点D是边AC延长线上一点,连接BD,过点A作AE⊥BD于点E,过点A作AF⊥AE,且AF=AE,连接EF交BC于点G,连接CF,求证BG=CG.
8.如图,△ABC中,BD=DC=AC,E是DC的中点,求证:AB=2AE.
八年级数学上分层优化堂堂清
十二章 全等三角形
12.2三角形全等的重要模型
倍长中线模型(解析版)
学习目标:
了解倍长中线法的基本方法。
会运用倍长中线法构造全等三角形证明和计算;
3、提高推理能力,获得成功的体验,增强学习的自信心。
老师对你说:
全等三角形在中考数学几何模块中占据着重要地位,也是学生必须掌握的一块内容,本专题就全等三角形中的重要模型--倍长中线模型进行梳理及对应试题分析,方便掌握。
全等三角形的对应边相等,对应角相等是证线段相等或角相等的重要依据,在解题过程中若不能直接运用,则需要通过作辅助线来构造全等三角形,若已知条件中存在中线,可将中线延长,将要求解或证明的结论进行转化,进而解决问题。
倍长中线法定义
延长三角形的中线,使得延长后的线段是原中线的两倍.
其目的是构造一对对顶的全等三角形;其本质是转移边和角.
示例剖析
其中,延长使得,则.
其模型也属于“字型或成字型”.
基本方法:
1.基本型:如图1,在三角形ABC中,AD为BC边上的中线.
证明思路:延长AD至点E,使得AD=DE. 若连结BE,则;若连结EC,则;
2、中点型:如图2,为的中点.
证明思路:若延长至点,使得,连结,则;
若延长至点,使得,连结,则.
3、中点+平行线型:如图3, ,点为线段的中点.
证明思路:延长交于点 (或交延长线于点),则.
【例1-1】【阅读理解】
课外兴趣小组活动时,老师提出了如下问题:
如图,△ABC中,若AB=8,AC=6,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:如图,延长AD到点E,使DE=AD,连结BE.请根据小明的方法思考:
(1)由已知和作图能得到的理由是( ).
A.SSS B.SAS C.AAS D.ASA
(2)AD的取值范围是( ).
A. B. C. D.
(3)【感悟】解题时,条件中若出现“中点”、“中线”字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论转化到同一个三角形中.
【问题解决】如图,AD是△ABC的中线,BE交AC于点E,交AD于F,且AE=EF.求证:AC=BF.
【答案】(1)B(2)C(3)见解析
【分析】(1)根据AD=DE,∠ADC=∠BDE,BD=DC推出△ADC和△EDB全等即可;
(2)根据全等得出BE=AC=6,AE=2AD,由三角形三边关系定理得出8-6<2AD<8+6,求出即可;
(3)延长AD到M,使AD=DM,连接BM,根据SAS证△ADC≌△MDB,推出BM=AC,∠CAD=∠M,根据AE=EF,推出∠CAD=∠AFE=∠BFD,求出∠BFD=∠M,根据等腰三角形的性质求出即可.
(1)∵在△ADC和△EDB中,∴△ADC≌△EDB(SAS),故选B;
(2)∵由(1)知:△ADC≌△EDB,∴BE=AC=6,AE=2AD,
∵在△ABE中,AB=8,由三角形三边关系定理得:8-6<2AD<8+6,∴1<AD<7,故选:C.
(3)延长AD到点M,使AD=DM,连接BM.
∵AD是△ABC中线∴CD=BD
∵在△ADC和△MDB中∴
∴BM=AC(全等三角形的对应边相等)
∠CAD=∠M(全等三角形的对应角相等)
∵AE=EF,∴∠CAD=∠AFE(等边对等角)
∵∠AFE=∠BFD,∴∠BFD=∠M,∴BF=BM(等角对等边)
又∵BM=AC,∴AC=BF.
【点评】本题考查了三角形的中线,三角形的三边关系定理,等腰三角形性质和判定,全等三角形的性质和判定等知识点,主要考查学生运用定理进行推理的能力.
【例1-2】【教材呈现】如图是华师版八年级上册数学教材第69页的部分内容:
如图,在中,D是边BC的中点,过点C画直线CE,使,交AD的延长线于点E,求证:
证明∵(已知)
∴,(两直线平行,内错角相等).
在与中,
∵,(已证),
(已知),
∴,
∴(全等三角形的对应边相等).
(1)【方法应用】如图①,在中,,,则BC边上的中线AD长度的取值范围是______.
(2)【猜想证明】如图②,在四边形ABCD中,,点E是BC的中点,若AE是的平分线,试猜想线段AB、AD、DC之间的数量关系,并证明你的猜想;
(3)【拓展延伸】如图③,已知,点E是BC的中点,点D在线段AE上,,若,,求出线段DF的长.
【答案】(1)1<AD<5;(2)AD=AB+DC.理由见解析;(3)DF=3.
【分析】(1)延长AD到E,使AD=DE,连接BE,证△ADC≌△EDB,推出AC=BE=4,在△ABE中,根据三角形三边关系定理得出AB-BE<AE<AB+BE,代入求出即可;
(2)结论:AD=AB+DC.延长AE,DC交于点F,证明△ABE≌△FEC(AAS),推出AB=CF,再证明DA=DF即可解决问题;(3)如图③,延长AE交CF的延长线于点G,证明AB=DF+CF,可得结论.
【详解】解:(1)延长AD到E,使AD=DE,连接BE,
∵AD是BC边上的中线,∴BD=CD,
在△ADC和△EDB中,,∴△ADC≌△EDB(SAS),∴AC=BE=4,
在△ABE中,AB-BE<AE<AB+BE,
∴6-4<2AD<6+4,∴1<AD<5,故答案为:1<AD<5;
(2)结论:AD=AB+DC.理由:如图②中,延长AE,DC交于点F,
∵AB∥CD,∴∠BAF=∠F,
在△ABE和△FCE中,,∴△ABE≌△FCE(AAS),∴CF=AB,
∵AE是∠BAD的平分线,∴∠BAF=∠FAD,∴∠FAD=∠F,∴AD=DF,
∵DC+CF=DF,∴DC+AB=AD;
(3)如图③,延长AE交CF的延长线于点G,
∵E是BC的中点,∴CE=BE,∵AB∥CF,∴∠BAE=∠G,
在△AEB和△GEC中,,∴△AEB≌△GEC(AAS),∴AB=GC,
∵∠EDF=∠BAE,∴∠FDG=∠G,∴FD=FG,∴AB=DF+CF,
∵AB=5,CF=2,∴DF=AB-CF=3.
【点评】本题考查了全等三角形的判定与性质、等腰三角形的判定与性质、角平分线的性质、三角形三边关系等知识点,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.
针对性训练1
1 .课外兴趣小组活动时,老师提出了如下问题:
(1)如图1,△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到点E,使DE=AD,请根据小明的方法思考帮小明完成解答过程.
(2)如图2,AD是△ABC的中线,BE交AC干E,交AD于F,且AE=EF.请判昕AC与BF的数量关系,并说明理由.
【答案】(1)见解析(2)AC=BF,理由见解析
【解析】(1)解:如图,延长AD到点E,使DE=AD,连接BE,
在△ADC和△EDB中∵,∴△ADC≌△EDB(SAS).∴BE=AC=3.
∵AB-BE
在△ADC和△GDB中,,∴△ADC≌△GDB(SAS).∴BG=AC,∠G=∠DAC..
∵AE=EF∴∠AFE=∠FAE. ∴∠DAC=∠AFE=∠BFG∴∠G=∠BFG∴BG=BF∴AC=BF.
【点评】本题考查全等三角形判定与性质,三角形三边的关系,作辅助线:延长AD到点E,使DE=AD,构造全等三角形是解题的关键.
2 .如图,在中,为边上的中线.
(1)按要求作图:延长到点E,使;连接.
(2)求证:.
(3)求证:.
(4)若,,求的取值范围.
【分析】(1)根据题目中语言描述画出图形即可;
(2)直接利用证明即可;
(3)根据,得,从而得出,再根据三角形三边关系即可得出,即可得出结论;
(4)根据三角形三边关系得,又由,,,,代入即可求解.
【详解】(1)解:如图所示,
(2)证明:如图,
∵为边上的中线,
∴,
在和中,
,
∴.
(3)证明:如图,
∵,
∴,
∵,
∴,
在中,,
∴.
(4)在中,
,
由(3)得 ,,
∵,,
∴,
∴,
∴.
【点拨】本题考查全等三角形的判定与性质,三角形三边的关系,熟练掌握全等三角形的判定与性质以及三角形三边的关系是解题的关键.
变式模型:
【例2-1】已知:如图,D为线段AB的中点,在AB上任取一点C(不与点A,B,D重合),分别以AC,BC为斜边在AB同侧作等腰Rt△ACE与等腰Rt△BCF,∠AEC=∠CFB=90°,连接DE,DF,EF.
(1)求∠ECF的度数;
(2)求证:△DEF为等腰直角三角形.
解析 (1)∵△ACE和△CBF均为等腰直角三角形,∴∠ECA=45°,∠FCB=45°.
∵∠ECA+∠ECF+∠FCB=180°,∴∠ECF=90°.
(2)证明:延长ED到点G,使得DG=DE,连接BG,FG.
∵D为线段AB的中点,∴AD=BD.
∵在△EDA和△GDB中,∴△EDA≌△GDB(SAS).
∴EA=GB,∠A=∠GBD=45°.
∵△ACE与△BCF是等腰直角三角形
∴CF=FB,AE=EC,∠A=∠ECA=∠FCB=∠FBC=45°.
∴CF=FB,EC=BG,∠ECF=90°.
∵在△ECF和△GBF中,∴△ECF≌△GBF(SAS).
∴EF=GF,∠EFC=∠GFB.
∵∠CFB=∠CFG+∠GFB=90°,∴∠EFG=∠EFC+∠CFG=90°.
∵在△EFD和△GFD中,∴△EFD≌△GFD.
∴∠EDF=∠GDF=90°,∠EFD=∠GFD=45°.
∴ED=DF,∴△DEF为等腰直角三角形.
【例2-2】.如图所示:△ABC是等边三角形,D、E分别是AB及AC延长线上的一点,且BD=CE,连接DE交BC于点M.求证:MD=ME.
证明 如图,过点E作EN∥AB,并交BC的延长线于N.
∵△ABC是等边三角形,∴∠B=∠ACB=60°.
又∵∠ACB与∠NCE是对顶角,∴∠ACB=∠NCE=60°.
∵AB∥NE,∴∠B=∠N=60°.
∴∠NCE=∠N=60°.
∴CE=NE.
又∵BD=CE,∴BD=NE.
在△BDM和△NEM中
∴△BDM≌△NEM(AAS).
∴DM=EM.
【例2-3】如图,在△ABC,AD平分∠BAC,E、F分别在BD、AD上,且DE=CD,EF=AC,求证:EF∥AB.
证明 过E作AC的平行线于AD延长线交于G点,
∵EG∥AC,∴∠DEG=∠C,
在△DEG和△DCA中,,∴△DEG≌△DCA(ASA),
∴EG=EF,∠G=∠CAD,又EF=AC
故EG=AC
∵AD平分∠BAC,∴∠BAD=∠CAD,
∵EG=EF,∴∠G=∠EFD,
∴∠EFD=∠BAD,∴EF∥AB.
针对性训练2
1.如图,点P为等边△ABC的边AB上一点,Q为BC延长线上一点,AP=CQ,PQ交AC于D,
(1)求证:DP=DQ;
(2)过P作PE⊥AC于E,若BC=4,求DE的长.
答案 (1)略 (2) 2
解析(1)证明:如图,过点P作PM∥BC,则∠DPM=∠Q,
∵△ABC为等边三角形,∴△APM是等边三角形,
∴AP=PM,
又∵AP=CQ,∴PM=CQ,
在△DPM和△DQC中,
∴△DPM≌△DQC(AAS),∴DP=DQ;
(2)∵△DPM≌△DQC,∴DM=DC,
∵PE⊥AC,△APM是等边三角形,∴AE=EM,
∴DE=DM+EM=AC,
∵等边三角形ABC的边BC=4,∴AC=4,
∴DE=×4=2.
如图,分别以△ABC的边AB,AC为一边在三角形外作正方形ABEF和ACGH,M为FH上的中点,求证:MA⊥BC.
证明 延长AM到N使MN=AM,如图,
∵M为FH上的中点,∴FM=HM,
在△AMF和△NMB中,,∴△AMF≌△NMB,
∴∠MAF=∠N,AF=NH,
∵四边形ABEF和四边形ACGH为正方形,
∴AB=AF,AC=AH,∠BAF=∠CAH=90°,
∴∠FAH+∠BAC=180°,HN=AB,
∴∠N+∠NAH+∠BAC=180°,
∵∠N+∠NAH+∠AHN=180°,∴∠BAC=∠AHN,
在△ABC和△HNA中,,∴△ABC≌△HNA(SAS),
∴∠ACB=∠HAN,
∵∠HAN+∠CAD=90°,∴∠ACD+∠CAD=90°,
∴∠ADC=90°,∴AD⊥BC.
巩固提高
1.是的中线,,则的取值可能是( )
A.3 B.6 C.8 D.12
【答案】A
【分析】先画出图形,延长至点,使得,连接,再利用定理证出,根据全等三角形的性质可得,然后根据三角形的三边关系定理即可得.
【详解】解:如图,延长至点,使得,连接,则,
是的中线,
,
在和中,,
,
,
在中,,即,
,
观察四个选项可知,只有A符合,
故选:A.
【点拨】本题考查了三角形全等的判定与性质、三角形的三边关系,通过作辅助线,构造全等三角形是解题关键.
2.如图,在中,为中线,且,则边的取值范围是___________.
【答案】
【分析】延长至,使得,连接,先证明,由此可得,,再根据三角形存在性,求得,即得到边的取值范围.
【详解】解:如图,延长至,使得,连接,
∵在中,为中线,
∴,
在与中,
∵,
∴,
∴.
∵,
又∵,,
∴,,
在中,
∵,
∵,,
∴,
故答案为:.
【点拨】本题考查了倍长中线构造全等三角形以及三角形存在性,掌握倍长中线法构造全等三角形是解题的关键.
3.如图,中,为的中点,是上一点,连接并延长交于,,且,,那么的长度为__.
【答案】;
【分析】延长至使,连接,得出,得出,所以得出是等腰三角形,根据已知线段长度建立等量关系计算.
【详解】
如图:延长至使,连接
在和中:
∴
∴
∵
∴
∴
∵
∴
∴
∴
即
∴
【点拨】倍长中线是常见的辅助线、全等中相关的角的代换是解决本题的关键.
4.规定:有两组边相等,且它们所夹的角互补的两个三角形叫兄弟三角形.如图,,,,回答下列问题:
(1)求证:和是兄弟三角形.
(2)取的中点P,连接,请证明.
【分析】(1)根据,,即可证明;
(2)延长至E,使,先证,推出,,进而推出,再证,即可推出,由此可证.
【详解】(1)证明:,
,
又,,
和是兄弟三角形.
(2)证明:延长至E,使,
P为的中点,
,
在和中,
,
,
,,
,
,
又,
,
,,
,
在和中,
,
,
又,
.
【点拨】本题考查全等三角形的判定与性质、平行线的判定与性质,解题的关键是正确作出辅助线,构造全等三角形.
5 .已知:如图,△ABC和△DEF,,,AP、DQ分别是BC和EF边上的高,且.求证:;
(2)如果(1)中的条件不变,“如图”二字去掉,那么△ABC与△DEF全等吗 如果全等请证明,如果不全等请举出反例.
(3)如果把(1)中的条件“AP、DQ分别是BC和EF边上的高”改为“AP、DQ分别是BC和EF边上的中线”,请证明:.
【答案】(1)见解析;(2)不一定全等;反例见解析;(3)证明见解析
【分析】(1)根据全等三角形的判定和性质证明即可;
(2)没有如图三角形的高线的位置不可知,所以无法求证;
(3)根据全等三角形的判定和性质证明即可.
【详解】解:(1)∵在△ABC和△DEF中,AP、DQ分别是三角形的高,
∴,,
在Rt△ABP和Rt△DEQ中,
,
∴(HL),
∴,
在Rt△ACP和Rt△DFQ中,
,
∴(HL).
∴,
∴,
即,
在△ABC和△DEF中,
∴(SAS);
(2)不一定全等,反例如图:
;
(3)延长AP至M,使得,延长DQ至N,使得.
∴,
∵
∴
∵AP、DQ是中线
∴,
在△ACP和△MBP中,
∴(SAS),
∴,
在△DFQ和△NEQ中,
∴△DFQ△NEQ(SAS),
∴,,
∵,
∴,
在△ABM和△DEN中,
∴△ABM△DEN(SSS),
∴,,
∴,
∴,
即,
在△ABC和△DEF中,
∴△ABC△DEF(SAS),
6 .(1)已知如图1,在中,,求边上的中线的取值范围.
(2)思考:已知如图2,是的中线,,试探究线段与的数量和位置关系,并加以证明.
【答案】(1);(2)且
【分析】(1)用倍长中线模型,构造全等三角形,即可求出中线的取值范围;
(2)用倍长中线模型,通过证明三角形的全等,可求出线段与的数量和位置关系.
【详解】解:(1)如下图,延长,使得,则,
∵D是的中点,
∴,
在和中,
,
∴,
∴,
在中,可得:,
即,
∵,
∴,
∴,
∴边上的中线的取值范围为:;
(2)且,证明如下:
如下图,延长,使得,延长与交于点H,
由(1)可易证,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
在和中,
,
∴,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
综上所述,且.
【点拨】本题考查三角形中线的定义、三角形全等的判定和性质,用倍长中线模型添加辅助线是解本题的关键,综合性较强,难度较大.
【点拨】本题考查了全等三角形的判定和性质,解决本题的关键是掌握三角形的高和中线的相关性质.
7.课堂上,老师出示了这样一个问题:
如图1,点D是△ABC边BC的中点,AB=5,AC=3,求AD的取值范围.
(1)小明的想法是,过点B作BE∥AC交AD的延长线于点E,如图2,从而通过构造全等解决问题,请你按照小明的想法解决此问题;
(2)请按照上述提示,解决下面问题:
在等腰Rt△ABC中,∠BAC=90°,AB=AC,点D是边AC延长线上一点,连接BD,过点A作AE⊥BD于点E,过点A作AF⊥AE,且AF=AE,连接EF交BC于点G,连接CF,求证BG=CG.
答案 (1)1<AD<4 (2)略
解析 (1)∵BE∥AC,∴∠C=∠EBD,
∵D是△ABC边BC的中点,∴CD=BD,
在△ACD和△EBD中,
∴△ACD≌△EBD(ASA),∴AC=BE=3,AD=ED,
∴AE=2AD,
在△ABE中,AB﹣BE<AE<AB+BE,即5﹣3<AE<5+3,
∴2<2AD<8,
∴1<AD<4;
(2)过C作CM∥BD交EF于M,如图:
∵AF⊥AE,且AF=AE,∴△AEF是等腰直角三角形,
∴∠AEF=∠AFE=45°,
∵∠BAC=90°,AF⊥AE,∴∠BAE=90°﹣∠EAC=∠CAF,
在△BAE和△CAF中,
∴△BAE≌△CAF(SAS),
∴∠AEB=∠AFC,BE=CF,
∴∠BEF=∠AEB+∠AEF=135°,
∵CM∥BD,∴∠CMG=∠BEF=135°,
∴∠FMC=45°,
∵AE⊥BD,∴∠AEB=∠AFC=90°,
∴∠CFM=∠AFC﹣∠AFE=45°,
∴∠FMC=∠CFM,
∴CF=CM,
∴BE=CM,
在△BEG和△CMG中,
∴△BEG≌△CMG(AAS),
∴BG=CG.
8.如图,△ABC中,BD=DC=AC,E是DC的中点,求证:AB=2AE.
证明:延长AE到F,使EF=AE,连结DF,
∵E是DC中点,∴DE=CE,
在△DEF和△CEA中,
∴△DEF≌△CEA(SAS),
∴DF=AC=BD,∠FDE=∠C,
∵DC=AC,∴∠ADC=∠CAD,
∵∠ADB=∠C+∠CAD,∠ADF=∠FDE+∠ADC,
∴∠ADF=∠ADB,
在△ADB和△ADF中,
∴△ADB≌△ADF(SAS)
∴AB=AF=2AE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
