几种不同增长的函数模型
图片预览




文档简介
课件14张PPT。3.2.1几种不同增长的函数模型分析我们知道,函数是描述客观世界变化规律的基本数学模型,
不同的变化规律需要用不同的函数模型来描述。那么,面
临一个实际问题,应当如何选择恰当的函数模型来刻画呢?下面我们来看两个具体问题例1假设你有一笔资金用于投资,现有三种投资方案供你选择,
这三个方案的回报如下方案一:每天回报40元方案二:每天回报10元,以后每天比前一天多回报10元方案三:每天回报0.4元,以后每天比前一天翻一番请问,你会选择那种投资呢?我们可以先建立三种投资方案所对应的函数模型,再通过
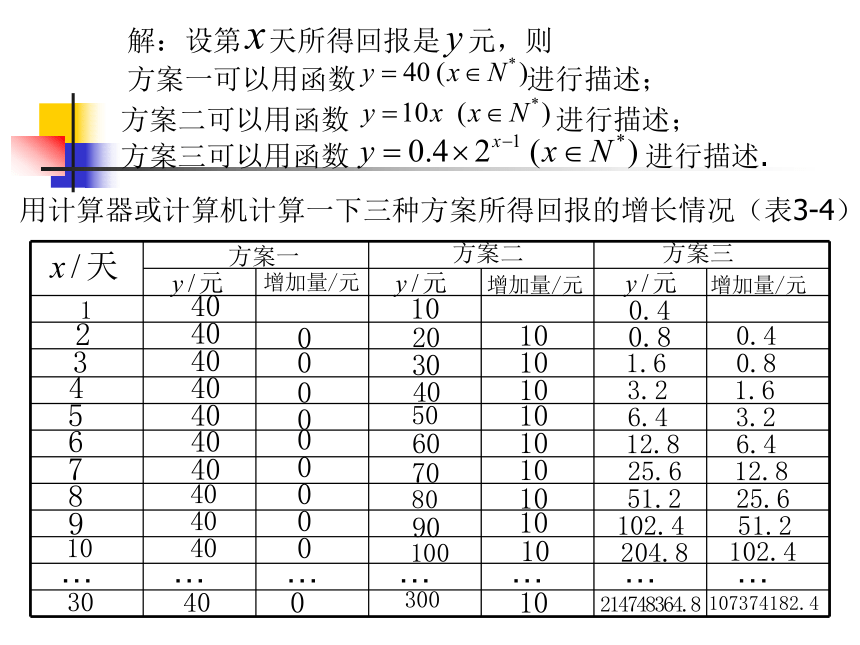
比较它们的增长情况,为选择投资方案提供一依据方案一可以用函数 进行描述;解:设第 天所得回报是 元,则方案二可以用函数 进行描述;方案三可以用函数 进行描述.用计算器或计算机计算一下三种方案所得回报的增长情况(表3-4)方案一方案二方案三由表3-4和图3.2-1可知,方案一的
函数是常数函数,方案二、方案三
的函数都是增函数,但是方案三的
函数与方案二的函数的增长情况是
不同的。可以看到,尽管方案一、
方案二在第一天所得回报分别是方
案三的100倍和25倍,但它的增长
量固定不变,二方案三是“指数增长”
其“增长量”是成倍增加的,从第七天
开始,方案三比其他两个方案增长快
得多,这种增长速度是方案一、方案
二所无法企及的。从每天所得回报看,
在第1~3天,方案一最多;在第4天
方案一和方案二一样多,方案三最少;
在第5~8天,方案二最多;第9天开
始,方案三比其他两个方案所得回
报多得多,到第30天,所得回报已
超过2亿元。
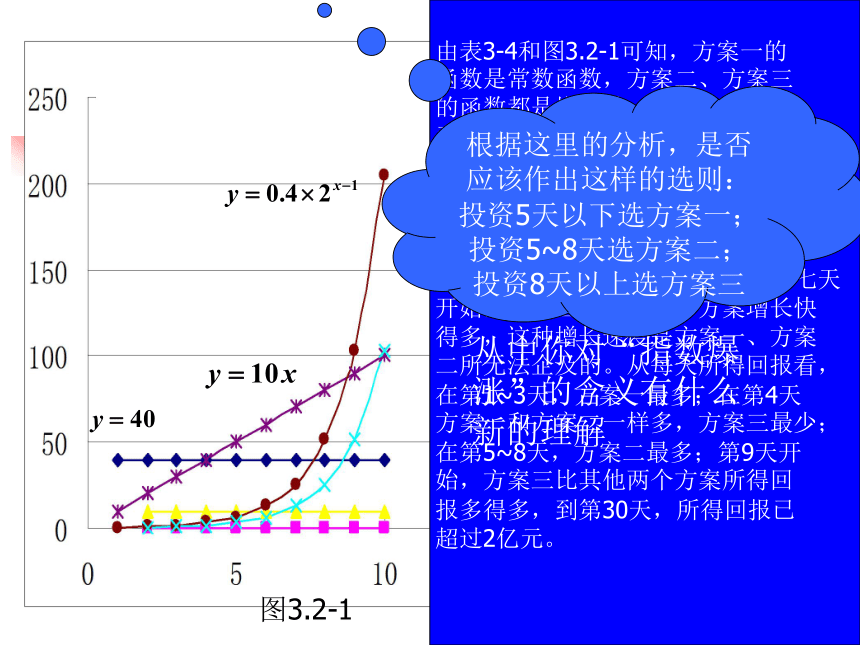
我们看到,底数为2的指数函数模型比线性函数模型增长速度要快得多。
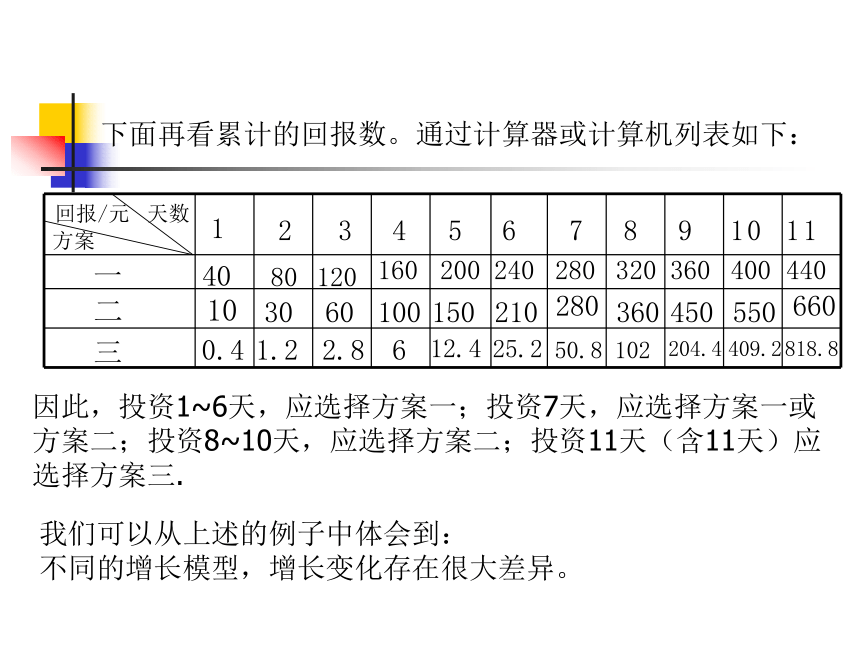
从中你对“指数爆涨”的含义有什么新的理解图3.2-1根据这里的分析,是否应该作出这样的选则:投资5天以下选方案一;投资5~8天选方案二;投资8天以上选方案三下面再看累计的回报数。通过计算器或计算机列表如下:因此,投资1~6天,应选择方案一;投资7天,应选择方案一或
方案二;投资8~10天,应选择方案二;投资11天(含11天)应
选择方案三.我们可以从上述的例子中体会到:
不同的增长模型,增长变化存在很大差异。分析例2某公司为了实现1000万元利润的目标,准备制定一个激励
销售人员的奖励方案:在销售利润达到10万元时,按销售利润
进行奖励,且奖金 (单位:万元)随销售利润 (单位:万元)
的增加而增加,但奖金总数不超过5万元,同时奖金不超过利润
的25%。现有三个奖励模型:
其中哪个模型能符合公司的要求?某个奖励模型符合公司要求,就是依据这个模型进行奖励时,
奖金总数不超过5万元,同时奖金不超过利润的25%,由于公
司总的利润目标为1000万元,所以人员销售利润一般不会超过
公司总的利润。于是,只需在区间[10,100]上,检验三个模型
是否符合公司要求即可。
不妨先作函数图象,通过观察函数的图象,得到初步的结论,
再通过具体计算,确认结果解:借助计算器或计算机作出函数
的图象(图3.2-2)观察图象发现,在区间[10,100]上,模型 的图象都有一部分在直线y=5的上方,只有模型
的图象始终在y=5的下方,这说明只有按模型
进行奖励时才符合公司的要求。下面通过计算确认上述判断.对于模型 ,它在[10,1000]上递增,而当时, ,因此当 时,首先计算哪个模型的奖金总数不超过5万所以该模型不符合要求;对于模型 由函数图象,并利用计算器,可知在区间(805,806)内有一个点 满足 ,由于它在区间[10,1000]上递增,因此当 时,所以该模型不符合要求;对于模型 ,它在区间[10,1000]上递增,而且当 时, ,所以它符合奖金总数不超过5万元的要求.再计算按模型 奖励时奖金是否不超过利润的25%,即当 时,是否有令利用计算器或计算机作出函数 的图象(图3.2-3),由图象可知它是递减的,因此综上所述,模型 确实能符合公司要求即所以当 时,说明按模型 奖励,奖金不会超过利润的25%练习1、四个变量 随变量 变化的数据如下表:关于 呈指数型函数变化的变量是2、某种计算机病毒是通过电子邮件进行传播的,如果某台计算机
感染上这种病毒,那么它就会在下一轮病毒发作时传播一次病毒,
并感染其他20台未感染病毒的计算机。现有10台计算即被第一轮
病毒感染,问被第五轮病毒感染的计算机共有多少台?我们知道,对于函数 ,指数函数
与幂函数 在区间 上都是增函数。从上述
两个例子可以看到,这三类函数的增长是有差异的。那么,这种差异的具体情况到底怎样呢?下面,我们不妨先以函数 为例进行研究利用计算器或计算机,列出自变量与函数值的对应值表(表3-5),
并在同一平面直角坐标系内画出三个函数的图象(表3.2-4)。可以
看到,虽然它们都是增函数,但它们的增长速度是不同的。表3-5观察请在图象上分别标出是不等式 成立的自变量
的取值范围表3-6表3-7探究结论:探究你能用同样的访法,讨论一下函数 ,
, 在区间 上的衰减情况吗?
在同一平面直角坐标系内作出下列函数图象,并比较它们的增长情况练习
不同的变化规律需要用不同的函数模型来描述。那么,面
临一个实际问题,应当如何选择恰当的函数模型来刻画呢?下面我们来看两个具体问题例1假设你有一笔资金用于投资,现有三种投资方案供你选择,
这三个方案的回报如下方案一:每天回报40元方案二:每天回报10元,以后每天比前一天多回报10元方案三:每天回报0.4元,以后每天比前一天翻一番请问,你会选择那种投资呢?我们可以先建立三种投资方案所对应的函数模型,再通过
比较它们的增长情况,为选择投资方案提供一依据方案一可以用函数 进行描述;解:设第 天所得回报是 元,则方案二可以用函数 进行描述;方案三可以用函数 进行描述.用计算器或计算机计算一下三种方案所得回报的增长情况(表3-4)方案一方案二方案三由表3-4和图3.2-1可知,方案一的
函数是常数函数,方案二、方案三
的函数都是增函数,但是方案三的
函数与方案二的函数的增长情况是
不同的。可以看到,尽管方案一、
方案二在第一天所得回报分别是方
案三的100倍和25倍,但它的增长
量固定不变,二方案三是“指数增长”
其“增长量”是成倍增加的,从第七天
开始,方案三比其他两个方案增长快
得多,这种增长速度是方案一、方案
二所无法企及的。从每天所得回报看,
在第1~3天,方案一最多;在第4天
方案一和方案二一样多,方案三最少;
在第5~8天,方案二最多;第9天开
始,方案三比其他两个方案所得回
报多得多,到第30天,所得回报已
超过2亿元。
我们看到,底数为2的指数函数模型比线性函数模型增长速度要快得多。
从中你对“指数爆涨”的含义有什么新的理解图3.2-1根据这里的分析,是否应该作出这样的选则:投资5天以下选方案一;投资5~8天选方案二;投资8天以上选方案三下面再看累计的回报数。通过计算器或计算机列表如下:因此,投资1~6天,应选择方案一;投资7天,应选择方案一或
方案二;投资8~10天,应选择方案二;投资11天(含11天)应
选择方案三.我们可以从上述的例子中体会到:
不同的增长模型,增长变化存在很大差异。分析例2某公司为了实现1000万元利润的目标,准备制定一个激励
销售人员的奖励方案:在销售利润达到10万元时,按销售利润
进行奖励,且奖金 (单位:万元)随销售利润 (单位:万元)
的增加而增加,但奖金总数不超过5万元,同时奖金不超过利润
的25%。现有三个奖励模型:
其中哪个模型能符合公司的要求?某个奖励模型符合公司要求,就是依据这个模型进行奖励时,
奖金总数不超过5万元,同时奖金不超过利润的25%,由于公
司总的利润目标为1000万元,所以人员销售利润一般不会超过
公司总的利润。于是,只需在区间[10,100]上,检验三个模型
是否符合公司要求即可。
不妨先作函数图象,通过观察函数的图象,得到初步的结论,
再通过具体计算,确认结果解:借助计算器或计算机作出函数
的图象(图3.2-2)观察图象发现,在区间[10,100]上,模型 的图象都有一部分在直线y=5的上方,只有模型
的图象始终在y=5的下方,这说明只有按模型
进行奖励时才符合公司的要求。下面通过计算确认上述判断.对于模型 ,它在[10,1000]上递增,而当时, ,因此当 时,首先计算哪个模型的奖金总数不超过5万所以该模型不符合要求;对于模型 由函数图象,并利用计算器,可知在区间(805,806)内有一个点 满足 ,由于它在区间[10,1000]上递增,因此当 时,所以该模型不符合要求;对于模型 ,它在区间[10,1000]上递增,而且当 时, ,所以它符合奖金总数不超过5万元的要求.再计算按模型 奖励时奖金是否不超过利润的25%,即当 时,是否有令利用计算器或计算机作出函数 的图象(图3.2-3),由图象可知它是递减的,因此综上所述,模型 确实能符合公司要求即所以当 时,说明按模型 奖励,奖金不会超过利润的25%练习1、四个变量 随变量 变化的数据如下表:关于 呈指数型函数变化的变量是2、某种计算机病毒是通过电子邮件进行传播的,如果某台计算机
感染上这种病毒,那么它就会在下一轮病毒发作时传播一次病毒,
并感染其他20台未感染病毒的计算机。现有10台计算即被第一轮
病毒感染,问被第五轮病毒感染的计算机共有多少台?我们知道,对于函数 ,指数函数
与幂函数 在区间 上都是增函数。从上述
两个例子可以看到,这三类函数的增长是有差异的。那么,这种差异的具体情况到底怎样呢?下面,我们不妨先以函数 为例进行研究利用计算器或计算机,列出自变量与函数值的对应值表(表3-5),
并在同一平面直角坐标系内画出三个函数的图象(表3.2-4)。可以
看到,虽然它们都是增函数,但它们的增长速度是不同的。表3-5观察请在图象上分别标出是不等式 成立的自变量
的取值范围表3-6表3-7探究结论:探究你能用同样的访法,讨论一下函数 ,
, 在区间 上的衰减情况吗?
在同一平面直角坐标系内作出下列函数图象,并比较它们的增长情况练习
