人教版数学八年级下册 《16.2 二次根式的乘除 第1课时》精品教学课件(共20张ppt)
文档属性
| 名称 | 人教版数学八年级下册 《16.2 二次根式的乘除 第1课时》精品教学课件(共20张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-21 13:23:34 | ||
图片预览








文档简介
(共20张PPT)
16.2 二次根式的乘除
第1课时
4.经历探究、归纳和应用等数学活动,培养由特殊到一般的
探究精神,提升逆向思维能力.
3.会用公式化简二次根式;
2.会进行二次根式的乘法运算;
1.探究二次根式的乘法法则和积的算术平方根的性质;
学习目标
二次根式
的乘除
(1)
难点
重点
巩固新知
课堂小结
布置作业
应用新知
创设情境
探究新知
复习引入
1.什么叫二次根式?二次根式有哪些性质?
2.二次根式的实质是什么?
形如 的式子叫做二次根式.
二次根式实质上是一个非负数的算术平方根.
二次根式有三个性质:
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
探究
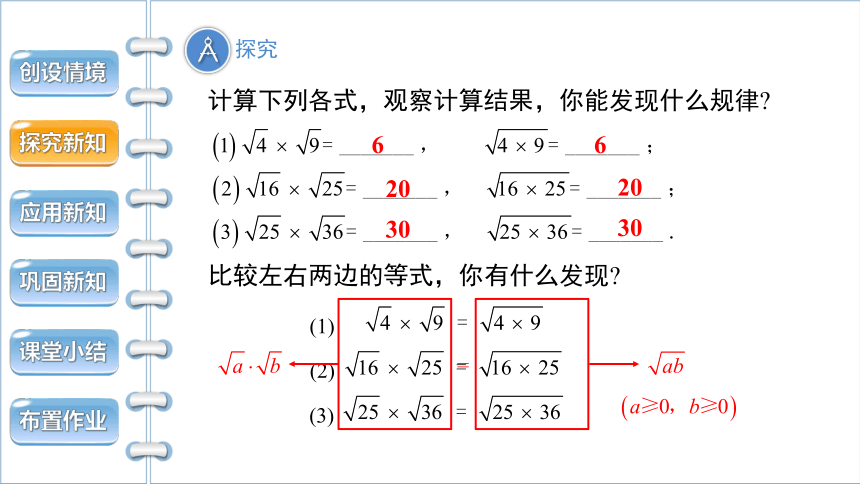
比较左右两边的等式,你有什么发现
计算下列各式,观察计算结果,你能发现什么规律
小组合作
1.独立思考,完成计算;
2.两人一组,讨论规律.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
探究
比较左右两边的等式,你有什么发现
6
6
20
20
30
30
计算下列各式,观察计算结果,你能发现什么规律
(1)
(2)
(3)
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
二次根式的乘法法则
一般地,二次根式的乘法法则是
两个非负数的算术平方根的积等于这两个数积的算术平方根.
数学语言
文字语言
归纳
巩固新知
课堂小结
布置作业
创设情境
解:
计算:
分析:直接利用 计算即可.
做一做
创设情境
探究新知
应用新知
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
二次根式的乘法法则
一般地,二次根式的乘法法则是
积的算术平方根等于积中各因式的算术平方根的积.
归纳
积的算术平方根的性质
反过来,可得积的算术平方根的性质
利用积的算术平方根的性质可以对二次根式化简.
巩固新知
课堂小结
布置作业
创设情境
解:
化简:
分析:直接利用 计算即可.
a
b
c
做一做
应用新知
探究新知
巩固新知
课堂小结
布置作业
创设情境
化简二次根式的基本要求
1.先把被开方数因数分解或者因式分解;
归纳
2.将能开得尽方的因数或因式开出来.
应用新知
探究新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
应用新知
【例1】计算:
解:
提示:
两个二次根式相乘,把被开方数相乘,根指数不变.即:
典型例题
巩固新知
课堂小结
布置作业
探究新知
创设情境
应用新知
【例2】化简:
解:
提示:
二次根式的乘法法则可以推广到多个二次根式进行相乘的运算.如:
典型例题
巩固新知
课堂小结
布置作业
创设情境
【例3】计算:
典型例题
探究新知
应用新知
巩固新知
课堂小结
布置作业
创设情境
【例3】计算:
典型例题
探究新知
应用新知
小结:
(1)二次根式相乘时,把被开方数和各个根号外面的系数分别相乘,将系数相乘的积作为积的系数,把被开方数相乘的积作为积的被开方数.
(2)在被开方数相乘时,可以先因数分解或因式分解.
1.判断下列各式是否正确,不正确的请予以改正:
应用新知
课堂小结
布置作业
创设情境
随堂练习
探究新知
巩固新知
解:(1)不正确,改正:
(2)不正确,改正:
应用新知
课堂小结
布置作业
创设情境
随堂练习
探究新知
巩固新知
2.一个长方形的长和宽分别是 和 .
求这个长方形的面积.
解:长方形的面积:
答:这个长方形的面积为 .
课堂小结
布置作业
探究新知
创设情境
3.计算:
练习
解:
随堂练习
应用新知
巩固新知
二次根式
的乘除
(1)
一般地,二次根式的乘法法则是
算术平方根的积等于被开方数的积的算术平方根.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
乘法法则
积的算术平方根
反过来,可得积的算术平方根的性质
积的算术平方根等于积中各因式的算术平方根的积.
化简要求
1. 先把被开方数因数分解或者因式分解;
2. 将能开得尽方的因数或因式开出来
布置作业
课本第10页
习题16.2:1,3.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
16.2 二次根式的乘除
第1课时
4.经历探究、归纳和应用等数学活动,培养由特殊到一般的
探究精神,提升逆向思维能力.
3.会用公式化简二次根式;
2.会进行二次根式的乘法运算;
1.探究二次根式的乘法法则和积的算术平方根的性质;
学习目标
二次根式
的乘除
(1)
难点
重点
巩固新知
课堂小结
布置作业
应用新知
创设情境
探究新知
复习引入
1.什么叫二次根式?二次根式有哪些性质?
2.二次根式的实质是什么?
形如 的式子叫做二次根式.
二次根式实质上是一个非负数的算术平方根.
二次根式有三个性质:
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
探究
比较左右两边的等式,你有什么发现
计算下列各式,观察计算结果,你能发现什么规律
小组合作
1.独立思考,完成计算;
2.两人一组,讨论规律.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
探究
比较左右两边的等式,你有什么发现
6
6
20
20
30
30
计算下列各式,观察计算结果,你能发现什么规律
(1)
(2)
(3)
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
二次根式的乘法法则
一般地,二次根式的乘法法则是
两个非负数的算术平方根的积等于这两个数积的算术平方根.
数学语言
文字语言
归纳
巩固新知
课堂小结
布置作业
创设情境
解:
计算:
分析:直接利用 计算即可.
做一做
创设情境
探究新知
应用新知
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
二次根式的乘法法则
一般地,二次根式的乘法法则是
积的算术平方根等于积中各因式的算术平方根的积.
归纳
积的算术平方根的性质
反过来,可得积的算术平方根的性质
利用积的算术平方根的性质可以对二次根式化简.
巩固新知
课堂小结
布置作业
创设情境
解:
化简:
分析:直接利用 计算即可.
a
b
c
做一做
应用新知
探究新知
巩固新知
课堂小结
布置作业
创设情境
化简二次根式的基本要求
1.先把被开方数因数分解或者因式分解;
归纳
2.将能开得尽方的因数或因式开出来.
应用新知
探究新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
应用新知
【例1】计算:
解:
提示:
两个二次根式相乘,把被开方数相乘,根指数不变.即:
典型例题
巩固新知
课堂小结
布置作业
探究新知
创设情境
应用新知
【例2】化简:
解:
提示:
二次根式的乘法法则可以推广到多个二次根式进行相乘的运算.如:
典型例题
巩固新知
课堂小结
布置作业
创设情境
【例3】计算:
典型例题
探究新知
应用新知
巩固新知
课堂小结
布置作业
创设情境
【例3】计算:
典型例题
探究新知
应用新知
小结:
(1)二次根式相乘时,把被开方数和各个根号外面的系数分别相乘,将系数相乘的积作为积的系数,把被开方数相乘的积作为积的被开方数.
(2)在被开方数相乘时,可以先因数分解或因式分解.
1.判断下列各式是否正确,不正确的请予以改正:
应用新知
课堂小结
布置作业
创设情境
随堂练习
探究新知
巩固新知
解:(1)不正确,改正:
(2)不正确,改正:
应用新知
课堂小结
布置作业
创设情境
随堂练习
探究新知
巩固新知
2.一个长方形的长和宽分别是 和 .
求这个长方形的面积.
解:长方形的面积:
答:这个长方形的面积为 .
课堂小结
布置作业
探究新知
创设情境
3.计算:
练习
解:
随堂练习
应用新知
巩固新知
二次根式
的乘除
(1)
一般地,二次根式的乘法法则是
算术平方根的积等于被开方数的积的算术平方根.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
乘法法则
积的算术平方根
反过来,可得积的算术平方根的性质
积的算术平方根等于积中各因式的算术平方根的积.
化简要求
1. 先把被开方数因数分解或者因式分解;
2. 将能开得尽方的因数或因式开出来
布置作业
课本第10页
习题16.2:1,3.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
