数学人教版八年级下册16.3 二次根式的加减 第1课时 教学课件(共17张ppt)
文档属性
| 名称 | 数学人教版八年级下册16.3 二次根式的加减 第1课时 教学课件(共17张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-21 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
16.3 二次根式的加减
第1课时
4.通过加减运算解决生活中的实际问题,体会数学知识应用的价值,提高学生学习数学的兴趣.
3.类比合并同类项的方法,探究归纳二次根式加减运算的方法;
2.会进行二次根式的加减运算;
1.掌握二次根式的加减运算的步骤和方法;
学习目标
二次根式
的加减(1)
重点
难点
巩固新知
课堂小结
布置作业
应用新知
创设情境
探究新知
复习引入
1.什么叫最简二次根式?
①被开方数不含分母;
②被开方数中不含能开得尽方的因数或因式.
这节课我们一起来研究这个问题.
二次根式的加减运算是怎样的呢?
2.你能将 化为最简二次根式吗?
3.化简后的二次根式可以进行加减运算吗?
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
探究
问题 现有一块长7.5 dm,宽5 dm的木板,能否采用如图的方式,在这块木板上截出两个面积分别是8 dm2和18 dm2的正方形木板?
5 dm
7.5 dm
小组合作
1.独立思考,计算求解;
2.两人一组,合作探究.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
(1)大、小正方形木板的边长分别为____dm和____ dm.
(2)从长方形木板上截取两个正方形木板,长方形木板够宽吗?
问题 现有一块长7.5 dm,宽5 dm的木板,能否采用如图的方式,在这块木板上截出两个面积分别是8 dm2和18 dm2的正方形木板?
5 dm
7.5 dm
问题 现有一块长7.5 dm,宽5 dm的木板,能否采用如图的方式,在这块木板上截出两个面积分别是8 dm2和18 dm2的正方形木板?
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
探究
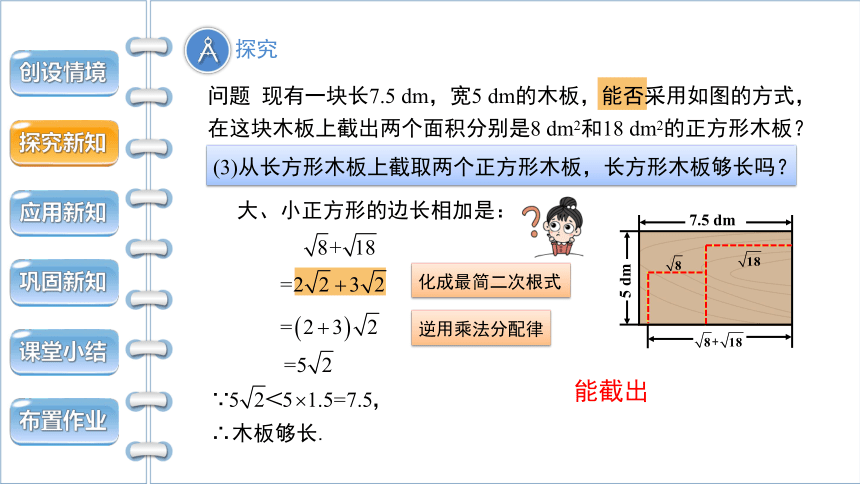
(3)从长方形木板上截取两个正方形木板,长方形木板够长吗?
5 dm
7.5 dm
能截出
化成最简二次根式
逆用乘法分配律
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
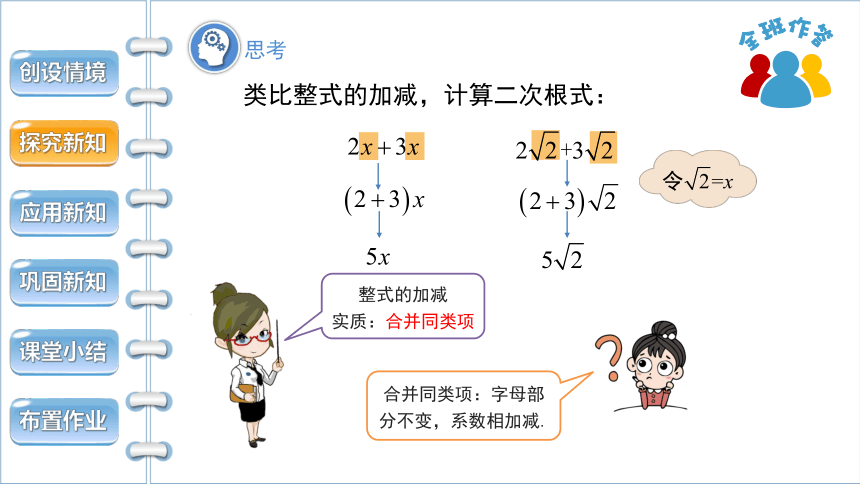
类比整式的加减,计算二次根式:
合并同类项:字母部分不变,系数相加减.
整式的加减
实质:合并同类项
思考
一般地,二次根式加减时,
可以先将二次根式化简成最简二次根式,
再将被开方数相同的二次根式进行合并.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
二次根式加减运算的法则
归纳
几个二次根式化成最简二次根式后,若被开方数相同,则这几个二次根式就是同类二次根式.
巩固新知
课堂小结
布置作业
创设情境
下列各组二次根式中是同类二次根式的是( )
做一做
创设情境
探究新知
应用新知
C
先化简成
最简二次根式.
巩固新知
课堂小结
布置作业
探究新知
创设情境
应用新知
典型例题
【例1】计算:
最简二次根式
同类二次根式
合并
一化,二找,三合并
巩固新知
课堂小结
布置作业
探究新知
创设情境
应用新知
典型例题
【例2】计算:
不能合并
1.下列计算是否正确?为什么?
应用新知
课堂小结
布置作业
创设情境
随堂练习
探究新知
巩固新知
一化,二找,三合并
应用新知
课堂小结
布置作业
创设情境
随堂练习
探究新知
巩固新知
2.计算:
应用新知
课堂小结
布置作业
创设情境
随堂练习
探究新知
巩固新知
3.计算:
二次根式
的加减
(1)
一般地,二次根式加减时,
可以先将二次根式化简成最简二次根式,
再将被开方数相同的二次根式进行合并.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
法则
步骤
一化,二找,三合并.
同类二次根式
几个二次根式化成最简二次根式后,若被开方数相同,则这几个二次根式就是同类二次根式.
布置作业
课本第15页
习题16.3:2,3.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
16.3 二次根式的加减
第1课时
4.通过加减运算解决生活中的实际问题,体会数学知识应用的价值,提高学生学习数学的兴趣.
3.类比合并同类项的方法,探究归纳二次根式加减运算的方法;
2.会进行二次根式的加减运算;
1.掌握二次根式的加减运算的步骤和方法;
学习目标
二次根式
的加减(1)
重点
难点
巩固新知
课堂小结
布置作业
应用新知
创设情境
探究新知
复习引入
1.什么叫最简二次根式?
①被开方数不含分母;
②被开方数中不含能开得尽方的因数或因式.
这节课我们一起来研究这个问题.
二次根式的加减运算是怎样的呢?
2.你能将 化为最简二次根式吗?
3.化简后的二次根式可以进行加减运算吗?
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
探究
问题 现有一块长7.5 dm,宽5 dm的木板,能否采用如图的方式,在这块木板上截出两个面积分别是8 dm2和18 dm2的正方形木板?
5 dm
7.5 dm
小组合作
1.独立思考,计算求解;
2.两人一组,合作探究.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
(1)大、小正方形木板的边长分别为____dm和____ dm.
(2)从长方形木板上截取两个正方形木板,长方形木板够宽吗?
问题 现有一块长7.5 dm,宽5 dm的木板,能否采用如图的方式,在这块木板上截出两个面积分别是8 dm2和18 dm2的正方形木板?
5 dm
7.5 dm
问题 现有一块长7.5 dm,宽5 dm的木板,能否采用如图的方式,在这块木板上截出两个面积分别是8 dm2和18 dm2的正方形木板?
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
探究
(3)从长方形木板上截取两个正方形木板,长方形木板够长吗?
5 dm
7.5 dm
能截出
化成最简二次根式
逆用乘法分配律
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
类比整式的加减,计算二次根式:
合并同类项:字母部分不变,系数相加减.
整式的加减
实质:合并同类项
思考
一般地,二次根式加减时,
可以先将二次根式化简成最简二次根式,
再将被开方数相同的二次根式进行合并.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
二次根式加减运算的法则
归纳
几个二次根式化成最简二次根式后,若被开方数相同,则这几个二次根式就是同类二次根式.
巩固新知
课堂小结
布置作业
创设情境
下列各组二次根式中是同类二次根式的是( )
做一做
创设情境
探究新知
应用新知
C
先化简成
最简二次根式.
巩固新知
课堂小结
布置作业
探究新知
创设情境
应用新知
典型例题
【例1】计算:
最简二次根式
同类二次根式
合并
一化,二找,三合并
巩固新知
课堂小结
布置作业
探究新知
创设情境
应用新知
典型例题
【例2】计算:
不能合并
1.下列计算是否正确?为什么?
应用新知
课堂小结
布置作业
创设情境
随堂练习
探究新知
巩固新知
一化,二找,三合并
应用新知
课堂小结
布置作业
创设情境
随堂练习
探究新知
巩固新知
2.计算:
应用新知
课堂小结
布置作业
创设情境
随堂练习
探究新知
巩固新知
3.计算:
二次根式
的加减
(1)
一般地,二次根式加减时,
可以先将二次根式化简成最简二次根式,
再将被开方数相同的二次根式进行合并.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
法则
步骤
一化,二找,三合并.
同类二次根式
几个二次根式化成最简二次根式后,若被开方数相同,则这几个二次根式就是同类二次根式.
布置作业
课本第15页
习题16.3:2,3.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
