数学人教版八年级下册19.1.1变量与函数 第1课时 精品教学课件(共20张ppt)
文档属性
| 名称 | 数学人教版八年级下册19.1.1变量与函数 第1课时 精品教学课件(共20张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-21 13:31:06 | ||
图片预览








文档简介
(共20张PPT)
第1课时
19.1.1 变量与函数
1.通过具体实例,让学生初步感知在具体情境中的变量与常量,能区分变量和常量.
2.经历观察、探究、分析的过程,发展合情推理和数学抽象的能力,清晰地表达两个变量之间的关系.
3.让学生参与变量的发现过程,强化数学应用意识,培养学生对学习的兴趣和积极参与数学活动的热情.
4.通过对具体实例的探究,认识数学来源于生活又反作用于实践.提高学生分析问题、解决问题的能力.
变量与函数
学习目标
乌鸦喝水涉及哪几个量?它们之间有什么不同呢?
思考
水量
石子数量
水面高度
水面高度,石子数量在
水量固定
改变
不变
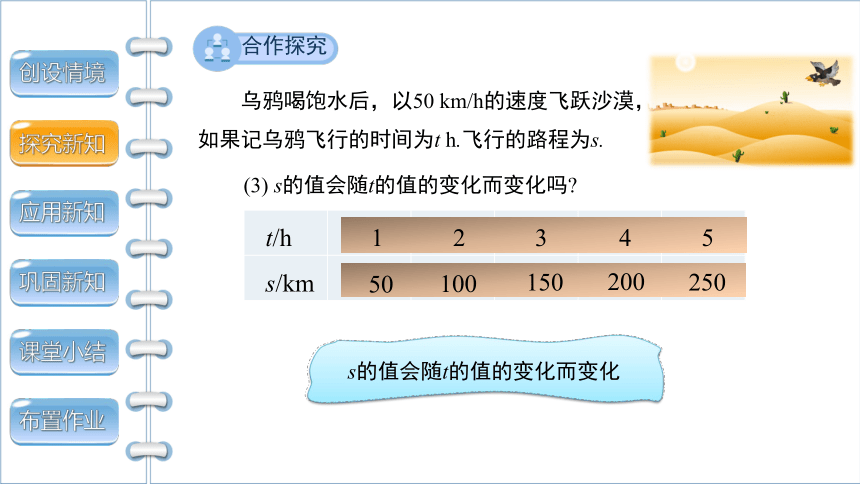
乌鸦喝饱水后,以50 km/h的速度飞跃沙漠,如果记乌鸦飞行的时间为t h.飞行的路程为s.
(1)请填写下表:
t/h 1 2 3 4 5
s/km
50
100
150
200
250
合作探究
合作探究
乌鸦喝饱水后,以50 km/h的速度飞跃沙漠,如果记乌鸦飞行的时间为t h.飞行的路程为s.
(2)在上述问题中涉及哪几个量?这几个量之间有什么不同呢?
乌鸦飞行的速度
乌鸦飞行的路程
乌鸦飞行的时间
不变的量
变化的量
t/h
s/km
50
100
150
200
250
乌鸦喝饱水后,以50 km/h的速度飞跃沙漠,如果记乌鸦飞行的时间为t h.飞行的路程为s.
(3) s的值会随t的值的变化而变化吗
s的值会随t的值的变化而变化
1
2
3
4
5
合作探究
合作探究
假设乌鸦每捕获一只昆虫需要20秒,请回答下列问题:
(1)乌鸦捕获2只,4只,6只,8只,10只昆虫时,分别用时多久呢?
昆虫数(只) 2 4 6 8 10
用时(秒)
80
120
160
40
200
(2)在上述问题中,涉及到了哪几个量呢?它们之间有什么不同呢?
乌鸦捕获一只昆虫的时间
乌鸦捕获昆虫的数量
乌鸦捕获昆虫的总时
不变的量
变化的量
x 2 4 6 8 10
t
(3)乌鸦捕获了x只昆虫,用时t秒, t会随x的变化而怎样变化呢?
80
120
160
40
200
捕获的昆虫越多,用时越长.t会随x的增大而增大.
上面这些问题中涉及到的量,你会怎样分类呢
乌鸦飞行的速度
乌鸦飞行的路程
乌鸦飞行的时间
不变的量
变化的量
乌鸦捕获一只昆虫的时间
乌鸦捕获昆虫的数量
乌鸦捕获昆虫的总时
在某个变化过程中,我们称数值发生变化的量为变量;数值始终不变的量叫做常量.
变量和常量
判断常量和变量的方法:
(1)看它是否在同一个变化过程中;
(2)看它在这个变化过程中的取值是否改变.
你知道如何判断常量和变量吗?
典型例题
【例1】电影票的售价为10元/张,第一场售出150张票,第二场售出205张票,第三场售出310张票. 设一场电影售出x张票,票房收入为y元.
(1)三场电影的票房收入各是多少元
(2)请指出上述问题中的变量和常量.
(3)y的值随x的值的变化而变化吗
解:(1)第一场电影的票房收入为150×10=1500(元).
第二场电影的票房收入为205×10=2050(元).
第三场电影的票房收入为310×10=3100(元).
x 150 205 310
y 1500 2050 3100
典型例题
【例1】电影票的售价为10元/张,第一场售出150张票,第二场售出205张票,第三场售出310张票. 设一场电影售出x张票,票房收入为y元.
(1)三场电影的票房收入各是多少元
(2)请指出上述问题中的变量和常量.
(3)y的值随x的值的变化而变化吗
(2)变量为:售票的张数x、票房收入y;
常量为:一张电影票的售价
(3) y的值随x的值的变化而变化.
x 150 205 310
y 1500 2050 3100
典型例题
【例2】你见过水中涟漪吗 如图所示,圆形水波慢慢的扩大.
(1)当圆的半径r分别为10 cm,20 cm,30 cm时,圆的面积S分别为多少 请填表回答;
半径r(cm) 10 20 30
圆面积S(cm2)
(2)请指出上述问题中的变量和常量.
(3)S的值会随r的值的变化而怎样变化
解:(2)变量为:圆的半径r,圆的面积S;常量为:圆周率π.
(3)圆的半径越大,面积就越大.S的值随r的值的增大而增大.
100π
400π
900π
S πr2
1.指出下列变化过程中的变量和常量:
(1)汽油的价格是8.5 元/升,加油x升,车主加油付油费y元;
(2)小明看一本200页的小说,看完这本小说需要t天,平均每天所看的页数为n;
(3)用长为30 cm的绳子围矩形,围成的矩形一边长为x cm,其面积为S.
随堂练习
解:(1)变量x,y;常量8.5.
(2)变量t,n;常量200.
(3)变量x,S;常量30.
2.汽车以60 km/h的速度匀速行驶,行驶路程为s km,行驶时间为t h,
(1)填写下表:
随堂练习
(2)请指出上述问题中的变量和常量.
(3)s的值随t的值的变化而怎样变化?
t/h 1 2 3 4 5
s/km
60
120
180
240
300
解:(2)变量s,t;常量60.
(3) s的值随t的值的增大而增大.
3.用10 m长的绳子围一个矩形.当矩形的一边长x分别为3 m,3.5 m,4 m,4.5 m时,它的邻边长y分别为多少?y的值随x的值的变化而变化吗?
随堂练习
解:当x 3 m时,y 5 3=2(m) ;
当x 3.5 m时,y 5 3.5=1.5(m) ;
当x 4 m时,y 5 4=1(m) ;
当x 4.5 m时,y 5 4.5=0.5(m).
y的值随x的值的变化而变化.
判断变量和常量的方法
①看它是否在同一个变化过程中;
②看它在这个变化过程中的取值是否改变.
变量与函数
定义
在某个变化过程中,我们称数值发生变化的量为变量;数值始终不变的量叫做常量.
教科书第71-72页
(1)-(4)
再见
第1课时
19.1.1 变量与函数
1.通过具体实例,让学生初步感知在具体情境中的变量与常量,能区分变量和常量.
2.经历观察、探究、分析的过程,发展合情推理和数学抽象的能力,清晰地表达两个变量之间的关系.
3.让学生参与变量的发现过程,强化数学应用意识,培养学生对学习的兴趣和积极参与数学活动的热情.
4.通过对具体实例的探究,认识数学来源于生活又反作用于实践.提高学生分析问题、解决问题的能力.
变量与函数
学习目标
乌鸦喝水涉及哪几个量?它们之间有什么不同呢?
思考
水量
石子数量
水面高度
水面高度,石子数量在
水量固定
改变
不变
乌鸦喝饱水后,以50 km/h的速度飞跃沙漠,如果记乌鸦飞行的时间为t h.飞行的路程为s.
(1)请填写下表:
t/h 1 2 3 4 5
s/km
50
100
150
200
250
合作探究
合作探究
乌鸦喝饱水后,以50 km/h的速度飞跃沙漠,如果记乌鸦飞行的时间为t h.飞行的路程为s.
(2)在上述问题中涉及哪几个量?这几个量之间有什么不同呢?
乌鸦飞行的速度
乌鸦飞行的路程
乌鸦飞行的时间
不变的量
变化的量
t/h
s/km
50
100
150
200
250
乌鸦喝饱水后,以50 km/h的速度飞跃沙漠,如果记乌鸦飞行的时间为t h.飞行的路程为s.
(3) s的值会随t的值的变化而变化吗
s的值会随t的值的变化而变化
1
2
3
4
5
合作探究
合作探究
假设乌鸦每捕获一只昆虫需要20秒,请回答下列问题:
(1)乌鸦捕获2只,4只,6只,8只,10只昆虫时,分别用时多久呢?
昆虫数(只) 2 4 6 8 10
用时(秒)
80
120
160
40
200
(2)在上述问题中,涉及到了哪几个量呢?它们之间有什么不同呢?
乌鸦捕获一只昆虫的时间
乌鸦捕获昆虫的数量
乌鸦捕获昆虫的总时
不变的量
变化的量
x 2 4 6 8 10
t
(3)乌鸦捕获了x只昆虫,用时t秒, t会随x的变化而怎样变化呢?
80
120
160
40
200
捕获的昆虫越多,用时越长.t会随x的增大而增大.
上面这些问题中涉及到的量,你会怎样分类呢
乌鸦飞行的速度
乌鸦飞行的路程
乌鸦飞行的时间
不变的量
变化的量
乌鸦捕获一只昆虫的时间
乌鸦捕获昆虫的数量
乌鸦捕获昆虫的总时
在某个变化过程中,我们称数值发生变化的量为变量;数值始终不变的量叫做常量.
变量和常量
判断常量和变量的方法:
(1)看它是否在同一个变化过程中;
(2)看它在这个变化过程中的取值是否改变.
你知道如何判断常量和变量吗?
典型例题
【例1】电影票的售价为10元/张,第一场售出150张票,第二场售出205张票,第三场售出310张票. 设一场电影售出x张票,票房收入为y元.
(1)三场电影的票房收入各是多少元
(2)请指出上述问题中的变量和常量.
(3)y的值随x的值的变化而变化吗
解:(1)第一场电影的票房收入为150×10=1500(元).
第二场电影的票房收入为205×10=2050(元).
第三场电影的票房收入为310×10=3100(元).
x 150 205 310
y 1500 2050 3100
典型例题
【例1】电影票的售价为10元/张,第一场售出150张票,第二场售出205张票,第三场售出310张票. 设一场电影售出x张票,票房收入为y元.
(1)三场电影的票房收入各是多少元
(2)请指出上述问题中的变量和常量.
(3)y的值随x的值的变化而变化吗
(2)变量为:售票的张数x、票房收入y;
常量为:一张电影票的售价
(3) y的值随x的值的变化而变化.
x 150 205 310
y 1500 2050 3100
典型例题
【例2】你见过水中涟漪吗 如图所示,圆形水波慢慢的扩大.
(1)当圆的半径r分别为10 cm,20 cm,30 cm时,圆的面积S分别为多少 请填表回答;
半径r(cm) 10 20 30
圆面积S(cm2)
(2)请指出上述问题中的变量和常量.
(3)S的值会随r的值的变化而怎样变化
解:(2)变量为:圆的半径r,圆的面积S;常量为:圆周率π.
(3)圆的半径越大,面积就越大.S的值随r的值的增大而增大.
100π
400π
900π
S πr2
1.指出下列变化过程中的变量和常量:
(1)汽油的价格是8.5 元/升,加油x升,车主加油付油费y元;
(2)小明看一本200页的小说,看完这本小说需要t天,平均每天所看的页数为n;
(3)用长为30 cm的绳子围矩形,围成的矩形一边长为x cm,其面积为S.
随堂练习
解:(1)变量x,y;常量8.5.
(2)变量t,n;常量200.
(3)变量x,S;常量30.
2.汽车以60 km/h的速度匀速行驶,行驶路程为s km,行驶时间为t h,
(1)填写下表:
随堂练习
(2)请指出上述问题中的变量和常量.
(3)s的值随t的值的变化而怎样变化?
t/h 1 2 3 4 5
s/km
60
120
180
240
300
解:(2)变量s,t;常量60.
(3) s的值随t的值的增大而增大.
3.用10 m长的绳子围一个矩形.当矩形的一边长x分别为3 m,3.5 m,4 m,4.5 m时,它的邻边长y分别为多少?y的值随x的值的变化而变化吗?
随堂练习
解:当x 3 m时,y 5 3=2(m) ;
当x 3.5 m时,y 5 3.5=1.5(m) ;
当x 4 m时,y 5 4=1(m) ;
当x 4.5 m时,y 5 4.5=0.5(m).
y的值随x的值的变化而变化.
判断变量和常量的方法
①看它是否在同一个变化过程中;
②看它在这个变化过程中的取值是否改变.
变量与函数
定义
在某个变化过程中,我们称数值发生变化的量为变量;数值始终不变的量叫做常量.
教科书第71-72页
(1)-(4)
再见
