数学人教版八年级下册 《第1课时 矩形的性质》教学课件(共21张ppt)
文档属性
| 名称 | 数学人教版八年级下册 《第1课时 矩形的性质》教学课件(共21张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 289.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-21 00:00:00 | ||
图片预览




文档简介
(共21张PPT)
第十八章 平行四边形
18.2 特殊平行四边形
第1课时 矩形的性质
学习目标
1. 理解矩形的概念,了解它与平行四边形之间的关系.
2. 经历矩形性质定理的探索过程,进一步发展合情推理能力.
3.能够用综合法证明矩形的性质定理以及其他相关结论,进一步发展演绎推理能力.
4.探索并掌握直角三角形的性质定理.
1.什么叫平行四边形?
2.平行四边形有哪些性质?
①边:
②角:
③对角线:
A
B
C
D
对边平行且相等.
对角相等且邻角互补.
互相平分.
两组对边分别平行的四边形叫做平行四边形 .
复习回顾
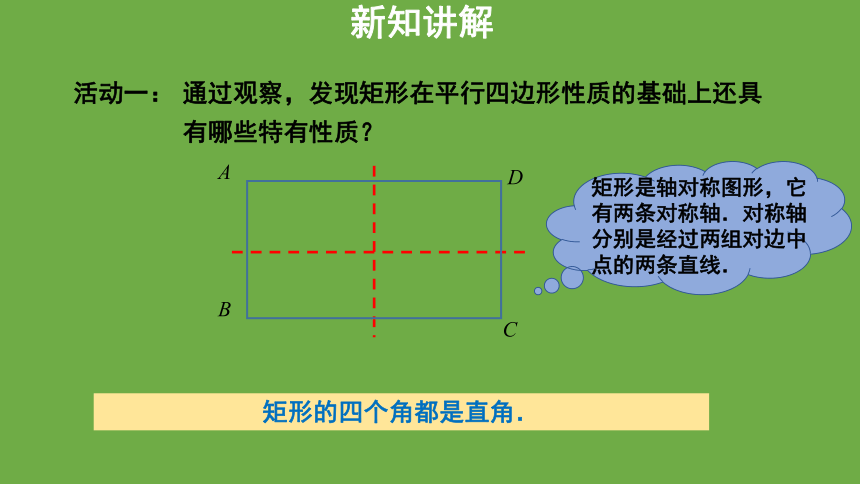
活动一:
通过观察,发现矩形在平行四边形性质的基础上还具有哪些特有性质?
矩形的四个角都是直角.
矩形是轴对称图形,它有两条对称轴.对称轴分别是经过两组对边中点的两条直线.
新知讲解
A
D
C
B
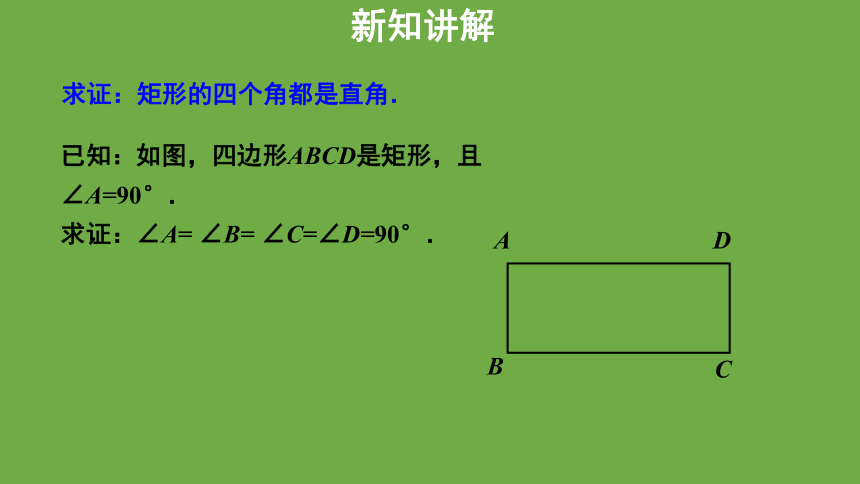
求证:矩形的四个角都是直角.
A
B
C
D
已知:如图,四边形ABCD是矩形,且∠A=90°.
求证:∠A= ∠B= ∠C=∠D=90°.
新知讲解
证明:∵四边形ABCD是矩形,
∴ ∠C=∠A=90°,∠D=∠B,AD∥BC.
∴ ∠A+ ∠B=180°,
∴ ∠D=∠B=180°-∠A
=180°- 90°=90°,
即矩形的四个角都是直角.
A
B
C
D
新知讲解
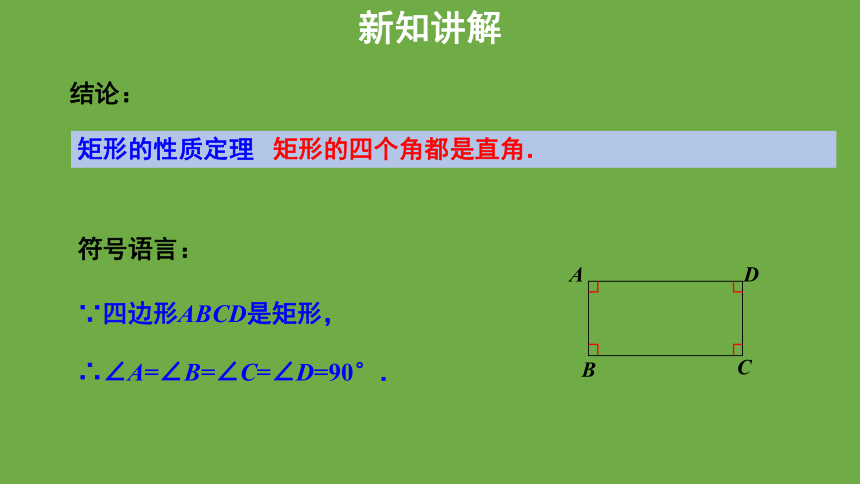
结论:
矩形的性质定理 矩形的四个角都是直角.
A
B
C
D
符号语言:
∵四边形ABCD是矩形,
∴∠A=∠B=∠C=∠D=90°.
新知讲解
活动二:
观察图形的变化,你发现了什么?
矩形的对角线相等.
新知讲解
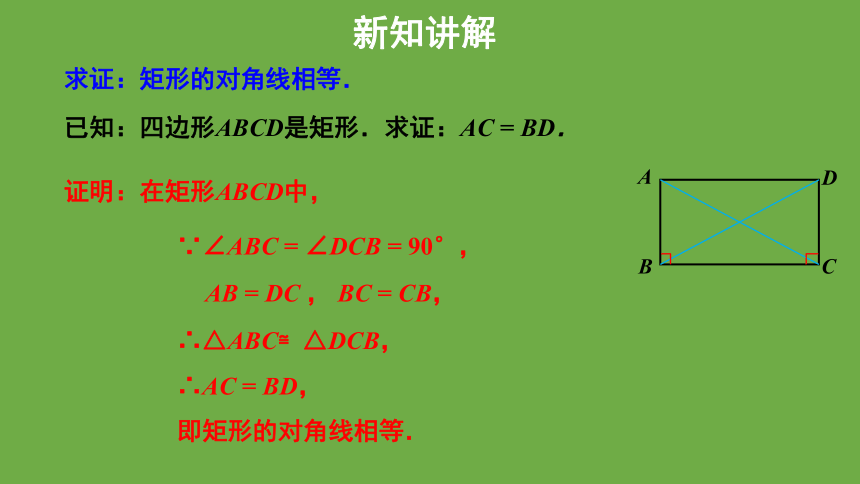
求证:矩形的对角线相等.
已知:四边形ABCD是矩形.求证:AC = BD.
A
B
C
D
证明:在矩形ABCD中,
∵∠ABC = ∠DCB = 90°,
AB = DC , BC = CB,
∴△ABC≌△DCB,
∴AC = BD,
即矩形的对角线相等.
新知讲解
结论:
矩形的性质定理 矩形的对角线相等.
A
B
C
D
符号语言:
∵四边形ABCD是矩形,
∴AC = BD.
新知讲解
O
C
B
A
D
证明:延长BO至D, 使OD=BO,连接AD、DC.
∵AO=OC, BO=OD,
∴四边形ABCD是平行四边形.
∵∠ABC=90°,
∴平行四边形ABCD是矩形,
∴AC=BD,
例:已知:在Rt△ABC中,∠ABC=90°,BO是AC上的中线.
求证: BO = AC.
∴BO= BD= AC.
典型例题
直角三角形的性质定理
直角三角形斜边上的中线等于斜边的一半.
C
B
A
O
符号语言:
Rt△ABC中,
∵∠ABC=90°,OA=OC,
∴BO= AC.
典型例题
1.如图,矩形ABCD的两条对角线相交于点O,已知∠BOC=120°,AB=6cm. 求AC的长.
A
B
C
D
O
随堂练习
解:∵四边形ABCD是矩形,
∴AC=BD,AC=2AO,BD=2BO,
∴AO=BO.
∵∠BOC=120°,∴∠AOB=60°,
∴△ABO为等边三角形.
∴AO=AB=6cm,
∴AC=2AB=12cm.
A
B
C
D
O
随堂练习
2.已知: 如图, 过矩形ABCD的顶点作CE//BD,交AB的延长线于E . 求证:∠CAE=∠CEA.
O
A
B
C
D
E
证明:∵四边形ABCD是矩形,
∴AC=BD,CD∥AB.
∵CE∥BD,
∴四边形DBEC是平行四边形.
∴CE=BD,∴AC=CE.
∴ ∠CAE=∠CEA.
随堂练习
3.在 ABCD中,点E在边CD的延长线上,且AE//BD,EF⊥BC,交BC的延长线于点F.
求证:DF= CE.
A
B
C
D
E
F
随堂练习
证明:∵四边形ABCD是平行四边形,
∴AB=CD , AB∥CD.
又 ∵AE∥BD,
∴四边形ABDE是平行四边形,
∴DE=AB,∴CD=DE.
又∵EF⊥BC于F,
∴在Rt△CEF中得, DF=CE.
A
B
C
D
E
F
随堂练习
矩形的概念:
有一个角是直角的平行四边形叫做矩形.
矩形的性质:
矩形的性质定理1:矩形的四个角都是直角.
矩形的性质定理2:矩形的对角线相等.
课堂小结
直角三角形的性质定理2:
直角三角形斜边上的中线等于斜边的一半.
拓展素材
拓展素材
再见
第十八章 平行四边形
18.2 特殊平行四边形
第1课时 矩形的性质
学习目标
1. 理解矩形的概念,了解它与平行四边形之间的关系.
2. 经历矩形性质定理的探索过程,进一步发展合情推理能力.
3.能够用综合法证明矩形的性质定理以及其他相关结论,进一步发展演绎推理能力.
4.探索并掌握直角三角形的性质定理.
1.什么叫平行四边形?
2.平行四边形有哪些性质?
①边:
②角:
③对角线:
A
B
C
D
对边平行且相等.
对角相等且邻角互补.
互相平分.
两组对边分别平行的四边形叫做平行四边形 .
复习回顾
活动一:
通过观察,发现矩形在平行四边形性质的基础上还具有哪些特有性质?
矩形的四个角都是直角.
矩形是轴对称图形,它有两条对称轴.对称轴分别是经过两组对边中点的两条直线.
新知讲解
A
D
C
B
求证:矩形的四个角都是直角.
A
B
C
D
已知:如图,四边形ABCD是矩形,且∠A=90°.
求证:∠A= ∠B= ∠C=∠D=90°.
新知讲解
证明:∵四边形ABCD是矩形,
∴ ∠C=∠A=90°,∠D=∠B,AD∥BC.
∴ ∠A+ ∠B=180°,
∴ ∠D=∠B=180°-∠A
=180°- 90°=90°,
即矩形的四个角都是直角.
A
B
C
D
新知讲解
结论:
矩形的性质定理 矩形的四个角都是直角.
A
B
C
D
符号语言:
∵四边形ABCD是矩形,
∴∠A=∠B=∠C=∠D=90°.
新知讲解
活动二:
观察图形的变化,你发现了什么?
矩形的对角线相等.
新知讲解
求证:矩形的对角线相等.
已知:四边形ABCD是矩形.求证:AC = BD.
A
B
C
D
证明:在矩形ABCD中,
∵∠ABC = ∠DCB = 90°,
AB = DC , BC = CB,
∴△ABC≌△DCB,
∴AC = BD,
即矩形的对角线相等.
新知讲解
结论:
矩形的性质定理 矩形的对角线相等.
A
B
C
D
符号语言:
∵四边形ABCD是矩形,
∴AC = BD.
新知讲解
O
C
B
A
D
证明:延长BO至D, 使OD=BO,连接AD、DC.
∵AO=OC, BO=OD,
∴四边形ABCD是平行四边形.
∵∠ABC=90°,
∴平行四边形ABCD是矩形,
∴AC=BD,
例:已知:在Rt△ABC中,∠ABC=90°,BO是AC上的中线.
求证: BO = AC.
∴BO= BD= AC.
典型例题
直角三角形的性质定理
直角三角形斜边上的中线等于斜边的一半.
C
B
A
O
符号语言:
Rt△ABC中,
∵∠ABC=90°,OA=OC,
∴BO= AC.
典型例题
1.如图,矩形ABCD的两条对角线相交于点O,已知∠BOC=120°,AB=6cm. 求AC的长.
A
B
C
D
O
随堂练习
解:∵四边形ABCD是矩形,
∴AC=BD,AC=2AO,BD=2BO,
∴AO=BO.
∵∠BOC=120°,∴∠AOB=60°,
∴△ABO为等边三角形.
∴AO=AB=6cm,
∴AC=2AB=12cm.
A
B
C
D
O
随堂练习
2.已知: 如图, 过矩形ABCD的顶点作CE//BD,交AB的延长线于E . 求证:∠CAE=∠CEA.
O
A
B
C
D
E
证明:∵四边形ABCD是矩形,
∴AC=BD,CD∥AB.
∵CE∥BD,
∴四边形DBEC是平行四边形.
∴CE=BD,∴AC=CE.
∴ ∠CAE=∠CEA.
随堂练习
3.在 ABCD中,点E在边CD的延长线上,且AE//BD,EF⊥BC,交BC的延长线于点F.
求证:DF= CE.
A
B
C
D
E
F
随堂练习
证明:∵四边形ABCD是平行四边形,
∴AB=CD , AB∥CD.
又 ∵AE∥BD,
∴四边形ABDE是平行四边形,
∴DE=AB,∴CD=DE.
又∵EF⊥BC于F,
∴在Rt△CEF中得, DF=CE.
A
B
C
D
E
F
随堂练习
矩形的概念:
有一个角是直角的平行四边形叫做矩形.
矩形的性质:
矩形的性质定理1:矩形的四个角都是直角.
矩形的性质定理2:矩形的对角线相等.
课堂小结
直角三角形的性质定理2:
直角三角形斜边上的中线等于斜边的一半.
拓展素材
拓展素材
再见
