数学人教版八年级下册18.1.1 第1课时 平行四边形的性质 教学课件(共21张PPT)
文档属性
| 名称 | 数学人教版八年级下册18.1.1 第1课时 平行四边形的性质 教学课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 487.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-21 00:00:00 | ||
图片预览





文档简介
(共21张PPT)
第十八章 平行四边形
第1课时 平行四边形的性质(1)
18.1 平行四边形
学习目标
1.理解并掌握平行四边形的概念和平行四边形对边、对角相等的性质.
2.会用平行四边形的性质解决简单的平行四边形的计算问题,并会进行有关的论证.
3.初步体会几何研究的一般思路与方法.
情境导入
我们一起来观察下面的几个图形,想一想它们是什么几何图形的形象?
平行四边形
探究新知
平行四边形是我们常见的图形,你还能举出平行四边形在生活中应用的例子吗?
几何语言:
因为四边形ABCD是平行四边形
所以四边形ABCD是平行四边形
AB∥CD,
AD∥BC
所以
AB∥CD,
AD∥BC
因为
A
D
B
C
探究新知
两组对边分别平行的四边形叫做平行四边形.
表示:如图,在四边形ABCD中,AB//DC,AD//BC,那么四边形ABCD是平行四边形.
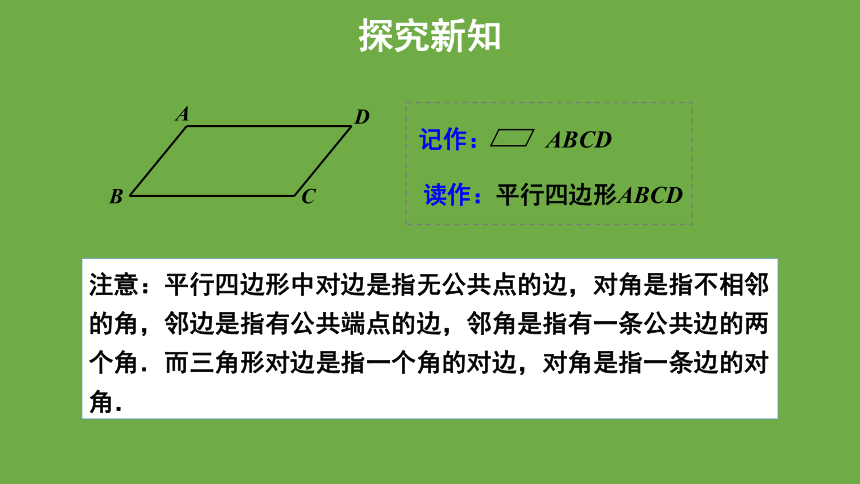
读作:平行四边形ABCD
A
D
B
C
记作: ABCD
探究新知
注意:平行四边形中对边是指无公共点的边,对角是指不相邻的角,邻边是指有公共端点的边,邻角是指有一条公共边的两个角.而三角形对边是指一个角的对边,对角是指一条边的对角.
A
B
C
D
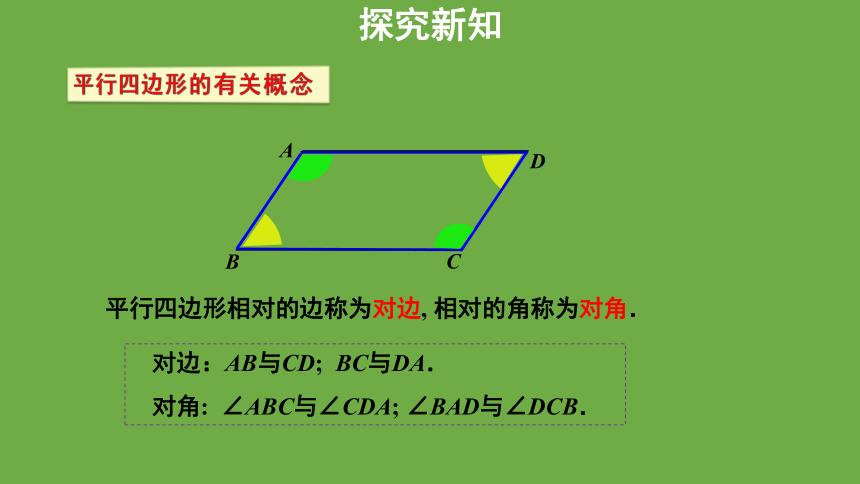
平行四边形相对的边称为对边, 相对的角称为对角.
对边:AB与CD; BC与DA.
对角: ∠ABC与∠CDA; ∠BAD与∠DCB.
平行四边形的有关概念
探究新知
探究新知
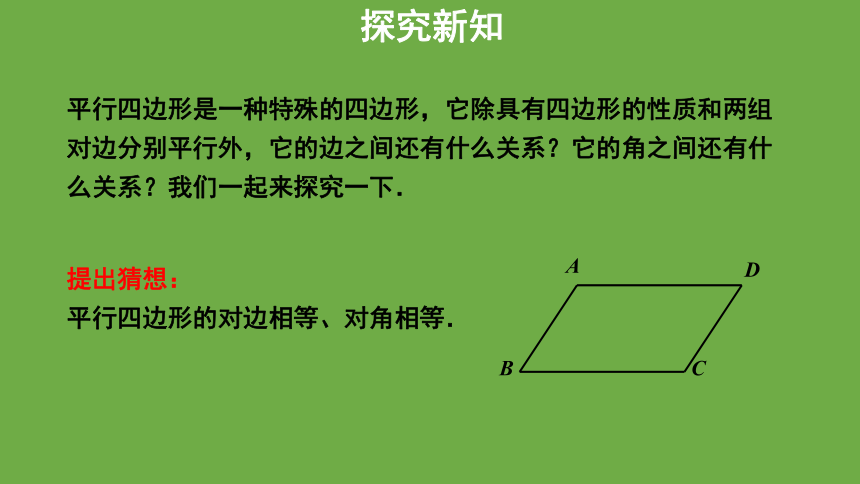
平行四边形是一种特殊的四边形,它除具有四边形的性质和两组对边分别平行外,它的边之间还有什么关系?它的角之间还有什么关系?我们一起来探究一下.
提出猜想:
平行四边形的对边相等、对角相等.
A
D
B
C
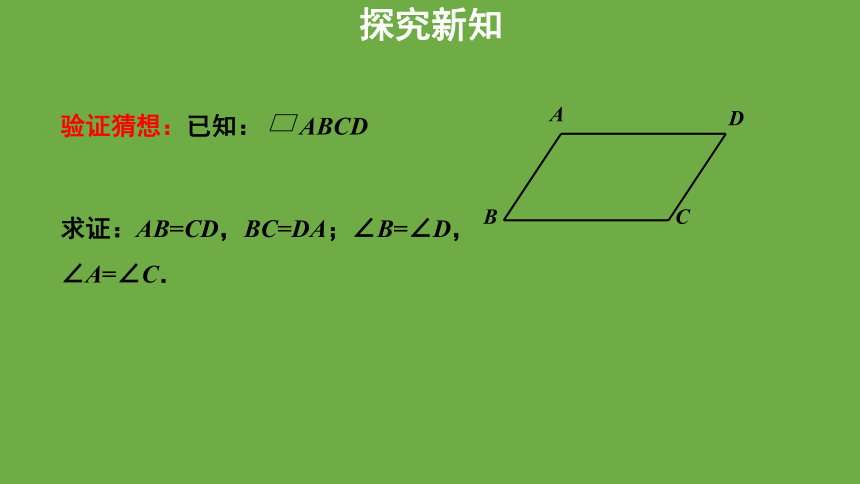
验证猜想:已知: ABCD
求证:AB=CD,BC=DA;∠B=∠D,∠A=∠C.
A
D
B
C
探究新知
探究新知
即∠BAD=∠DCB.
因为四边形ABCD是平行四边形,所以AB∥CD,AD∥BC.
所以∠1=∠2,∠3=∠4.
∠1=∠2,
AC=CA,
∠3=∠4,
所以 △ABC≌△CDA(ASA),
所以AB=CD,BC=DA,∠B=∠D
又∠1=∠2,∠4=∠3,
所以∠1+∠4=∠2+∠3,
在△ABC和△CDA中,
证明:连接AC.
A
D
B
C
1
2
4
3
几何语言:
因为四边形ABCD是平行四边形,
所以AB=CD,AD=BC.
性质定理1:平行四边形的对边相等.
性质定理2:平行四边形的对角相等.
因为四边形ABCD是平行四边形,
所以∠A=∠C,∠B=∠D.
几何语言:
A
D
B
C
平行四边形的性质定理
探究新知
A
B
C
D
E
F
例1 如图,在 ABCD中,DE⊥AB,BF ⊥CD,垂足分别为E、F.求证: AE=CF.
证明:
因为 四边形ABCD是平行四边形,
所以∠A=∠C,AD=CB.
又∠AED=∠CFB=90°,
所以 △ ADE≌ △ CBF.
所以 AE=CF.
应用新知
例2 求证:(1)夹在两平行直线间的平行线段相等.
(2)如果两条直线平行,那么一条直线上各点到另一条直线的距离相等.
(1)已知:如图,直线EF∥MN,A,D是直线EF上的任意两点,过点 A,D 作AB∥CD, 分别交MN于点B, C.
求证:AB=CD.
E
F
M
N
应用新知
证明:因为 AD∥BC,AB∥CD,
所以四边形ABCD是平行四边形,
所以AB=CD.
E
F
M
N
应用新知
已知:如图,EF∥MN,A,D是直线 EF上的任意两点,AB⊥MN,垂足是B,DC⊥MN,垂足是C. 求证:AB=CD.
(2)求证:如果两条直线平行,那么一条直线上各点到另一条直线的距离相等.
E
F
M
N
证明:因为 AB⊥MN,DC⊥MN,
所以四边形ABCD是平行四边形,所以AB=CD.
所以AB∥CD.
因为EF∥MN,所以AD∥BC.
应用新知
两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.
B
A
a
b
如图,直线a∥b,A是直线a上的任意一点,AB ⊥b ,B是垂足,线段AB的长就是a、b之间的距离.
两条平行线之间的距离
应用新知
1.如图,在
若∠A=130°,则∠B=______ 、∠C=______ 、∠D=______.
ABCD中,
A:基础知识:
B:变式训练:
(1)若∠A+ ∠C= 200°,则∠A=______ 、∠B=______;
(2)若∠A:∠B= 5:4,则∠C=______ 、∠D=______.
50°
130°
50°
100°
80°
100°
80°
A
D
B
C
随堂检测
C:拓展延伸:
(1)∠A:∠B : ∠C : ∠D的度数可能是( )
A. 1 : 2 : 3 : 4 B.3 : 2 : 3 : 2
C.2 : 3 : 3 : 2 D.2 : 2 : 3 : 3
(2)连接AC, 若∠D=60°, ∠DAC=40°,则 ∠B=____, ∠BAC=____.
B
60°
80°
A
D
B
C
如图,在
ABCD中,
随堂检测
随堂检测
2.如图,△ABC是等腰三角形,P是底边BC上一动点,且PE//AB,PF//AC.求证:PE+PF=AB.
证明:因为PE//AB,PF//AC,
所以四边形AEPF为平行四边形,∠C=∠FPB.
所以PE=AF.
因为△ABC是等腰三角形,
所以∠B=∠C.所以∠B=∠FPB.
所以PF=BF.所以PE+PF=AF+BF=AB.
本节课主要学习了哪些知识
1.本节课研究了什么图形的性质?
2.什么是平行四边形?
3.平行四边形有哪些性质?
性质定理1:平行四边形的对边相等.
性质定理2:平行四边形的对角相等.
4.什么是两条平行线之间的距离?
课堂小结
再见
第十八章 平行四边形
第1课时 平行四边形的性质(1)
18.1 平行四边形
学习目标
1.理解并掌握平行四边形的概念和平行四边形对边、对角相等的性质.
2.会用平行四边形的性质解决简单的平行四边形的计算问题,并会进行有关的论证.
3.初步体会几何研究的一般思路与方法.
情境导入
我们一起来观察下面的几个图形,想一想它们是什么几何图形的形象?
平行四边形
探究新知
平行四边形是我们常见的图形,你还能举出平行四边形在生活中应用的例子吗?
几何语言:
因为四边形ABCD是平行四边形
所以四边形ABCD是平行四边形
AB∥CD,
AD∥BC
所以
AB∥CD,
AD∥BC
因为
A
D
B
C
探究新知
两组对边分别平行的四边形叫做平行四边形.
表示:如图,在四边形ABCD中,AB//DC,AD//BC,那么四边形ABCD是平行四边形.
读作:平行四边形ABCD
A
D
B
C
记作: ABCD
探究新知
注意:平行四边形中对边是指无公共点的边,对角是指不相邻的角,邻边是指有公共端点的边,邻角是指有一条公共边的两个角.而三角形对边是指一个角的对边,对角是指一条边的对角.
A
B
C
D
平行四边形相对的边称为对边, 相对的角称为对角.
对边:AB与CD; BC与DA.
对角: ∠ABC与∠CDA; ∠BAD与∠DCB.
平行四边形的有关概念
探究新知
探究新知
平行四边形是一种特殊的四边形,它除具有四边形的性质和两组对边分别平行外,它的边之间还有什么关系?它的角之间还有什么关系?我们一起来探究一下.
提出猜想:
平行四边形的对边相等、对角相等.
A
D
B
C
验证猜想:已知: ABCD
求证:AB=CD,BC=DA;∠B=∠D,∠A=∠C.
A
D
B
C
探究新知
探究新知
即∠BAD=∠DCB.
因为四边形ABCD是平行四边形,所以AB∥CD,AD∥BC.
所以∠1=∠2,∠3=∠4.
∠1=∠2,
AC=CA,
∠3=∠4,
所以 △ABC≌△CDA(ASA),
所以AB=CD,BC=DA,∠B=∠D
又∠1=∠2,∠4=∠3,
所以∠1+∠4=∠2+∠3,
在△ABC和△CDA中,
证明:连接AC.
A
D
B
C
1
2
4
3
几何语言:
因为四边形ABCD是平行四边形,
所以AB=CD,AD=BC.
性质定理1:平行四边形的对边相等.
性质定理2:平行四边形的对角相等.
因为四边形ABCD是平行四边形,
所以∠A=∠C,∠B=∠D.
几何语言:
A
D
B
C
平行四边形的性质定理
探究新知
A
B
C
D
E
F
例1 如图,在 ABCD中,DE⊥AB,BF ⊥CD,垂足分别为E、F.求证: AE=CF.
证明:
因为 四边形ABCD是平行四边形,
所以∠A=∠C,AD=CB.
又∠AED=∠CFB=90°,
所以 △ ADE≌ △ CBF.
所以 AE=CF.
应用新知
例2 求证:(1)夹在两平行直线间的平行线段相等.
(2)如果两条直线平行,那么一条直线上各点到另一条直线的距离相等.
(1)已知:如图,直线EF∥MN,A,D是直线EF上的任意两点,过点 A,D 作AB∥CD, 分别交MN于点B, C.
求证:AB=CD.
E
F
M
N
应用新知
证明:因为 AD∥BC,AB∥CD,
所以四边形ABCD是平行四边形,
所以AB=CD.
E
F
M
N
应用新知
已知:如图,EF∥MN,A,D是直线 EF上的任意两点,AB⊥MN,垂足是B,DC⊥MN,垂足是C. 求证:AB=CD.
(2)求证:如果两条直线平行,那么一条直线上各点到另一条直线的距离相等.
E
F
M
N
证明:因为 AB⊥MN,DC⊥MN,
所以四边形ABCD是平行四边形,所以AB=CD.
所以AB∥CD.
因为EF∥MN,所以AD∥BC.
应用新知
两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.
B
A
a
b
如图,直线a∥b,A是直线a上的任意一点,AB ⊥b ,B是垂足,线段AB的长就是a、b之间的距离.
两条平行线之间的距离
应用新知
1.如图,在
若∠A=130°,则∠B=______ 、∠C=______ 、∠D=______.
ABCD中,
A:基础知识:
B:变式训练:
(1)若∠A+ ∠C= 200°,则∠A=______ 、∠B=______;
(2)若∠A:∠B= 5:4,则∠C=______ 、∠D=______.
50°
130°
50°
100°
80°
100°
80°
A
D
B
C
随堂检测
C:拓展延伸:
(1)∠A:∠B : ∠C : ∠D的度数可能是( )
A. 1 : 2 : 3 : 4 B.3 : 2 : 3 : 2
C.2 : 3 : 3 : 2 D.2 : 2 : 3 : 3
(2)连接AC, 若∠D=60°, ∠DAC=40°,则 ∠B=____, ∠BAC=____.
B
60°
80°
A
D
B
C
如图,在
ABCD中,
随堂检测
随堂检测
2.如图,△ABC是等腰三角形,P是底边BC上一动点,且PE//AB,PF//AC.求证:PE+PF=AB.
证明:因为PE//AB,PF//AC,
所以四边形AEPF为平行四边形,∠C=∠FPB.
所以PE=AF.
因为△ABC是等腰三角形,
所以∠B=∠C.所以∠B=∠FPB.
所以PF=BF.所以PE+PF=AF+BF=AB.
本节课主要学习了哪些知识
1.本节课研究了什么图形的性质?
2.什么是平行四边形?
3.平行四边形有哪些性质?
性质定理1:平行四边形的对边相等.
性质定理2:平行四边形的对角相等.
4.什么是两条平行线之间的距离?
课堂小结
再见
