三角形的内角和课件(共18张PPT) 人教版四年级下册数学
文档属性
| 名称 | 三角形的内角和课件(共18张PPT) 人教版四年级下册数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-20 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
三角形的内角和
什么是三角形的内角?
一个三角形中,里面的三个角就是它的内角
复习旧知,提出猜想
你知道三角形的内角和指的是什么吗
三角形的内角和是三个内角度数相加的和。
复习旧知,提出猜想
(90°)
(90°)
(45°)
(60°)
(30°)
(45°)
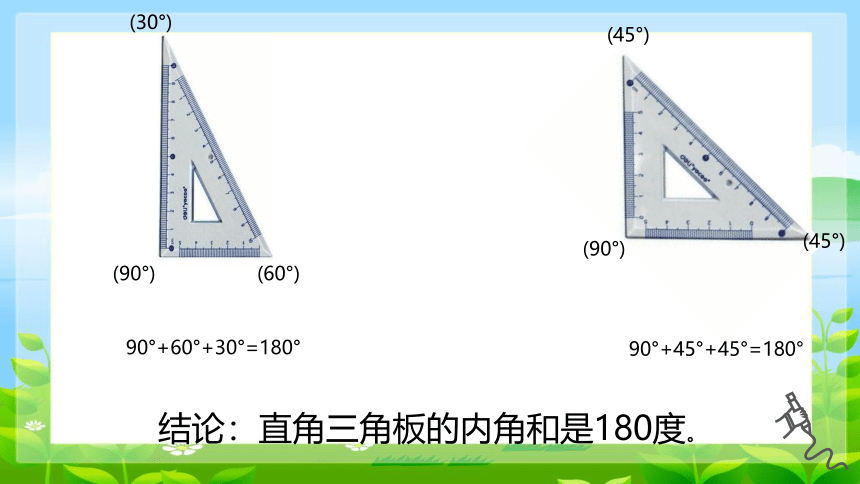
90°+60°+30°=180°
结论:直角三角板的内角和是180度。
90°+45°+45°=180°
大小、形状不同的三角形,它都是180°吗?它们的内角和一样吗?
大胆猜想:三角形的内角和是180°
复习旧知,提出猜想
2
1
3
∠1+∠2+∠3= 84°+58°+38°=180°
∠1=84°
∠2=58°
∠3=38°
三角形的内角和是180度。
验证一 测量法:量一量,三角形三个内角分别是多少?内
角和是多少?展示你们的答案,说说你发现了什么?
操作实验,验证猜想
验证二 折拼法 :按照下面的方法折一折,你发现了什么?
1
2
2
3
3
钝角三角形
1
∠1+∠2+∠3
=
平角
=180°
三角形的内角和是180度。
操作实验,验证猜想
2
1
1
3
3
锐角三角形
2
三角形的内角和是180度。
∠1+∠2+∠3
=
平角
=180°
操作实验,验证猜想
1
1
2
2
3
3
直角三角形
三角形的内角和是180度。
∠1+∠2+∠3
=
平角
=180°
操作实验,验证猜想
3
3
2
1
三角形的内角和是180度。
∠1+∠2+∠3
=
平角
=180°
验证三 撕拼法:将三角形三个内角分别剪下来拼在一起,
你发现了什么?(注:剪之前标注好要拼的角哦!)
操作实验,验证猜想
2
1
现在我们告诉这三兄弟他们的内角和是……
一样大,都是180°
结论:
归纳总结,反思释疑
任意三角形的内角和都是180°。
游戏:找朋友
每组卡片中,哪三个角可以组成一个三角形?
60°+30°+90°=180°
54°+46°+80°=180°
巩固新知,拓展练习
真相大白
(被挡住的角是多少度?)
180°-90°-60°=30°
90°-35°=55°
180°-45°-20°=115°
180°-(75+28°)=77°
巩固新知,拓展练习
已知等腰三角形的风筝,一个底角70°,顶角多少度?
方法一: 180°-70°-70°=40°
70°
70°
?
方法二: 180°-70°×2=40°
答:顶角是40°。
巩固新知,拓展练习
这节课你们都学会了哪些知识?
三角形的内角和是180度。
三角形的内角和
有多种方法可以求证三角形的内角和:
测量法
折拼法
撕拼法
全课小结,感受文化
帕斯卡与“三角形内角和”的故事
帕斯卡(1623-1662)是法国著名的数学家、物理学家、哲学家和散文家。早在300多年前,12岁的帕斯卡就独自发现了任何三角形的内角和都是180°。
全课小结,感受文化
谢 谢 !
三角形的内角和
什么是三角形的内角?
一个三角形中,里面的三个角就是它的内角
复习旧知,提出猜想
你知道三角形的内角和指的是什么吗
三角形的内角和是三个内角度数相加的和。
复习旧知,提出猜想
(90°)
(90°)
(45°)
(60°)
(30°)
(45°)
90°+60°+30°=180°
结论:直角三角板的内角和是180度。
90°+45°+45°=180°
大小、形状不同的三角形,它都是180°吗?它们的内角和一样吗?
大胆猜想:三角形的内角和是180°
复习旧知,提出猜想
2
1
3
∠1+∠2+∠3= 84°+58°+38°=180°
∠1=84°
∠2=58°
∠3=38°
三角形的内角和是180度。
验证一 测量法:量一量,三角形三个内角分别是多少?内
角和是多少?展示你们的答案,说说你发现了什么?
操作实验,验证猜想
验证二 折拼法 :按照下面的方法折一折,你发现了什么?
1
2
2
3
3
钝角三角形
1
∠1+∠2+∠3
=
平角
=180°
三角形的内角和是180度。
操作实验,验证猜想
2
1
1
3
3
锐角三角形
2
三角形的内角和是180度。
∠1+∠2+∠3
=
平角
=180°
操作实验,验证猜想
1
1
2
2
3
3
直角三角形
三角形的内角和是180度。
∠1+∠2+∠3
=
平角
=180°
操作实验,验证猜想
3
3
2
1
三角形的内角和是180度。
∠1+∠2+∠3
=
平角
=180°
验证三 撕拼法:将三角形三个内角分别剪下来拼在一起,
你发现了什么?(注:剪之前标注好要拼的角哦!)
操作实验,验证猜想
2
1
现在我们告诉这三兄弟他们的内角和是……
一样大,都是180°
结论:
归纳总结,反思释疑
任意三角形的内角和都是180°。
游戏:找朋友
每组卡片中,哪三个角可以组成一个三角形?
60°+30°+90°=180°
54°+46°+80°=180°
巩固新知,拓展练习
真相大白
(被挡住的角是多少度?)
180°-90°-60°=30°
90°-35°=55°
180°-45°-20°=115°
180°-(75+28°)=77°
巩固新知,拓展练习
已知等腰三角形的风筝,一个底角70°,顶角多少度?
方法一: 180°-70°-70°=40°
70°
70°
?
方法二: 180°-70°×2=40°
答:顶角是40°。
巩固新知,拓展练习
这节课你们都学会了哪些知识?
三角形的内角和是180度。
三角形的内角和
有多种方法可以求证三角形的内角和:
测量法
折拼法
撕拼法
全课小结,感受文化
帕斯卡与“三角形内角和”的故事
帕斯卡(1623-1662)是法国著名的数学家、物理学家、哲学家和散文家。早在300多年前,12岁的帕斯卡就独自发现了任何三角形的内角和都是180°。
全课小结,感受文化
谢 谢 !
