垂直于直径的弦(1)(浙江省台州市玉环县)
文档属性
| 名称 | 垂直于直径的弦(1)(浙江省台州市玉环县) |
|
|
| 格式 | rar | ||
| 文件大小 | 884.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-17 21:54:00 | ||
图片预览



文档简介
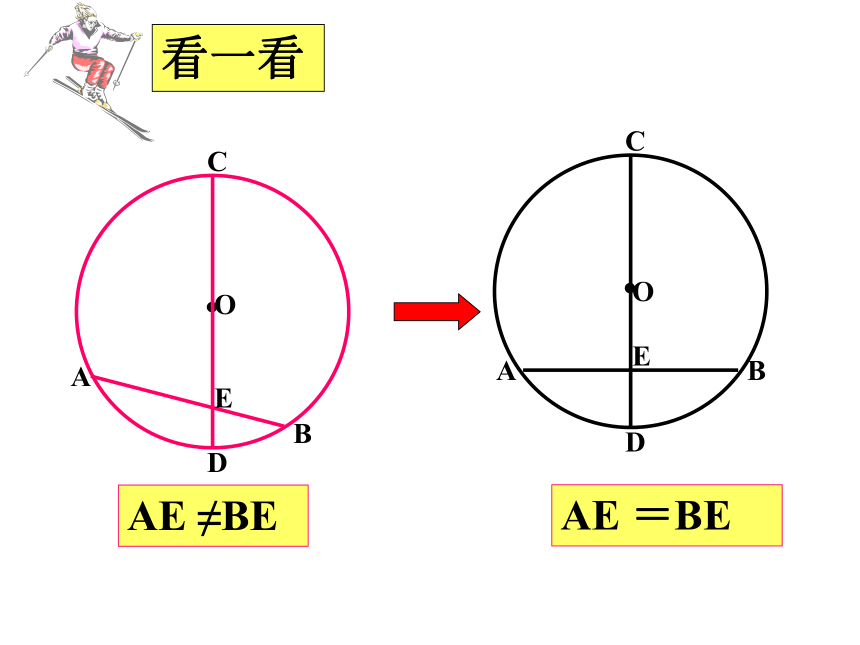
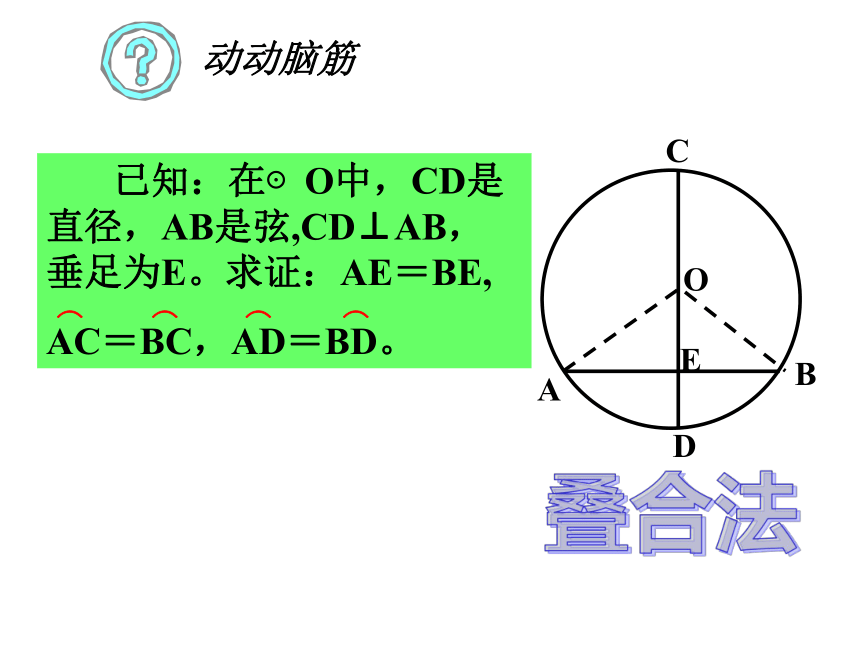
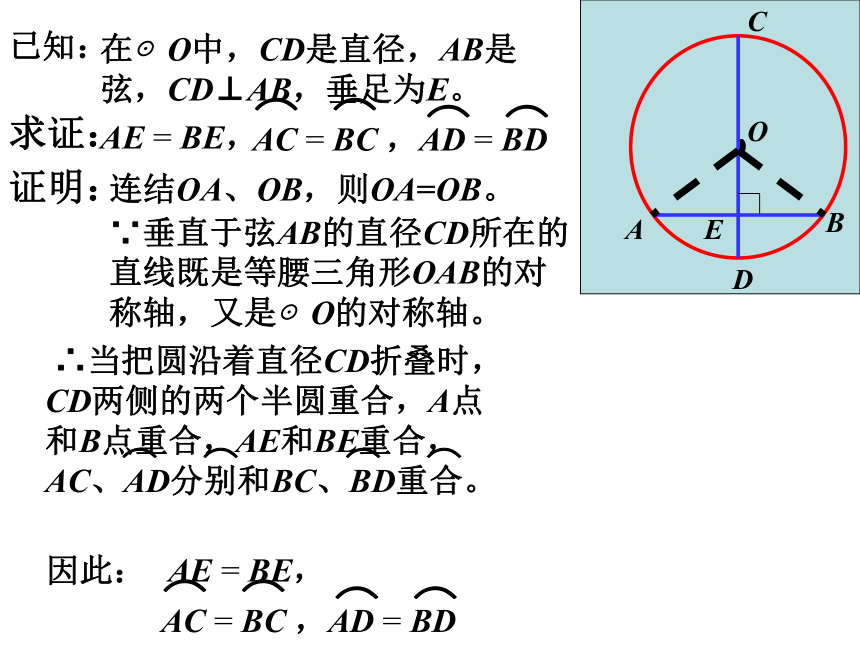
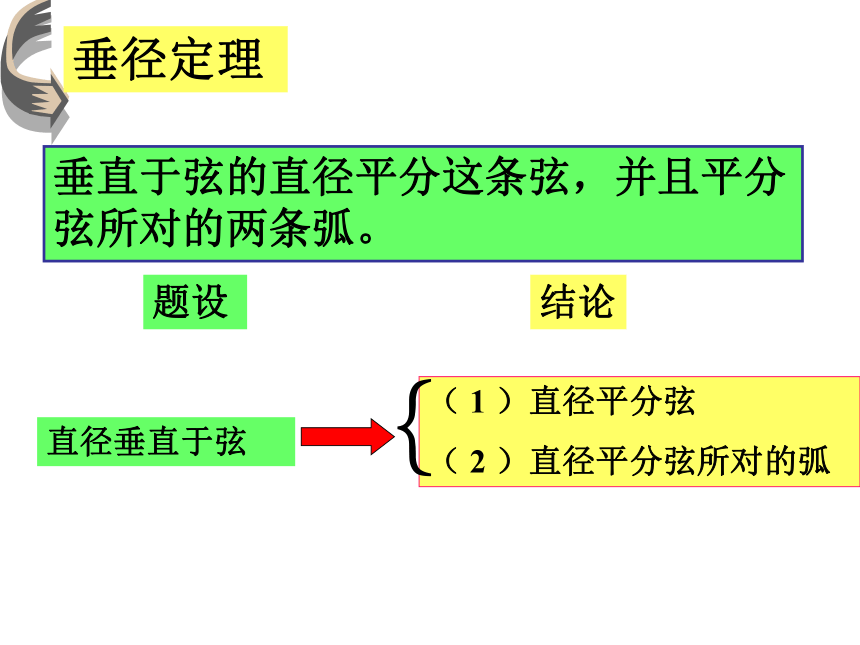
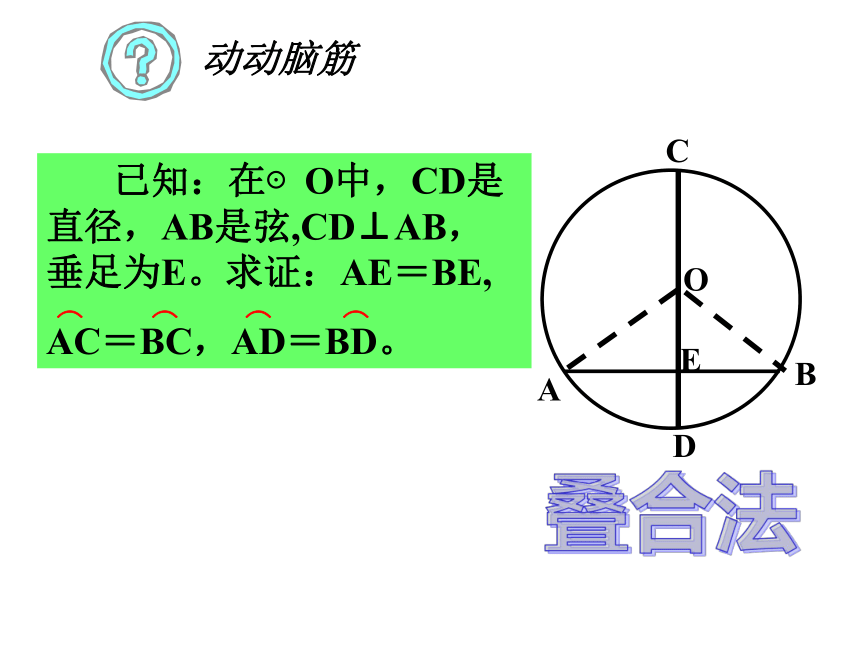
课件26张PPT。24.1.2垂直于弦的直径1 、什么是轴对称图形?我们学过哪些轴对称图形?如果一个图形沿一条直线对折,直线两旁的部分能够互相重合,那么这个图形叫轴对称图形如线段、角、等腰三角形、矩形、菱形、等腰梯形、正方形。2 、我们所学的圆是不是轴对称图形呢?圆是轴对称图形,经过圆心的每一条直线都是它们的对称轴AE ≠BEAE =BE叠合法AE = BE,求证:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为E。已知:证明:连结OA、OB,则OA=OB。∵垂直于弦AB的直径CD所在的直线既是等腰三角形OAB的对称轴,又是⊙O的对称轴。 ∴当把圆沿着直径CD折叠时,CD两侧的两个半圆重合,A点和B点重合,AE和BE重合,AC、AD分别和BC、BD重合。因此:AE = BE,垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。题设结论直径垂直于弦( 1 )直径平分弦
( 2 )直径平分弦所对的弧{叠合法叠合法平分弦 (不是直径) 的直径垂直于弦,并且平分弦所对的两条弧。题设结论直径平分弦
(不是直径)( 1 )直径垂直于弦
( 2 )直径平分弦所对的弧{叠合法直径平分一条弦所对的弧,则直径垂直平分这条弦。题设结论直径平分弦所对的弧
( 1 )直径垂直于弦
( 2 )直径平分弦{直径垂直于弦直径平分弦
(不是直径)直径平分弦
所对的弧( 1 )垂直于弦的直线平分弦,并且平分弦所对的弧…………………………………………( 2 )弦所对的两弧中点的连线,垂直于弦,并且经过圆心……………………………………( 3 )圆的不与直径垂直的弦必不被这条直径平分…………………………………………( 4 )平分弦的直径垂直于弦,并且平分弦所对的两条弧………………………………………( 5 )圆内两条非直径的弦不能互相平分()×√××√三 概括性质1。直径垂直于弦直径平分弦所对的弧直径平分弦2.分一条弧成相等的两条弧的点,
叫做这条弧的中点。
∵CD为直径,CD⊥ AB (或 OC ⊥ AB )
E1.连结 AB2.作 AB 的垂直平分线,作法:例 2 如图,已知在⊙ O 中,弦 AB 的长为 8 厘米,圆心 O 到 AB 的距离为 3 厘米,求⊙ O 的半径。解:连结 OA 过 O 作 OE ⊥ AB ,垂足为 E ,则 OE = 3 厘米, AE =是。∵ AB = 8 厘米∴ AE = 4 厘米。
在 RtAOE 中,根据勾股定理有 OA = 5 厘米∴⊙ O 的半径为 5 厘米。例 3 已知:如图,在以 O 为圆心的两个同心圆中,大圆的弦 AB 交小圆于 C , D 两点。
求证: AC = BD 。证明:过 O 作 OE ⊥ AB ,垂足为 E ,则 AE =是, CE = DE 。
AE - CE =是- DE 。
所以, AC = BDEABCDO1、如图1,在⊙O中, AB是 弦, OC = OD。
求证:AC = BD (1)ABCDO2、如图2,在⊙O中, CD是
弦, OA = OB。
求证:AC = BD (2)EE例 4 已知:⊙ O 中弦 AB ∥CD。
求证: AC = BD⌒⌒圆的两条平行弦所夹的弧相等挑战自我在⊙O弦AB//CD,AB=6,CD=8, ⊙O的半径为5
求:AB,CD之间的距离挑战自我如图,⊙O 与矩形 ABCD 交于 E , F ,G ,H , AH=4, HG=6,BE=2
求:EF。MN462已知:AB是⊙O直径,CD
是弦,AE⊥CD,BF⊥CD
求证:EC=DFH小结: 解决有关弦的问题,经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件。请同学们谈谈你的收获-------
( 2 )直径平分弦所对的弧{叠合法叠合法平分弦 (不是直径) 的直径垂直于弦,并且平分弦所对的两条弧。题设结论直径平分弦
(不是直径)( 1 )直径垂直于弦
( 2 )直径平分弦所对的弧{叠合法直径平分一条弦所对的弧,则直径垂直平分这条弦。题设结论直径平分弦所对的弧
( 1 )直径垂直于弦
( 2 )直径平分弦{直径垂直于弦直径平分弦
(不是直径)直径平分弦
所对的弧( 1 )垂直于弦的直线平分弦,并且平分弦所对的弧…………………………………………( 2 )弦所对的两弧中点的连线,垂直于弦,并且经过圆心……………………………………( 3 )圆的不与直径垂直的弦必不被这条直径平分…………………………………………( 4 )平分弦的直径垂直于弦,并且平分弦所对的两条弧………………………………………( 5 )圆内两条非直径的弦不能互相平分()×√××√三 概括性质1。直径垂直于弦直径平分弦所对的弧直径平分弦2.分一条弧成相等的两条弧的点,
叫做这条弧的中点。
∵CD为直径,CD⊥ AB (或 OC ⊥ AB )
E1.连结 AB2.作 AB 的垂直平分线,作法:例 2 如图,已知在⊙ O 中,弦 AB 的长为 8 厘米,圆心 O 到 AB 的距离为 3 厘米,求⊙ O 的半径。解:连结 OA 过 O 作 OE ⊥ AB ,垂足为 E ,则 OE = 3 厘米, AE =是。∵ AB = 8 厘米∴ AE = 4 厘米。
在 RtAOE 中,根据勾股定理有 OA = 5 厘米∴⊙ O 的半径为 5 厘米。例 3 已知:如图,在以 O 为圆心的两个同心圆中,大圆的弦 AB 交小圆于 C , D 两点。
求证: AC = BD 。证明:过 O 作 OE ⊥ AB ,垂足为 E ,则 AE =是, CE = DE 。
AE - CE =是- DE 。
所以, AC = BDEABCDO1、如图1,在⊙O中, AB是 弦, OC = OD。
求证:AC = BD (1)ABCDO2、如图2,在⊙O中, CD是
弦, OA = OB。
求证:AC = BD (2)EE例 4 已知:⊙ O 中弦 AB ∥CD。
求证: AC = BD⌒⌒圆的两条平行弦所夹的弧相等挑战自我在⊙O弦AB//CD,AB=6,CD=8, ⊙O的半径为5
求:AB,CD之间的距离挑战自我如图,⊙O 与矩形 ABCD 交于 E , F ,G ,H , AH=4, HG=6,BE=2
求:EF。MN462已知:AB是⊙O直径,CD
是弦,AE⊥CD,BF⊥CD
求证:EC=DFH小结: 解决有关弦的问题,经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件。请同学们谈谈你的收获-------
同课章节目录
