人教版数学八年级上册 13.3等腰三角形第1课时等腰三角形课件(共18张PPT)
文档属性
| 名称 | 人教版数学八年级上册 13.3等腰三角形第1课时等腰三角形课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 516.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-21 16:10:34 | ||
图片预览


文档简介
(共18张PPT)
13.3 等腰三角形
第1课时 等腰三角形
新课导入
A
B
C
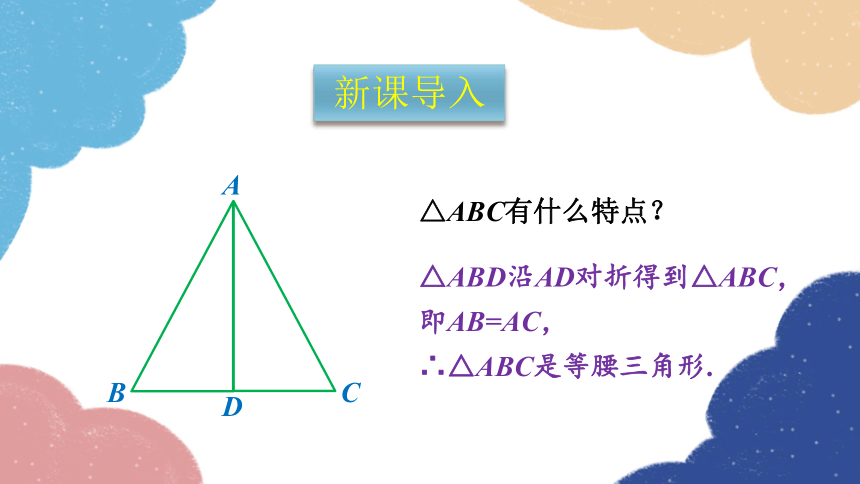
△ABC有什么特点?
△ABD沿AD对折得到△ABC,
即AB=AC,
∴△ABC是等腰三角形.
D
A
B
C
D
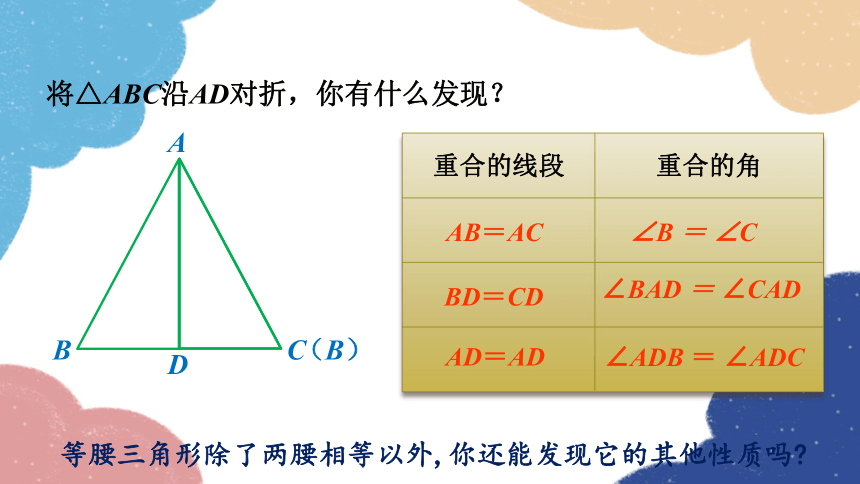
将△ABC沿AD对折,你有什么发现?
(B)
重合的线段 重合的角
AB=AC
BD=CD
AD=AD
∠B = ∠C
∠BAD = ∠CAD
∠ADB = ∠ADC
等腰三角形除了两腰相等以外,你还能发现它的其他性质吗
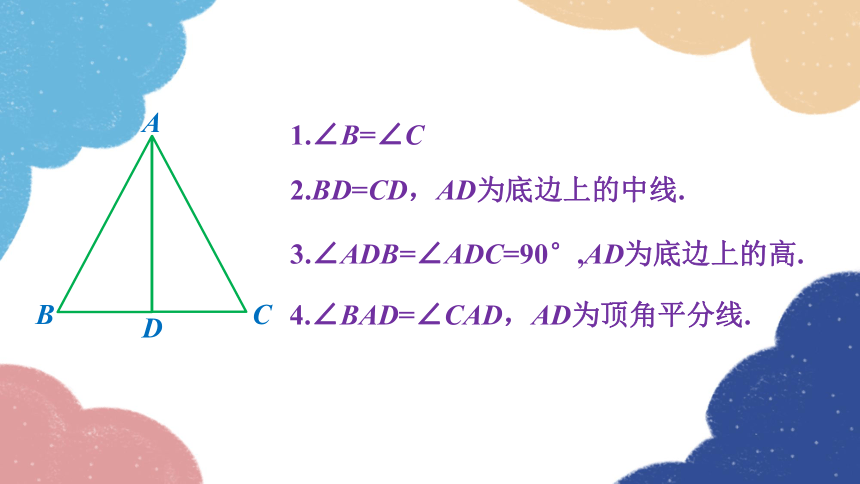
1.∠B=∠C
2.BD=CD,AD为底边上的中线.
3.∠ADB=∠ADC=90°,AD为底边上的高.
4.∠BAD=∠CAD,AD为顶角平分线.
A
B
C
D
等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合(简写成“三线合一”)
问题2:结论2、3、4可以用一句话归纳吗?
问题1:结论1用文字如何表述?
等腰三角形的两个底角相等(简写“等边对等角”)
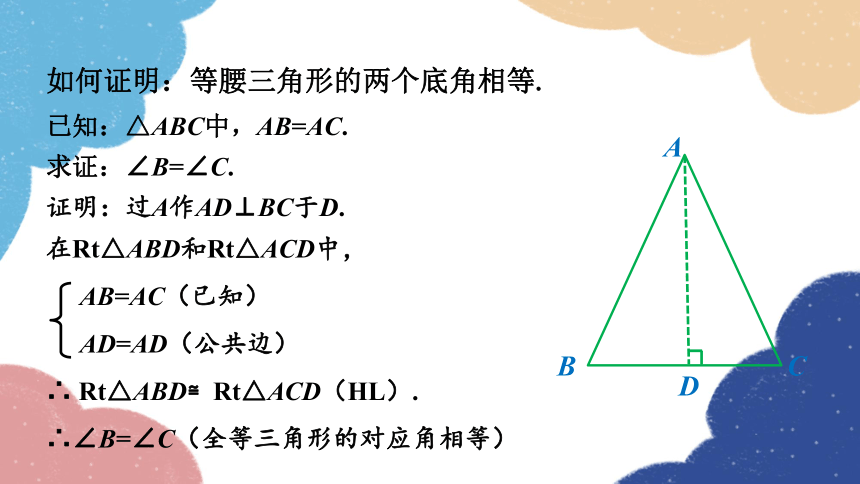
如何证明:等腰三角形的两个底角相等.
已知:△ABC中,AB=AC.
求证:∠B=∠C.
证明:过A作AD⊥BC于D.
在Rt△ABD和Rt△ACD中,
AB=AC(已知)
AD=AD(公共边)
∴ Rt△ABD≌Rt△ACD(HL).
∴∠B=∠C(全等三角形的对应角相等)
A
B
C
D
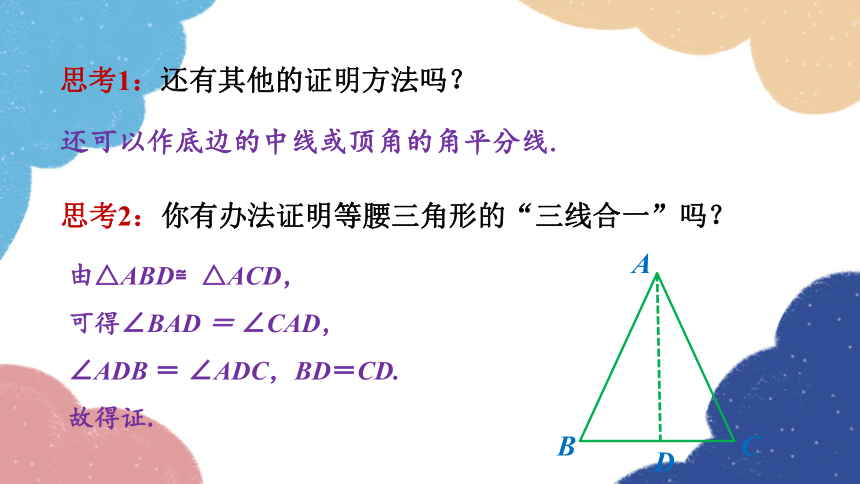
思考1:还有其他的证明方法吗?
思考2:你有办法证明等腰三角形的“三线合一”吗?
还可以作底边的中线或顶角的角平分线.
A
B
C
D
由△ABD≌△ACD,
可得∠BAD = ∠CAD,
∠ADB = ∠ADC,BD=CD.
故得证.
等腰三角形的性质
性质1:等腰三角形的两个底角相等(简称“等边对等角”)
A
B
C
D
几何语言:
在△ABC中,
∵AB=AC,
∴ ∠B=∠C.
性质2:等腰三角形的顶角平分线、底边上的高和底边上的中线互相重合(简称“三线合一”)
等腰三角形的性质
A
B
C
D
几何语言:
(1)∵AD⊥BC,∴∠BAD=∠CAD,BD=CD
(2)∵AD是中线,∴ AD⊥BC,∠ BAD=∠CAD
(3)∵AD是角平分线,∴ AD⊥BC,BD=CD
在△ABC中, AB=AC 时,
A
B
C
D
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,
∠A=∠ABD(等边对等角)
设∠A=x,
则∠BDC=∠A+∠ABD=2x,
从而∠ABC=∠C=∠BDC=2x,
x
2x
2x
2x
例1:如图,在△ABC中 ,AB=AC,点D在AC 上,且BD=BC=AD. 求△ABC各内角的度数?
于是在△ABC中,有
∠A+∠ABC+∠C=x+2x+2x=180°,
解得x=36°,
在△ABC中,∠A=36°
∠ABC=∠C=72°.
A
B
C
D
x
2x
2x
2x
例1:如图,在△ABC中 ,AB=AC,点D在AC 上,且BD=BC=AD. 求△ABC各内角的度数?
探究:∵AC=AB(已知)
∴∠B=∠C(等边对等角)
反过来,如果∠B=∠C,
那么AB=AC成立吗?
A
B
C
成立.
怎样进行验证?
A
B
C
D
证明:过A 点作AD⊥BC,垂足为D.
在△ABD 和△ACD 中,
∠B =∠C,
∠ADB = ∠ADC = 90°,
AD = AD,
∴ △ABD ≌△ACD(AAS) .
∴ AB = AC .
已知:在△ABC 中,∠B =∠C.
求证:AB =AC.
等腰三角形的判定方法
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).
在△ABC中,
∵∠B=∠C,
∴AC=AB.
几何语言:
A
B
C
例2:求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
求证:
A
B
C
D
E
1
2
已知:
AD平分∠CAE
AD∥BC
∠CAE是△ABC的外角
AB=AC
怎样证明命题?
方法:画图,结合图形,把命题写成
“已知…..,求证…….”的形式.
∵AD∥BC,
∴∠1=∠B(两直线平行, 同位角相等)
∴∠1=∠2(角平分线的定义 )
∴∠C=∠B(等量代换 )
∴ AB=AC(等角对等边 )
∠2=∠C(两直线平行,内错角相等)
证明:
∵ AD平分∠CAE,
A
B
C
D
E
1
2
1.如图,△ABC 中, AB =AC, ∠B=72°, 则∠C= .
2.如图,△ABC 中, AB =AC,
∠A =50°, 则∠B = .
A
B
C
A
B
C
65°
72°
随堂练习
3.已知: BD平分∠ABC , AD∥BC .
求证: AB=AD.
A
B
C
D
1
2
3
证明:
∵ BD平分∠ABC,
∴∠1=∠2(角平分线的定义)
∵AD∥BC,
∴∠1=∠3(两直线平行,内错角相等 )
∴∠2=∠3(等量代换 )
∴ AB=AD(等角对等边 )
13.3 等腰三角形
第1课时 等腰三角形
新课导入
A
B
C
△ABC有什么特点?
△ABD沿AD对折得到△ABC,
即AB=AC,
∴△ABC是等腰三角形.
D
A
B
C
D
将△ABC沿AD对折,你有什么发现?
(B)
重合的线段 重合的角
AB=AC
BD=CD
AD=AD
∠B = ∠C
∠BAD = ∠CAD
∠ADB = ∠ADC
等腰三角形除了两腰相等以外,你还能发现它的其他性质吗
1.∠B=∠C
2.BD=CD,AD为底边上的中线.
3.∠ADB=∠ADC=90°,AD为底边上的高.
4.∠BAD=∠CAD,AD为顶角平分线.
A
B
C
D
等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合(简写成“三线合一”)
问题2:结论2、3、4可以用一句话归纳吗?
问题1:结论1用文字如何表述?
等腰三角形的两个底角相等(简写“等边对等角”)
如何证明:等腰三角形的两个底角相等.
已知:△ABC中,AB=AC.
求证:∠B=∠C.
证明:过A作AD⊥BC于D.
在Rt△ABD和Rt△ACD中,
AB=AC(已知)
AD=AD(公共边)
∴ Rt△ABD≌Rt△ACD(HL).
∴∠B=∠C(全等三角形的对应角相等)
A
B
C
D
思考1:还有其他的证明方法吗?
思考2:你有办法证明等腰三角形的“三线合一”吗?
还可以作底边的中线或顶角的角平分线.
A
B
C
D
由△ABD≌△ACD,
可得∠BAD = ∠CAD,
∠ADB = ∠ADC,BD=CD.
故得证.
等腰三角形的性质
性质1:等腰三角形的两个底角相等(简称“等边对等角”)
A
B
C
D
几何语言:
在△ABC中,
∵AB=AC,
∴ ∠B=∠C.
性质2:等腰三角形的顶角平分线、底边上的高和底边上的中线互相重合(简称“三线合一”)
等腰三角形的性质
A
B
C
D
几何语言:
(1)∵AD⊥BC,∴∠BAD=∠CAD,BD=CD
(2)∵AD是中线,∴ AD⊥BC,∠ BAD=∠CAD
(3)∵AD是角平分线,∴ AD⊥BC,BD=CD
在△ABC中, AB=AC 时,
A
B
C
D
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,
∠A=∠ABD(等边对等角)
设∠A=x,
则∠BDC=∠A+∠ABD=2x,
从而∠ABC=∠C=∠BDC=2x,
x
2x
2x
2x
例1:如图,在△ABC中 ,AB=AC,点D在AC 上,且BD=BC=AD. 求△ABC各内角的度数?
于是在△ABC中,有
∠A+∠ABC+∠C=x+2x+2x=180°,
解得x=36°,
在△ABC中,∠A=36°
∠ABC=∠C=72°.
A
B
C
D
x
2x
2x
2x
例1:如图,在△ABC中 ,AB=AC,点D在AC 上,且BD=BC=AD. 求△ABC各内角的度数?
探究:∵AC=AB(已知)
∴∠B=∠C(等边对等角)
反过来,如果∠B=∠C,
那么AB=AC成立吗?
A
B
C
成立.
怎样进行验证?
A
B
C
D
证明:过A 点作AD⊥BC,垂足为D.
在△ABD 和△ACD 中,
∠B =∠C,
∠ADB = ∠ADC = 90°,
AD = AD,
∴ △ABD ≌△ACD(AAS) .
∴ AB = AC .
已知:在△ABC 中,∠B =∠C.
求证:AB =AC.
等腰三角形的判定方法
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).
在△ABC中,
∵∠B=∠C,
∴AC=AB.
几何语言:
A
B
C
例2:求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
求证:
A
B
C
D
E
1
2
已知:
AD平分∠CAE
AD∥BC
∠CAE是△ABC的外角
AB=AC
怎样证明命题?
方法:画图,结合图形,把命题写成
“已知…..,求证…….”的形式.
∵AD∥BC,
∴∠1=∠B(两直线平行, 同位角相等)
∴∠1=∠2(角平分线的定义 )
∴∠C=∠B(等量代换 )
∴ AB=AC(等角对等边 )
∠2=∠C(两直线平行,内错角相等)
证明:
∵ AD平分∠CAE,
A
B
C
D
E
1
2
1.如图,△ABC 中, AB =AC, ∠B=72°, 则∠C= .
2.如图,△ABC 中, AB =AC,
∠A =50°, 则∠B = .
A
B
C
A
B
C
65°
72°
随堂练习
3.已知: BD平分∠ABC , AD∥BC .
求证: AB=AD.
A
B
C
D
1
2
3
证明:
∵ BD平分∠ABC,
∴∠1=∠2(角平分线的定义)
∵AD∥BC,
∴∠1=∠3(两直线平行,内错角相等 )
∴∠2=∠3(等量代换 )
∴ AB=AD(等角对等边 )
