人教版数学八年级上册 11.3.1多边形课件(共20张PPT)
文档属性
| 名称 | 人教版数学八年级上册 11.3.1多边形课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 510.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-21 16:20:59 | ||
图片预览





文档简介
(共20张PPT)
11.3 多边形及其内角和
第1课时 多边形
学习目标
1.能从实物中辨别几何图形.
2.了解多边形及其相关概念.
3.掌握多边形的对角线的有关知识.
新课引入
从这些图中,你能抽象出什么平面图形?
新课引入
新课引入
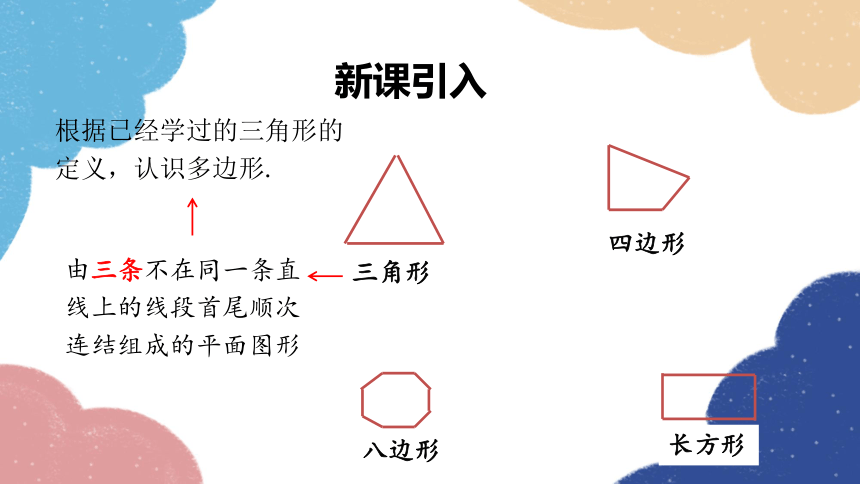
三角形
由三条不在同一条直线上的线段首尾顺次连结组成的平面图形
根据已经学过的三角形的定义,认识多边形.
四边形
长方形
八边形
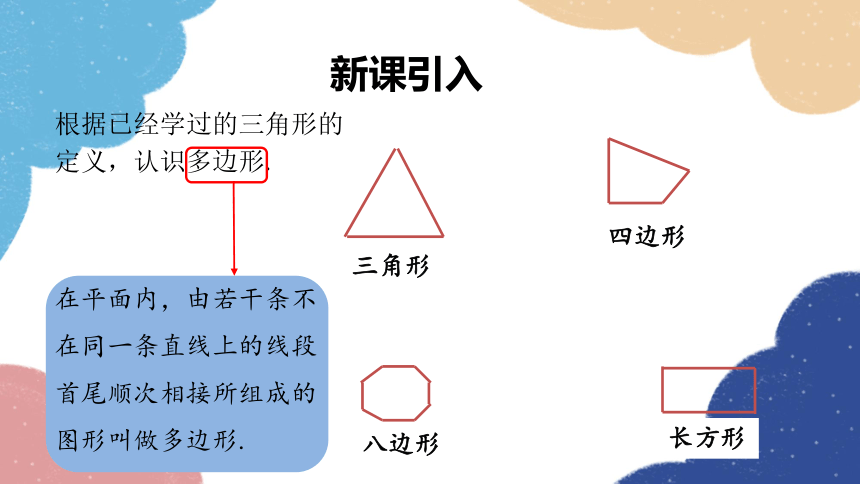
在平面内,由若干条不在同一条直线上的线段首尾顺次相接所组成的图形叫做多边形.
新课引入
三角形
根据已经学过的三角形的定义,认识多边形.
四边形
八边形
长方形
多边形按组成它的线段条数分成三角形、四边形、五边形……其中三角形是最简单的多边形.
如果一个多边形由n条线段组成,那么这个多边形就叫做n边形(n≥3).
知识讲解
n边形的定义
知识讲解
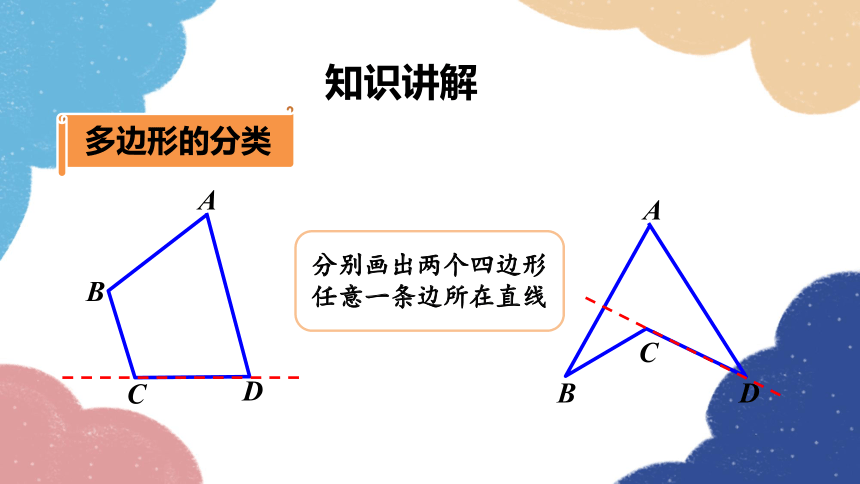
多边形的分类
A
B
C
D
A
B
D
C
分别画出两个四边形任意一条边所在直线
知识讲解
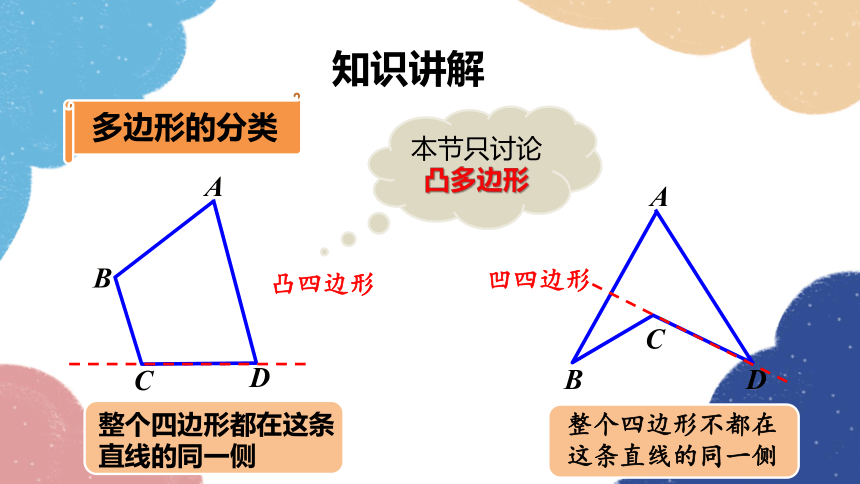
多边形的分类
A
B
C
D
B
D
整个四边形都在这条直线的同一侧
凸四边形
整个四边形不都在
这条直线的同一侧
凹四边形
本节只讨论凸多边形
A
C
知识讲解
多边形的相关概念
顶点
内角
边
五边形ABCDE
或五边形DCBAE
A
B
C
D
E
外角
多边形相邻两边组成的角
内角的邻补角
多边形的边与它的邻边的延长线组成的角
知识讲解
多边形的相关概念
顶点
内角
边
五边形ABCDE
或五边形DCBAE
A
B
C
D
E
外角
五边形:
5个顶点,
5条边,
5个内角,
10个外角.
知识讲解
多边形的相关概念
顶点
内角
边
五边形ABCDE
或五边形DCBAE
A
B
C
D
E
外角
n边形:
____个顶点,
____条边,
____个内角,
____个外角.
n
n
n
2n
对角线
A
B
C
D
E
知识讲解
多边形的相关概念
连接不相邻的两个顶点的线段
知识讲解
对角线的定义
连结多边形不相邻的两个顶点的线段,叫做多边形的对角线.
三角形
六边形
四边形
八边形
……..
五边形
画出下列图形从某一顶点出发的对角线:
从同一顶点引出的对角线的条数:
1
2
3
n-3
分割出的三角形的个数:
2
3
4
n-2
0
1
知识讲解
探究对角线的条数
n边形
……
三角形
四边形
五边形
六边形
……
……
边数 3 4 5 6 8 … n
从一个顶点出发的对角线的条数
上述对角线分成的三角形个数
总的对角线条数
0
1
0
1
2
2
2
3
5
3
4
9
5
6
20
n-3
n-2
n(n-3)
2
…
归纳小结
…
…
知识讲解
特殊的多边形
正方形的各个角都相等,各条边都相等.
像正方形这样,各个角都相等,各条边都相等的多边形叫做正多边形.
例如:
正三角形
正方形
正五边形
正六边形
随堂训练
1.多边形相邻两边组成的角叫做它的 ,如图所示的六边形的内角分别是 ;多边形的边与它的邻边的延长线组成的角叫做多边形的 ,如图所示, 是六边形的一个外角;连接多边形不相邻的两个顶点的线段,叫做多边形的 ,如图所示,线段 是六边形的一条对角线.
内角
∠FAB,∠B,∠BCD,∠CDE,∠E,∠F
外角
∠EDG
对角线
AC
2.从15边形的一个顶点可引出 条对角线,并把15边形分成 个三角形,15边形共有 条对角线.
随堂训练
12
13
90
3.下列语句正确的是( ).
A.四条边都相等的四边形是正多边形
B.四个角都相等的四边形是正多边形
C.等边三角形不是正多边形
D.正方形是正多边形
【解析】正多边形要求各边都相等,各角也都相等,两个条件缺一不可,矩形四个角都相等,但边不等.菱形四条边都相等,但角不等.等边三角形是正多边形.
故答案为D.
随堂训练
D
11.3 多边形及其内角和
第1课时 多边形
学习目标
1.能从实物中辨别几何图形.
2.了解多边形及其相关概念.
3.掌握多边形的对角线的有关知识.
新课引入
从这些图中,你能抽象出什么平面图形?
新课引入
新课引入
三角形
由三条不在同一条直线上的线段首尾顺次连结组成的平面图形
根据已经学过的三角形的定义,认识多边形.
四边形
长方形
八边形
在平面内,由若干条不在同一条直线上的线段首尾顺次相接所组成的图形叫做多边形.
新课引入
三角形
根据已经学过的三角形的定义,认识多边形.
四边形
八边形
长方形
多边形按组成它的线段条数分成三角形、四边形、五边形……其中三角形是最简单的多边形.
如果一个多边形由n条线段组成,那么这个多边形就叫做n边形(n≥3).
知识讲解
n边形的定义
知识讲解
多边形的分类
A
B
C
D
A
B
D
C
分别画出两个四边形任意一条边所在直线
知识讲解
多边形的分类
A
B
C
D
B
D
整个四边形都在这条直线的同一侧
凸四边形
整个四边形不都在
这条直线的同一侧
凹四边形
本节只讨论凸多边形
A
C
知识讲解
多边形的相关概念
顶点
内角
边
五边形ABCDE
或五边形DCBAE
A
B
C
D
E
外角
多边形相邻两边组成的角
内角的邻补角
多边形的边与它的邻边的延长线组成的角
知识讲解
多边形的相关概念
顶点
内角
边
五边形ABCDE
或五边形DCBAE
A
B
C
D
E
外角
五边形:
5个顶点,
5条边,
5个内角,
10个外角.
知识讲解
多边形的相关概念
顶点
内角
边
五边形ABCDE
或五边形DCBAE
A
B
C
D
E
外角
n边形:
____个顶点,
____条边,
____个内角,
____个外角.
n
n
n
2n
对角线
A
B
C
D
E
知识讲解
多边形的相关概念
连接不相邻的两个顶点的线段
知识讲解
对角线的定义
连结多边形不相邻的两个顶点的线段,叫做多边形的对角线.
三角形
六边形
四边形
八边形
……..
五边形
画出下列图形从某一顶点出发的对角线:
从同一顶点引出的对角线的条数:
1
2
3
n-3
分割出的三角形的个数:
2
3
4
n-2
0
1
知识讲解
探究对角线的条数
n边形
……
三角形
四边形
五边形
六边形
……
……
边数 3 4 5 6 8 … n
从一个顶点出发的对角线的条数
上述对角线分成的三角形个数
总的对角线条数
0
1
0
1
2
2
2
3
5
3
4
9
5
6
20
n-3
n-2
n(n-3)
2
…
归纳小结
…
…
知识讲解
特殊的多边形
正方形的各个角都相等,各条边都相等.
像正方形这样,各个角都相等,各条边都相等的多边形叫做正多边形.
例如:
正三角形
正方形
正五边形
正六边形
随堂训练
1.多边形相邻两边组成的角叫做它的 ,如图所示的六边形的内角分别是 ;多边形的边与它的邻边的延长线组成的角叫做多边形的 ,如图所示, 是六边形的一个外角;连接多边形不相邻的两个顶点的线段,叫做多边形的 ,如图所示,线段 是六边形的一条对角线.
内角
∠FAB,∠B,∠BCD,∠CDE,∠E,∠F
外角
∠EDG
对角线
AC
2.从15边形的一个顶点可引出 条对角线,并把15边形分成 个三角形,15边形共有 条对角线.
随堂训练
12
13
90
3.下列语句正确的是( ).
A.四条边都相等的四边形是正多边形
B.四个角都相等的四边形是正多边形
C.等边三角形不是正多边形
D.正方形是正多边形
【解析】正多边形要求各边都相等,各角也都相等,两个条件缺一不可,矩形四个角都相等,但边不等.菱形四条边都相等,但角不等.等边三角形是正多边形.
故答案为D.
随堂训练
D
