黑龙江省哈尔滨市巴彦县重点中学2022--2023学年八年级下学期期中数学试题(含答案)
文档属性
| 名称 | 黑龙江省哈尔滨市巴彦县重点中学2022--2023学年八年级下学期期中数学试题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-21 12:14:34 | ||
图片预览


文档简介
2022-2023学年度下学期八年级期中考试题
数学试卷
考生须知:
1.本试卷满分为120分。考试时间为120分钟。
2.答题前,考生先将自己的“姓名”、“考号”、“考场”、“座位号”在答题卡上填写清楚,将“条形码”准确补贴在条形码区域内。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题纸上答题无效。
4.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
5.保持卡面整洁,不要折叠、不要弄脏、弄皱,不准使用涂改波、刮纸刀。
第Ⅰ卷 选择题(共30分)(涂卡)
一、选择题(每小题3分,共计30分)
1.实数的倒数是( )
A. B. C. D.
2.下列计算不正确的是( )
A. B. C. D.
3.下列图形中,不是轴对称图形的是( )
A.矩形 B.菱形 C.等腰三角形 D.平行四边形
4.下列各组数中,不能构成直角三角形三边长的是( )
A.10,8,6 B.1,1, C.5,12,13 D.1,2,3
5.下列说法正确的是( )
A.平行线间的距离处处相等 B.菱形的对角线相等
C.对角线互相垂直的四边形是平行四边形 D.直角三角形斜边中线等于直角边的一半
6.如图,在四边形中,,添加下列一个条件后,一定能判定四边形是平行四边形的是( )
A. B. C. D.
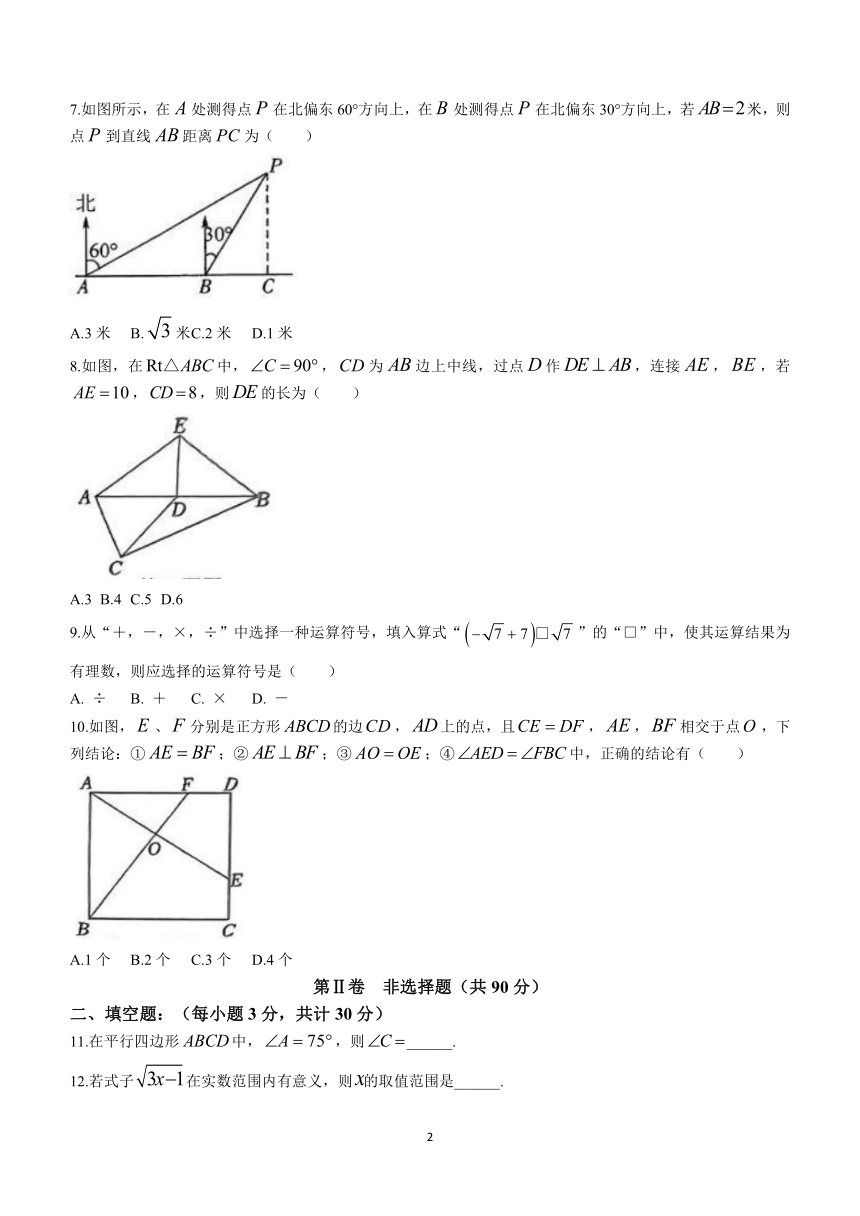
7.如图所示,在处测得点在北偏东60°方向上,在处测得点在北偏东30°方向上,若米,则点到直线距离为( )
A.3米 B.米 C.2米 D.1米
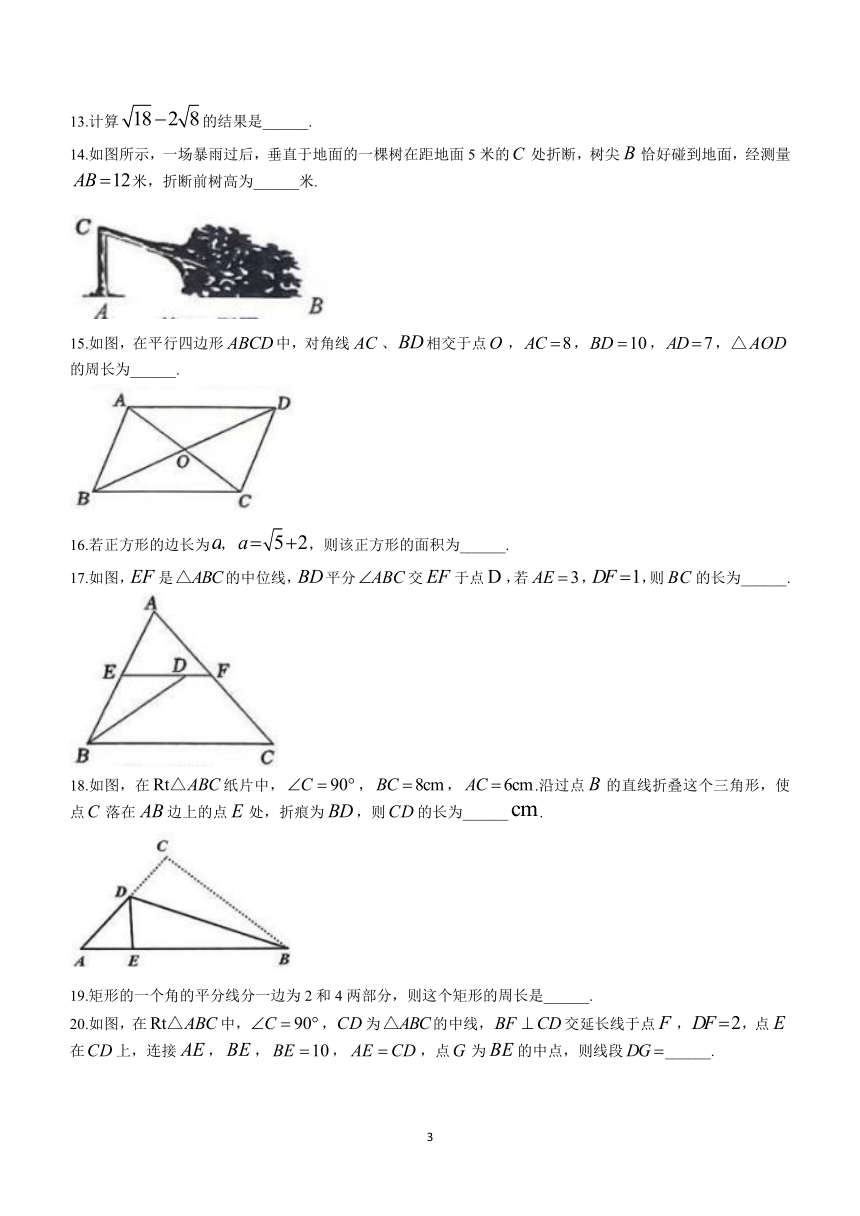
8.如图,在中,,为边上中线,过点作,连接,,若,,则的长为( )
A.3 B.4 C.5 D.6
9.从“+,-,×,÷”中选择一种运算符号,填入算式“”的“□”中,使其运算结果为有理数,则应选择的运算符号是( )
A. ÷ B. + C. × D. -
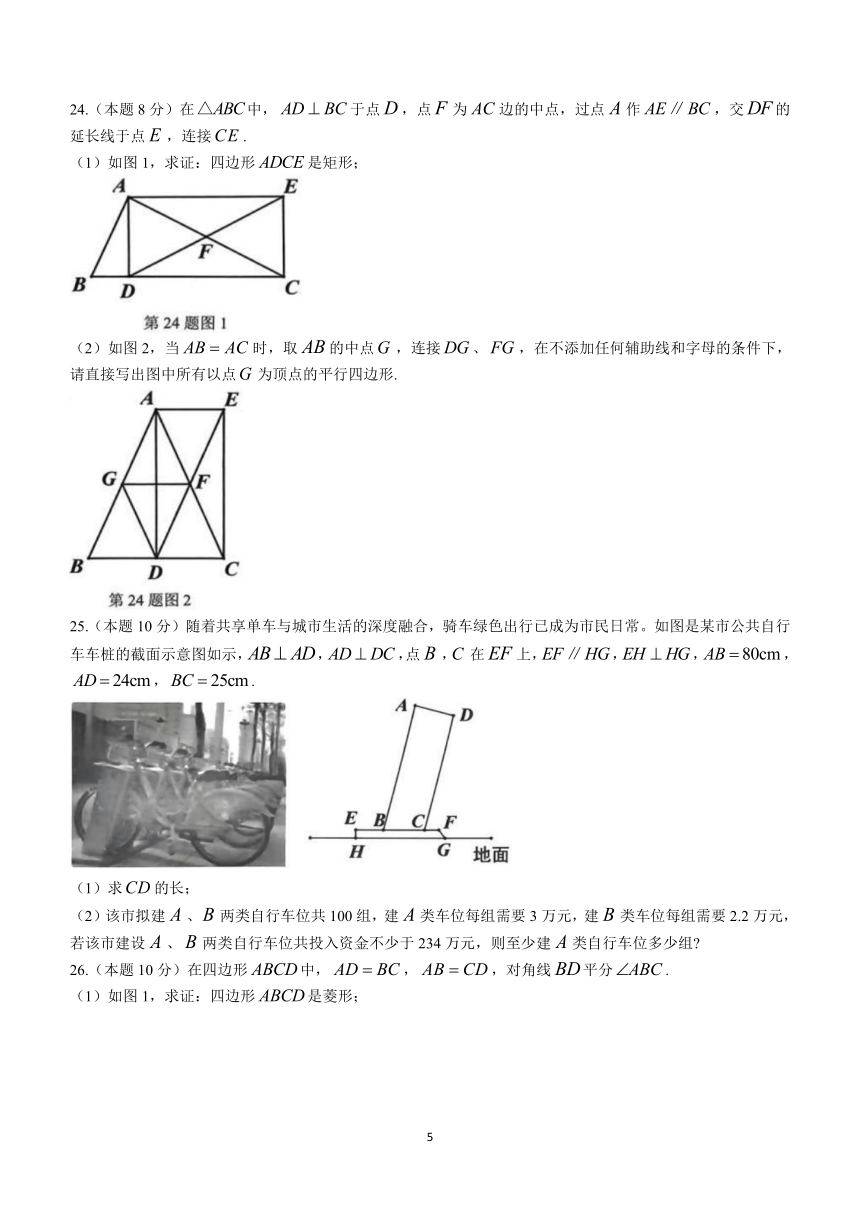
10.如图,、分别是正方形的边,上的点,且,,相交于点,下列结论:①;②;③;④中,正确的结论有( )
A.1个 B.2个 C.3个 D.4个
第Ⅱ卷 非选择题(共90分)
二、填空题:(每小题3分,共计30分)
11.在平行四边形中,,则______.
12.若式子在实数范围内有意义,则的取值范围是______.
13.计算的结果是______.
14.如图所示,一场暴雨过后,垂直于地面的一棵树在距地面5米的处折断,树尖恰好碰到地面,经测量米,折断前树高为______米.
15.如图,在平行四边形中,对角线、相交于点,,,,的周长为______.
16.若正方形的边长为,,则该正方形的面积为______.
17.如图,是的中位线,平分交于点,若,,则的长为______.
18.如图,在纸片中,,,.沿过点的直线折叠这个三角形,使点落在边上的点处,折痕为,则的长为______.
19.矩形的一个角的平分线分一边为2和4两部分,则这个矩形的周长是______.
20.如图,在中,,为的中线,交延长线于点,,点在上,连接,,,,点为的中点,则线段______.
三、解答题(21、22题各7分,23、24题各8分,25、26、27题各10分,共60分)
21.(本题7分)先化简,再求值:,其中
22.(本原7分)图1,图2,是二张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1.请在图1,图2中,分别画一个符合要求的图形.
要求:所画的图形各顶点必须与方格纸中的小正方形顶点重合.
(1)画一个周长为22,面积为30的矩形;
(2)画一个周长为的菱形(非正方形).
23.(本题8分)如图,李叔叔家有一块矩形空地,矩形空地的长为米,宽为米,现要在空地中划出一块矩形地养鸡(即图中阴影部分),其余部分种植蔬菜,矩形养鸡场的长为米,宽为米.
(1)矩形的周长是多少米?
(2)若市场上蔬菜的价格是8元/千克,李叔叔种植该种蔬菜,每平方米可以产15千克的蔬菜,李叔叔如果将所种蔬菜全部销售完,销售收入为多少元?
24.(本题8分)在中,于点,点为边的中点,过点作,交的延长线于点,连接.
(1)如图1,求证:四边形是矩形;
(2)如图2,当时,取的中点,连接、,在不添加任何辅助线和字母的条件下,请直接写出图中所有以点为顶点的平行四边形.
25.(本题10分)随着共享单车与城市生活的深度融合,骑车绿色出行已成为市民日常。如图是某市公共自行车车桩的截面示意图如示,,,点,在上,,,,,.
(1)求的长;
(2)该市拟建、两类自行车位共100组,建类车位每组需要3万元,建类车位每组需要2.2万元,若该市建设、两类自行车位共投入资金不少于234万元,则至少建类自行车位多少组
26.(本题10分)在四边形中,,,对角线平分.
(1)如图1,求证:四边形是菱形;
(2)如图2,点在上,点在射线上,连接,,的角平分线交于点,若,求证:;
(3)如图3,在(2)的条件下,若,连接,,,求线段的长.
27.(本题10分)如图1,在平面直角坐标系中,点为坐标原点,点在轴上,点在第一象限内,连接,,过点作轴于点,连接,若.
(1)求点的坐标;
(2)点从点以每秒1个单位的长度沿射线方向运动,设点运动的时间为、、、、四点组成的面积为,请用含的式子表示;
(3)在(2)的条件下,点为中点,连接并延长交轴于点,点为平面内一点,若点、、、四点组成的四边形为菱形,求点的坐标.
2022-2023学年度下学期八年级期中考试题
数学试卷参考答案
一、选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 A C D D A C B D B C
二、填空题:
题号 1 2 3 4 5 6 7 8 9 10
答案 75 18 16 8 18或20
三、解答题:
21.(1)解:原式.................1'
.................1'
.................1'
.................1'
∵
∴原式.................3'
22.(1)画图正确...........3'
(2)画图正确...........4'
23.(1).................1'
................2'
.................1'
(2).................2'
.................1'
(元).................1'
答:销售收入为4680元。
24.(1)∵为的中点
∴
∵
∴,
∴
∴
∴四边形是平行四边形
∵
∴
∴四边形是矩形
(2)平行四边形、平行四边形、平行四边形、平行四边形.......4'(每个一分)
25.(1)过点作于点
∴
∵,
∴
∴四边形是矩形.................2'
∴,.................1'
在中,
∴.................1'
∴
∴.................1'
(2)设建类自行车位组.................1'
.................2'
解得.................1'
答:至少建类自行车位40组。.................1'
26.(1)证明:∵,
∴四边形是平行四边形,.................1'
∵平分
∴
∴.................1'
∴
∴四边形是菱形.................1'
(2)∵平分
∴
∵
∴
∵
∴
∴.................1'
∵四边形是菱形
∴.................1'
∴
∴.................1'
(3)∵,
∴
过点作交的延长线于点,作于点
∴
∵
∴
∴,.................1'
∵
∴
∴,.................1'
∵
∴
∵
∴.................1'
∴
∴
∴.................1'
27.(1)∵
∴
∵
∴
∴.................1'
∵轴
∴
∵
∴四边形是矩形
∵
∴
∴.................1'
(2)由题意得,,
①当点在上时,
∴.................2'
②当点在延长线上时,
∴.................2'
(3)∵为中点
∴
∵,
∴
∴.................1'
①当点在线段上时,
设,∴
在中,
即
解得
∴
∵
∴当时,四边形是菱形
∴
∵
∴
过点作轴于点
∴四边形为矩形
∴
∴.................1'
②当点在的延长线上时,
在中
∴.................1'
∵
∴时,四边形是菱形
∴
∵
∴
∴.................1'
综上所述,点或
数学试卷
考生须知:
1.本试卷满分为120分。考试时间为120分钟。
2.答题前,考生先将自己的“姓名”、“考号”、“考场”、“座位号”在答题卡上填写清楚,将“条形码”准确补贴在条形码区域内。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题纸上答题无效。
4.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
5.保持卡面整洁,不要折叠、不要弄脏、弄皱,不准使用涂改波、刮纸刀。
第Ⅰ卷 选择题(共30分)(涂卡)
一、选择题(每小题3分,共计30分)
1.实数的倒数是( )
A. B. C. D.
2.下列计算不正确的是( )
A. B. C. D.
3.下列图形中,不是轴对称图形的是( )
A.矩形 B.菱形 C.等腰三角形 D.平行四边形
4.下列各组数中,不能构成直角三角形三边长的是( )
A.10,8,6 B.1,1, C.5,12,13 D.1,2,3
5.下列说法正确的是( )
A.平行线间的距离处处相等 B.菱形的对角线相等
C.对角线互相垂直的四边形是平行四边形 D.直角三角形斜边中线等于直角边的一半
6.如图,在四边形中,,添加下列一个条件后,一定能判定四边形是平行四边形的是( )
A. B. C. D.
7.如图所示,在处测得点在北偏东60°方向上,在处测得点在北偏东30°方向上,若米,则点到直线距离为( )
A.3米 B.米 C.2米 D.1米
8.如图,在中,,为边上中线,过点作,连接,,若,,则的长为( )
A.3 B.4 C.5 D.6
9.从“+,-,×,÷”中选择一种运算符号,填入算式“”的“□”中,使其运算结果为有理数,则应选择的运算符号是( )
A. ÷ B. + C. × D. -
10.如图,、分别是正方形的边,上的点,且,,相交于点,下列结论:①;②;③;④中,正确的结论有( )
A.1个 B.2个 C.3个 D.4个
第Ⅱ卷 非选择题(共90分)
二、填空题:(每小题3分,共计30分)
11.在平行四边形中,,则______.
12.若式子在实数范围内有意义,则的取值范围是______.
13.计算的结果是______.
14.如图所示,一场暴雨过后,垂直于地面的一棵树在距地面5米的处折断,树尖恰好碰到地面,经测量米,折断前树高为______米.
15.如图,在平行四边形中,对角线、相交于点,,,,的周长为______.
16.若正方形的边长为,,则该正方形的面积为______.
17.如图,是的中位线,平分交于点,若,,则的长为______.
18.如图,在纸片中,,,.沿过点的直线折叠这个三角形,使点落在边上的点处,折痕为,则的长为______.
19.矩形的一个角的平分线分一边为2和4两部分,则这个矩形的周长是______.
20.如图,在中,,为的中线,交延长线于点,,点在上,连接,,,,点为的中点,则线段______.
三、解答题(21、22题各7分,23、24题各8分,25、26、27题各10分,共60分)
21.(本题7分)先化简,再求值:,其中
22.(本原7分)图1,图2,是二张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1.请在图1,图2中,分别画一个符合要求的图形.
要求:所画的图形各顶点必须与方格纸中的小正方形顶点重合.
(1)画一个周长为22,面积为30的矩形;
(2)画一个周长为的菱形(非正方形).
23.(本题8分)如图,李叔叔家有一块矩形空地,矩形空地的长为米,宽为米,现要在空地中划出一块矩形地养鸡(即图中阴影部分),其余部分种植蔬菜,矩形养鸡场的长为米,宽为米.
(1)矩形的周长是多少米?
(2)若市场上蔬菜的价格是8元/千克,李叔叔种植该种蔬菜,每平方米可以产15千克的蔬菜,李叔叔如果将所种蔬菜全部销售完,销售收入为多少元?
24.(本题8分)在中,于点,点为边的中点,过点作,交的延长线于点,连接.
(1)如图1,求证:四边形是矩形;
(2)如图2,当时,取的中点,连接、,在不添加任何辅助线和字母的条件下,请直接写出图中所有以点为顶点的平行四边形.
25.(本题10分)随着共享单车与城市生活的深度融合,骑车绿色出行已成为市民日常。如图是某市公共自行车车桩的截面示意图如示,,,点,在上,,,,,.
(1)求的长;
(2)该市拟建、两类自行车位共100组,建类车位每组需要3万元,建类车位每组需要2.2万元,若该市建设、两类自行车位共投入资金不少于234万元,则至少建类自行车位多少组
26.(本题10分)在四边形中,,,对角线平分.
(1)如图1,求证:四边形是菱形;
(2)如图2,点在上,点在射线上,连接,,的角平分线交于点,若,求证:;
(3)如图3,在(2)的条件下,若,连接,,,求线段的长.
27.(本题10分)如图1,在平面直角坐标系中,点为坐标原点,点在轴上,点在第一象限内,连接,,过点作轴于点,连接,若.
(1)求点的坐标;
(2)点从点以每秒1个单位的长度沿射线方向运动,设点运动的时间为、、、、四点组成的面积为,请用含的式子表示;
(3)在(2)的条件下,点为中点,连接并延长交轴于点,点为平面内一点,若点、、、四点组成的四边形为菱形,求点的坐标.
2022-2023学年度下学期八年级期中考试题
数学试卷参考答案
一、选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 A C D D A C B D B C
二、填空题:
题号 1 2 3 4 5 6 7 8 9 10
答案 75 18 16 8 18或20
三、解答题:
21.(1)解:原式.................1'
.................1'
.................1'
.................1'
∵
∴原式.................3'
22.(1)画图正确...........3'
(2)画图正确...........4'
23.(1).................1'
................2'
.................1'
(2).................2'
.................1'
(元).................1'
答:销售收入为4680元。
24.(1)∵为的中点
∴
∵
∴,
∴
∴
∴四边形是平行四边形
∵
∴
∴四边形是矩形
(2)平行四边形、平行四边形、平行四边形、平行四边形.......4'(每个一分)
25.(1)过点作于点
∴
∵,
∴
∴四边形是矩形.................2'
∴,.................1'
在中,
∴.................1'
∴
∴.................1'
(2)设建类自行车位组.................1'
.................2'
解得.................1'
答:至少建类自行车位40组。.................1'
26.(1)证明:∵,
∴四边形是平行四边形,.................1'
∵平分
∴
∴.................1'
∴
∴四边形是菱形.................1'
(2)∵平分
∴
∵
∴
∵
∴
∴.................1'
∵四边形是菱形
∴.................1'
∴
∴.................1'
(3)∵,
∴
过点作交的延长线于点,作于点
∴
∵
∴
∴,.................1'
∵
∴
∴,.................1'
∵
∴
∵
∴.................1'
∴
∴
∴.................1'
27.(1)∵
∴
∵
∴
∴.................1'
∵轴
∴
∵
∴四边形是矩形
∵
∴
∴.................1'
(2)由题意得,,
①当点在上时,
∴.................2'
②当点在延长线上时,
∴.................2'
(3)∵为中点
∴
∵,
∴
∴.................1'
①当点在线段上时,
设,∴
在中,
即
解得
∴
∵
∴当时,四边形是菱形
∴
∵
∴
过点作轴于点
∴四边形为矩形
∴
∴.................1'
②当点在的延长线上时,
在中
∴.................1'
∵
∴时,四边形是菱形
∴
∵
∴
∴.................1'
综上所述,点或
同课章节目录
