立体图形的表面积和体积计算总复习(课件)-六年级下册数学苏教版(共25张PPT)
文档属性
| 名称 | 立体图形的表面积和体积计算总复习(课件)-六年级下册数学苏教版(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-21 07:01:41 | ||
图片预览





文档简介
(共25张PPT)
立体图形的表面积和体积计算
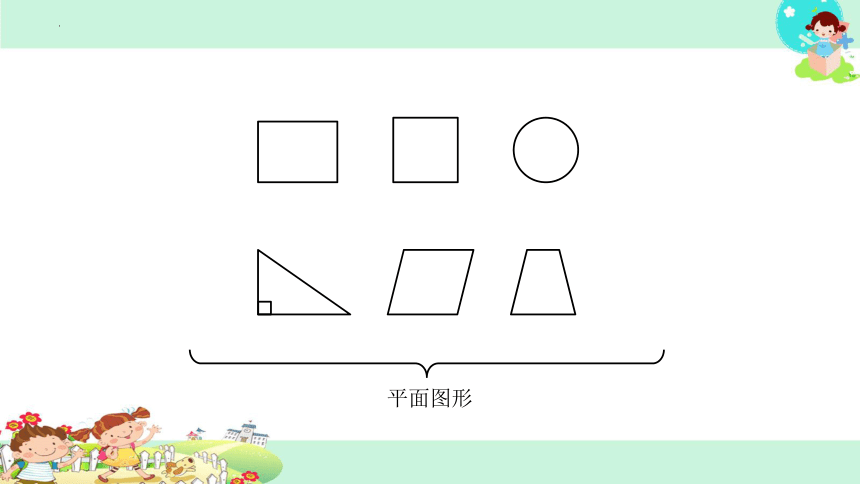
总复面图形
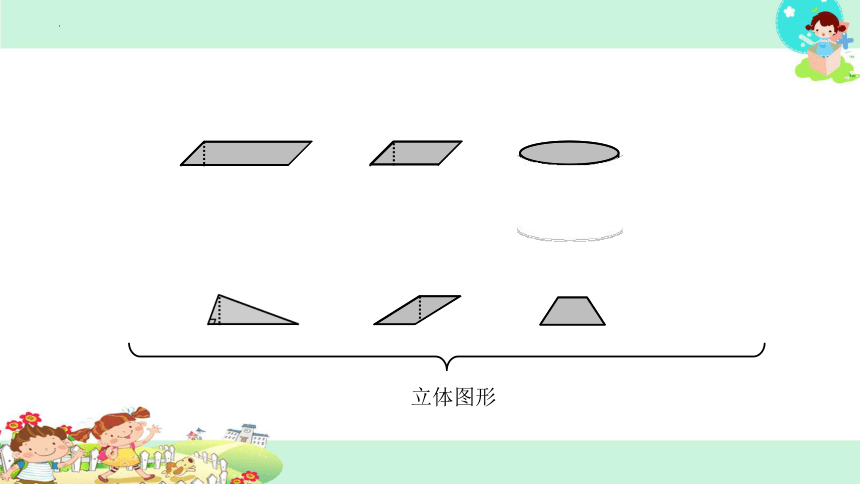
立体图形
观察并讨论:这些立体图形有什么共同点?
完成自主学习第1题
上下两个面互相平行
(高有无数条)
侧面和底面互相垂直
上下两个面互相平行
(高有无数条)
从上到下大小、形状完全相同
上下两个面互相平行
(高有无数条)
直柱体
侧面和底面互相垂直
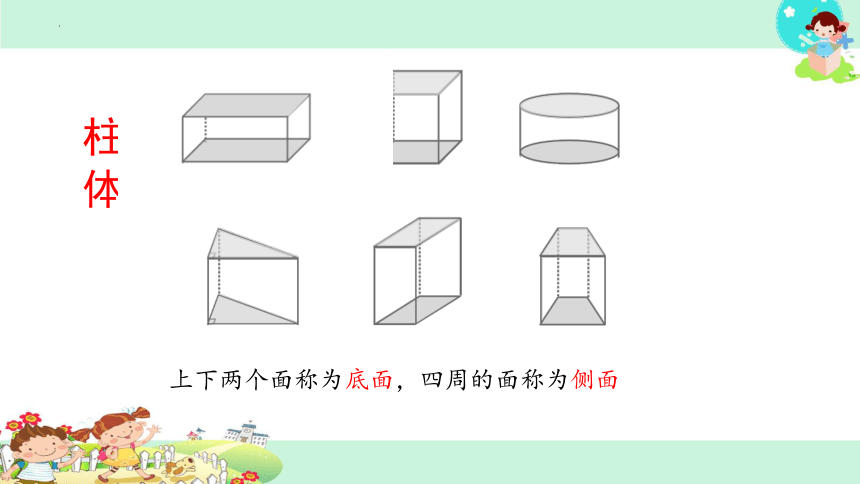
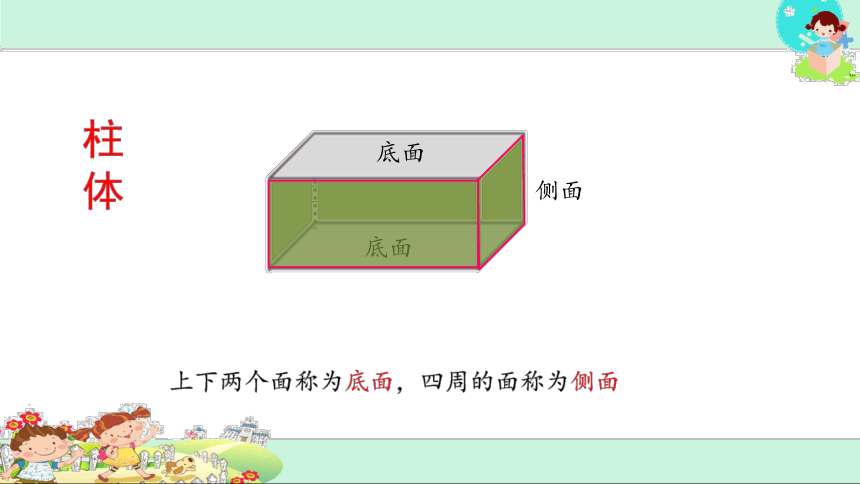
柱体
上下两个面称为底面,四周的面称为侧面
底面
底面
侧面
沿高将侧面展开,会得到怎样的图形呢?
想一想,画一画,填一填,完成自主学习第2题。
柱体
2.画出侧面展开示意图,再填空。
(1)将这些柱体的侧面沿高展开得到一个( )形,它的一条边是柱体的( ),另一条边是柱体的( )。计算柱体的侧面积,就是计算展开的( )的面积。可以用( )乘( )。
长方
高
底面周长
长方形
底面周长
高
(2)计算柱体的侧面积。
侧面积 = 底面周长×高
(3+2)×2×1= 10 cm2
2×4×2= 16 cm2
1×2×π×1 = 2π cm2
侧面积 = 底面周长×高
猜想
柱体的
验证
验证猜想
1.将长方形纸沿虚线对折,围成立体图形,连接处不重叠。
2.思考: (1)长方形的长和宽与围成的立体图形有什么关系?(2)长方形的面积和围成的立体图形的侧面积是什么关系?(3)围成的立体图形的侧面积可以怎样计算?
分享:将长方形纸沿虚线对折,围成一个柱体,长方形的一条边是柱体的( ),另一条边是柱体的( ); 长方形纸的面积就是柱体的( ),可以用柱体的( )乘( )计算柱体的侧面积。
猜想
验证
结论
应用
试一试:计算下面图形的表面积。
4cm
3cm
5cm
3cm
上下面积:
3×4 = 12 cm2
侧面积:
(3+4+5)×3 = 36 cm2
表面积:
12 + 36 = 48 cm2
应用
想一想,柱体的体积可以怎样计算呢?
a
b
h
a
a
a
·o
r
h
探究
V=
V=
V=
V=
猜想:柱体的体积=底面积×高
abh
a3
h
h
验证猜想:柱体的体积=底面积×高
4×3×3
4×3÷2×3 = 18 cm3
底面积
高
× = 体积
结论: 体积 = 底面积×高
÷2
= 18 cm3
验证猜想:柱体的体积=底面积×高
结论: 体积 = 底面积×高
验证猜想:柱体的体积=底面积×高
结论: 体积 = 底面积×高
结论:
柱体的体积=底面积×高
应用
计算这条拦河坝的体积。
(13+3)×5÷2×80 = 3200 m3
应用
一根圆柱形木棒,直径10厘米,高20厘米。沿着直径锯成相等的两块,每块的表面积和体积分别是多少?
上下面积:
(10÷2)2×3.14 = 78.5 cm2
侧面积:
(10+10×3.14÷2)×20 = 514 cm2
表面积:
78.5+514 = 592.5 cm2
体积:
78.5×20÷2 = 785 cm2
10cm
20cm
答:每块的表面积是592.5平方厘米,体积分别是785平方厘米。
学习回顾
收获:
直柱体的特点
直柱体侧面积的计算方法
直柱体体积的计算方法
探究学习的一般方法
两个底面互相平行
侧面和底面互相垂直
从上到下大小、形状完全相同
柱体侧面积=底面周长×高
柱体体积=底面积×高
提出猜想
验证猜想
得出结论
应用反思
立体图形的表面积和体积计算
总复面图形
立体图形
观察并讨论:这些立体图形有什么共同点?
完成自主学习第1题
上下两个面互相平行
(高有无数条)
侧面和底面互相垂直
上下两个面互相平行
(高有无数条)
从上到下大小、形状完全相同
上下两个面互相平行
(高有无数条)
直柱体
侧面和底面互相垂直
柱体
上下两个面称为底面,四周的面称为侧面
底面
底面
侧面
沿高将侧面展开,会得到怎样的图形呢?
想一想,画一画,填一填,完成自主学习第2题。
柱体
2.画出侧面展开示意图,再填空。
(1)将这些柱体的侧面沿高展开得到一个( )形,它的一条边是柱体的( ),另一条边是柱体的( )。计算柱体的侧面积,就是计算展开的( )的面积。可以用( )乘( )。
长方
高
底面周长
长方形
底面周长
高
(2)计算柱体的侧面积。
侧面积 = 底面周长×高
(3+2)×2×1= 10 cm2
2×4×2= 16 cm2
1×2×π×1 = 2π cm2
侧面积 = 底面周长×高
猜想
柱体的
验证
验证猜想
1.将长方形纸沿虚线对折,围成立体图形,连接处不重叠。
2.思考: (1)长方形的长和宽与围成的立体图形有什么关系?(2)长方形的面积和围成的立体图形的侧面积是什么关系?(3)围成的立体图形的侧面积可以怎样计算?
分享:将长方形纸沿虚线对折,围成一个柱体,长方形的一条边是柱体的( ),另一条边是柱体的( ); 长方形纸的面积就是柱体的( ),可以用柱体的( )乘( )计算柱体的侧面积。
猜想
验证
结论
应用
试一试:计算下面图形的表面积。
4cm
3cm
5cm
3cm
上下面积:
3×4 = 12 cm2
侧面积:
(3+4+5)×3 = 36 cm2
表面积:
12 + 36 = 48 cm2
应用
想一想,柱体的体积可以怎样计算呢?
a
b
h
a
a
a
·o
r
h
探究
V=
V=
V=
V=
猜想:柱体的体积=底面积×高
abh
a3
h
h
验证猜想:柱体的体积=底面积×高
4×3×3
4×3÷2×3 = 18 cm3
底面积
高
× = 体积
结论: 体积 = 底面积×高
÷2
= 18 cm3
验证猜想:柱体的体积=底面积×高
结论: 体积 = 底面积×高
验证猜想:柱体的体积=底面积×高
结论: 体积 = 底面积×高
结论:
柱体的体积=底面积×高
应用
计算这条拦河坝的体积。
(13+3)×5÷2×80 = 3200 m3
应用
一根圆柱形木棒,直径10厘米,高20厘米。沿着直径锯成相等的两块,每块的表面积和体积分别是多少?
上下面积:
(10÷2)2×3.14 = 78.5 cm2
侧面积:
(10+10×3.14÷2)×20 = 514 cm2
表面积:
78.5+514 = 592.5 cm2
体积:
78.5×20÷2 = 785 cm2
10cm
20cm
答:每块的表面积是592.5平方厘米,体积分别是785平方厘米。
学习回顾
收获:
直柱体的特点
直柱体侧面积的计算方法
直柱体体积的计算方法
探究学习的一般方法
两个底面互相平行
侧面和底面互相垂直
从上到下大小、形状完全相同
柱体侧面积=底面周长×高
柱体体积=底面积×高
提出猜想
验证猜想
得出结论
应用反思
