5.1.1任意角课件-2023-2024学年高一上学期数学人教A版(2019)必修第一册(共18张PPT)
文档属性
| 名称 | 5.1.1任意角课件-2023-2024学年高一上学期数学人教A版(2019)必修第一册(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-21 09:43:36 | ||
图片预览





文档简介
(共18张PPT)
5.1.1 任意角
体操是力与美的结合,也充满了角的概念.在匈牙利德布勒森举行的第36届世界体操锦标赛中,“李小鹏跳”——“踺子后手翻转体180度接直体前空翻转体900度”,震惊四座,这里的转体180度、 转体900度就是一个角的概念.
初中角的定义:
从一个点出发引出的两条射线构成的
几何图形(0°,360°)
“旋转”形成角
角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形.
1、角的范围
o
A
B
始边
终边
顶点
1、花样游泳中,运动员旋转的周数如何
用角度计算来表示?
2、汽车在前进和倒车中,车轮转动的角度
如何表示才比较合理?
3、工人在拧紧或拧松螺丝时,转动的角度
如何表示才比较合适?
正角:按逆时针方向旋转形成的角
负角:按顺时针方向旋转形成的角
零角:一条射线没有作任何旋转形 成的角
任意角
x
y
o
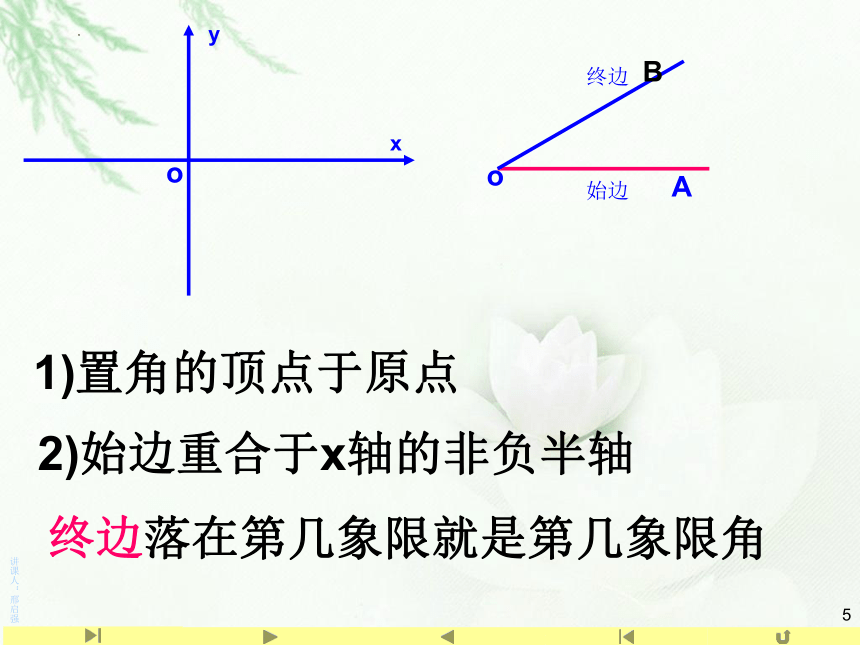
1)置角的顶点于原点
终边落在第几象限就是第几象限角
2)始边重合于x轴的非负半轴
始边
终边
A
B
o
练习
1、判断
1)、第一象限角都是锐角( )
2)、锐角都是第一象限角( )
3)、小于90°的角都是锐角( )
2、A={小于90°的角},B={第一象限角},则A∩B=( )
A、{锐角} B、{小于90°的角}
C、{第一象限角} D、以上都不对
√
×
×
D
x
y
o
300
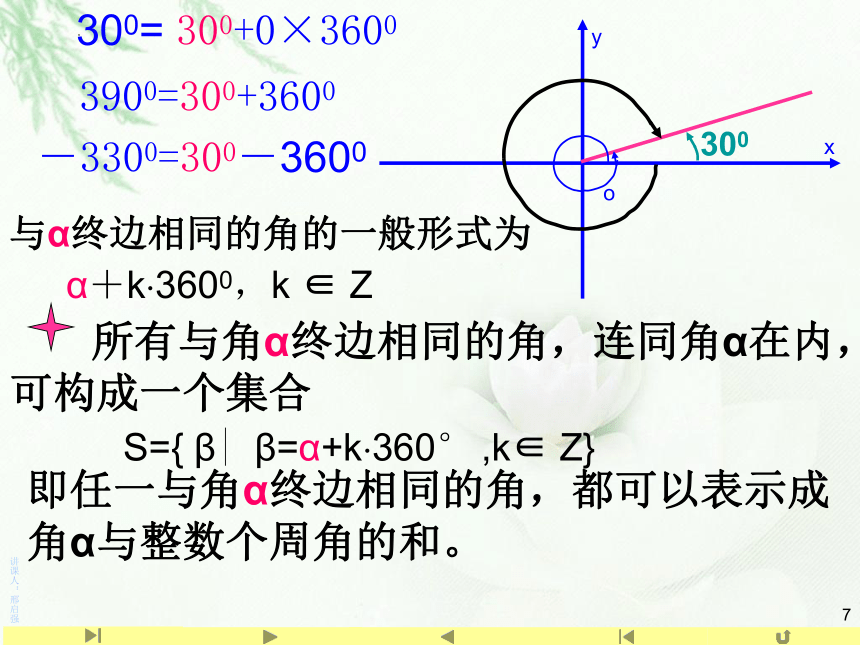
3900=300+3600
-3300=300-3600
300= 300+0×3600
与α终边相同的角的一般形式为
α+k 3600,k ∈ Z
S={ β| β=α+k 360° ,k∈ Z}
所有与角α终边相同的角,连同角α在内,可构成一个集合
即任一与角α终边相同的角,都可以表示成角α与整数个周角的和。
反思:
终边相同的角 相等;
但相等的角,终边 相同;
终边相同的角有无数多个,
它们相差 360°的整数倍.
不一定
一定
例1 把下列各角写成α+k 3600 (00≤a<3600,k∈z)的形式,并判定它们分别是第几象限角。
–120°; (2)660°;(3)-950°08′.
∴与 角终边相同的角是 角,
(1)∵
它是第三象限的角;
解:
∴与 角终边相同的角是 角,
它是第四象限的角;
(2)∵
所以与 角终边相同的角是 ,
(3)
它是第二象限角.
变式:写出与下列终边相同的角的集合,并写出-720°~360°间角.
(1)120°;
(2)-270°;
(3)1020°
-600°, -240°,120°
(2) -630°, -270°,90°
(3) -420°, -60°,300°
终边落在坐标轴上的情形
x
y
o
00
900
1800
2700
+ k 360°
+ k 360°
+ k 360°
+ k 360°
或3600+ k 360°
例2 写出终边落在y轴上的角的集合。
解:终边落在y轴非负半轴上的角的集合为
S1={β| β=900+k 3600,k∈Z}
={β| β=900+2k·1800 ,k∈Z}
终边落在y轴非正半轴上的角的集合为
S2={β| β=2700+k 3600,k∈Z}
={β| β=900+(2k+1) ·1800 ,k∈Z}
S=S1∪S2
所以终边落在y轴上的角的集合为
={β| β=900+n 1800 ,n∈Z}
x
y
O
900+k 3600
2700+k 3600
用集合表示各象限角的集合。
第一象限角
第二象限角
第三象限角
第四象限角
例3、写出终边在直线y=x上的角的集合S,并把S中适合不等式-360°≤β<720°的元素 写出来。
x
y
O
-315°, 45°,405°
动手试试
练 1. 如图,终边落在 OA位置时的角的集合是 :
终边落在OB 位置,且在-360°~360°内的角的集合是 ;
终边落在阴影部分(含边界)的角的集合是 .
小结:
角的分类
象限角及表示
终边相同角
角的定义与表示
正角,负角,零角
终边相同角应用
判断角在第几象限
特殊终边角
在给定范围内求角
以后解决问题时要意识到任意角为前提条件
提醒:
5.1.1 任意角
体操是力与美的结合,也充满了角的概念.在匈牙利德布勒森举行的第36届世界体操锦标赛中,“李小鹏跳”——“踺子后手翻转体180度接直体前空翻转体900度”,震惊四座,这里的转体180度、 转体900度就是一个角的概念.
初中角的定义:
从一个点出发引出的两条射线构成的
几何图形(0°,360°)
“旋转”形成角
角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形.
1、角的范围
o
A
B
始边
终边
顶点
1、花样游泳中,运动员旋转的周数如何
用角度计算来表示?
2、汽车在前进和倒车中,车轮转动的角度
如何表示才比较合理?
3、工人在拧紧或拧松螺丝时,转动的角度
如何表示才比较合适?
正角:按逆时针方向旋转形成的角
负角:按顺时针方向旋转形成的角
零角:一条射线没有作任何旋转形 成的角
任意角
x
y
o
1)置角的顶点于原点
终边落在第几象限就是第几象限角
2)始边重合于x轴的非负半轴
始边
终边
A
B
o
练习
1、判断
1)、第一象限角都是锐角( )
2)、锐角都是第一象限角( )
3)、小于90°的角都是锐角( )
2、A={小于90°的角},B={第一象限角},则A∩B=( )
A、{锐角} B、{小于90°的角}
C、{第一象限角} D、以上都不对
√
×
×
D
x
y
o
300
3900=300+3600
-3300=300-3600
300= 300+0×3600
与α终边相同的角的一般形式为
α+k 3600,k ∈ Z
S={ β| β=α+k 360° ,k∈ Z}
所有与角α终边相同的角,连同角α在内,可构成一个集合
即任一与角α终边相同的角,都可以表示成角α与整数个周角的和。
反思:
终边相同的角 相等;
但相等的角,终边 相同;
终边相同的角有无数多个,
它们相差 360°的整数倍.
不一定
一定
例1 把下列各角写成α+k 3600 (00≤a<3600,k∈z)的形式,并判定它们分别是第几象限角。
–120°; (2)660°;(3)-950°08′.
∴与 角终边相同的角是 角,
(1)∵
它是第三象限的角;
解:
∴与 角终边相同的角是 角,
它是第四象限的角;
(2)∵
所以与 角终边相同的角是 ,
(3)
它是第二象限角.
变式:写出与下列终边相同的角的集合,并写出-720°~360°间角.
(1)120°;
(2)-270°;
(3)1020°
-600°, -240°,120°
(2) -630°, -270°,90°
(3) -420°, -60°,300°
终边落在坐标轴上的情形
x
y
o
00
900
1800
2700
+ k 360°
+ k 360°
+ k 360°
+ k 360°
或3600+ k 360°
例2 写出终边落在y轴上的角的集合。
解:终边落在y轴非负半轴上的角的集合为
S1={β| β=900+k 3600,k∈Z}
={β| β=900+2k·1800 ,k∈Z}
终边落在y轴非正半轴上的角的集合为
S2={β| β=2700+k 3600,k∈Z}
={β| β=900+(2k+1) ·1800 ,k∈Z}
S=S1∪S2
所以终边落在y轴上的角的集合为
={β| β=900+n 1800 ,n∈Z}
x
y
O
900+k 3600
2700+k 3600
用集合表示各象限角的集合。
第一象限角
第二象限角
第三象限角
第四象限角
例3、写出终边在直线y=x上的角的集合S,并把S中适合不等式-360°≤β<720°的元素 写出来。
x
y
O
-315°, 45°,405°
动手试试
练 1. 如图,终边落在 OA位置时的角的集合是 :
终边落在OB 位置,且在-360°~360°内的角的集合是 ;
终边落在阴影部分(含边界)的角的集合是 .
小结:
角的分类
象限角及表示
终边相同角
角的定义与表示
正角,负角,零角
终边相同角应用
判断角在第几象限
特殊终边角
在给定范围内求角
以后解决问题时要意识到任意角为前提条件
提醒:
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
