6.1一元一次方程(福建省泉州市晋江市)
文档属性
| 名称 | 6.1一元一次方程(福建省泉州市晋江市) |  | |
| 格式 | rar | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-18 19:41:00 | ||
图片预览











文档简介
(共39张PPT)
奥运
奥运话题
奥运话题
2004年夏季奥运会上,我国获得32枚金牌。其中跳水队获得6枚金牌,比射击队获得金牌数的2倍少2枚。射击队获得多少枚金牌?
跳水队
比射 击队
的 2倍 少2
枚
6=2x-2
探究新知
1+2=3
5=7-2
3+b=2b+1
4+x=7
2x-2=6
象这种用等号“=”来表示相等关系的式子,叫等式。
象这样含有未知数的等式叫做方程。
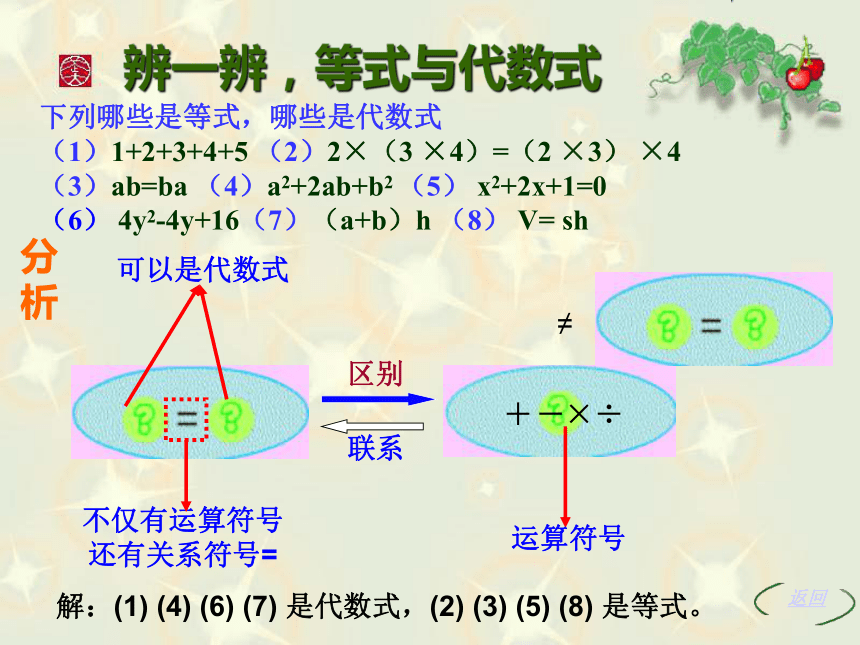
辨一辨,等式与代数式
区别
联系
不仅有运算符号还有关系符号=
运算符号
≠
可以是代数式
下列哪些是等式,哪些是代数式
(1)1+2+3+4+5 (2)2×(3 ×4)=(2 ×3) ×4
(3)ab=ba (4)a2+2ab+b2 (5) x2+2x+1=0
(6) 4y2-4y+16(7)(a+b)h (8) V= sh
分析
解:(1) (4) (6) (7) 是代数式,(2) (3) (5) (8) 是等式。
返回
选一选
下列各式中,哪些是方程?是的打 不是打
⑴ 5x=0;
⑵ 42÷6=7;
⑶ y2=4+y;
⑷ 3m+2=1-m;
⑸ 1+3x.
奥运冠军朱启南
在雅典奥运会男
子10米气步枪决
赛中最后两枪的
平均成绩为10.4
环,其中第10枪
(最后一枪)的成绩
为10.1环,问第9枪
的成绩是多少环?
练一练(根据下列问题中的条件列出方程)
设第9枪的成
绩为x环,可列
出方程:
。
练一练(根据下列问题中的条件列出方程)
练一练
国庆期间,“天一广场”搞促销
活动,小颖的姐姐买了一件衣
服,按8折销售的售价为72元,
问这件衣服的原价是多少元?
设这件衣服的原价为x元,
可列出方程 。
练一练(根据下列问题中的条件列出方程)
2008年北京奥运会
的足球分赛场---秦
皇岛市奥体中心体
育场,其足球场的
周长为344米,长和
宽之差为36米,这
个足球场的长与宽
分别是多少米?
设这个足球场的宽为x米,则长
为(x+36)米,可列出方程
。
想一想,议一议
这些方程之间有什么共同的特点
方程两边都是整式
只含有一个未知数
未知数的指数是一次
一元一次方程
选一选
下列各式中,哪些是一元一次方程?是的打 不是打
⑴ 5x=0;
⑵ y2=4+y;
⑶ 3m+2=1-m;
⑷
⑸ ;
想一想,选一选
加油!
头脑风暴
请你想出一个一元一次方程,然后写在老师发的纸上,并签上大名,再迅速将纸传给后排的同学。后排同学所写的方程,不能与前排同学的方程重复。当老师喊停时,大家停笔。看四大组中,哪组写得最多最好!(请用黑色水笔书写)
奥运冠军朱启南
在雅典奥运会男
子10米气步枪决
赛中最后两枪的
平均成绩为10.4
环,其中第10枪
(最后一枪)的成绩
为10.1环,问第9枪
的成绩是多少环?
练一练(根据下列问题中的条件列出方程)
设第9枪的成
绩为x环,可列
出方程:
。
X=
这种尝试检验的方法是解决
问题的一种重要的思想方法。
10.5 10.6 10.7 10.8 10.9
10.3
10.35
10.4
10.45
10.5
可以知道x=10.7是方程 的解
分别把0、1、2、3、4
代入下列方程,哪一个能使方程成立:
⑴ 2x-1=5
x=0时,方程的左边=___,右边=___.
x=4时,方程的左边=___,右边=___.
x=2时,方程的左边=___,右边=___.
x=3时,方程的左边=___,右边=___.
-1
5
x=1时,方程的左边=___,右边=___.
5
5
5
5
1
3
5
7
所以x=3时,能使方程成立.
x=3是方程2x-1=5的解.
方程的解的概念
使方程左右两边的
值相等的未知数的
值叫做方程的解。
⑴ x=2是方程x-10=4x的解。
⑵ x=3和x=-3都是方程
的解。
⑶ 方程12﹙x-3﹚-1=2x+3的解是x=3.
判断对错:
错
对
错
你能概括出
如何检验一个数是不是方程的解的步骤吗?
检验一个数是不是方程的解的步骤:
1.将数值代入方程左边进行计算,
2.将数值代入方程右边进行计算,
3.比较左右两边的值,若左边=右边,则是方程的解,反之,则不是.
做一做
检验下列各数是不是方程2x-3=5x-15的解
2x-3=5x-15
(1)x=6
(2)x=4
解:(1)
把x=6分别代入方程的左边和右边
左边=
2x-3
2× -3
6
=9
右边=
5x-15
5× -15
6
=15
左边
右边
x=6不是方程2x-3=5x-15的解
解:(2)
把x=4分别代入方程的左边和右边
左边=
2x-3
2× -3
=5
右边=
5x-15
5× -15
=5
左边=
右边
x=4是方程2x-3=5x-15的解
4
4
头脑体操
写 出 一 个 一 元 一 次 方程 , 使 它 的 解 是 t =- 2 ?
奥运冠军朱启南
在雅典奥运会男
子10米气步枪决
赛中最后两枪的
平均成绩为10.4
环,其中第10枪
(最后一枪)的成绩
为10.1环,问第9枪
的成绩是多少环?
练一练(根据下列问题中的条件列出方程)
设第9枪的成
绩为x环,可列
出方程:
。
X=
还可用等式的性质解一元一次方程。
数学实验室
数学实验室
等式两边都加上或减去同一个数
或同一个整式,所得的结果仍是等式。
等式两边都乘以或除以同一个不等于
零的数或式,所得的结果仍是等式。
等 式 的 性 质
例:利用等式性质解下列方程:
2x+1=5
5y=5
方程2x+1=5的变形过程:
2x+1=5
两边都减去1
2x=4
两边都除以2
x=2
两边各取走1个
两边个数都除以2
数学实验室
两边都除以5
y
y
y
y
y
5y=5
y
y=1
数学实验室
你能说出方程 3x=2x+3 是怎么变形的吗?
两边都减去2x
x=3
3x=2x+3
数学实验室
⑴ 由x+5 = y+5,得到 x = y
⑵由2x-1=4,得到2x=5
⑶由2x=1,得到x=2
⑷由3x=2x,得到3=2
判断下列变形是否正确,
为什么
对
错
对
错
用适当的数或整式填空,使得结果仍是等式,并说明依据是什么。
⑴ 如果6+x=2,那么x=___
⑵ 如果x-y=5,那么x=5+___
⑶如果
,那么-y=4-____
⑷如果
,那么x=___
-4
y
10
填空:
⑴如果2x+7=13,那么2x=13__
⑵如果5x=4x+7,那么5x____=7。
⑶如果-3x=12,那么x=___。
⑷如果2a=1.6,那么4a=___。
⑸如果-5x=5y,那么x=__。
⑹如果
,那么x=_。
-7
-4x
-4
3.2
-y
8
⑴ x+5=2
⑵ -2x=4
⑵两边都除以-2,得
=
即x=-2
解:
⑴
两边都减去5,得
x+5-5=2-5
合并同类项,得
x=-3
利用等式性质 , 解下列方程:
求方程的解,就是将
方程变形为____的形式。
x=a
1.解下列方程:
⑴ x+2=-6
⑵ -3x=3-4x
⑶
⑷ -6x=2
练一练
2. 在公元前1600年左右遗留下来的
古埃及文献中,有这样一个问题:
你能求出这个数吗?
“它的全部,它的
,和等于19”。
解:设这个数为x,根据题意,列方程得:
x+
=19
解得x=
这节课,你有什么收获,能与我们一起分享吗?
通过这节课的学习,你有那些收获,能与我们一起分享吗?
作业:
作业本
奥运
奥运话题
奥运话题
2004年夏季奥运会上,我国获得32枚金牌。其中跳水队获得6枚金牌,比射击队获得金牌数的2倍少2枚。射击队获得多少枚金牌?
跳水队
比射 击队
的 2倍 少2
枚
6=2x-2
探究新知
1+2=3
5=7-2
3+b=2b+1
4+x=7
2x-2=6
象这种用等号“=”来表示相等关系的式子,叫等式。
象这样含有未知数的等式叫做方程。
辨一辨,等式与代数式
区别
联系
不仅有运算符号还有关系符号=
运算符号
≠
可以是代数式
下列哪些是等式,哪些是代数式
(1)1+2+3+4+5 (2)2×(3 ×4)=(2 ×3) ×4
(3)ab=ba (4)a2+2ab+b2 (5) x2+2x+1=0
(6) 4y2-4y+16(7)(a+b)h (8) V= sh
分析
解:(1) (4) (6) (7) 是代数式,(2) (3) (5) (8) 是等式。
返回
选一选
下列各式中,哪些是方程?是的打 不是打
⑴ 5x=0;
⑵ 42÷6=7;
⑶ y2=4+y;
⑷ 3m+2=1-m;
⑸ 1+3x.
奥运冠军朱启南
在雅典奥运会男
子10米气步枪决
赛中最后两枪的
平均成绩为10.4
环,其中第10枪
(最后一枪)的成绩
为10.1环,问第9枪
的成绩是多少环?
练一练(根据下列问题中的条件列出方程)
设第9枪的成
绩为x环,可列
出方程:
。
练一练(根据下列问题中的条件列出方程)
练一练
国庆期间,“天一广场”搞促销
活动,小颖的姐姐买了一件衣
服,按8折销售的售价为72元,
问这件衣服的原价是多少元?
设这件衣服的原价为x元,
可列出方程 。
练一练(根据下列问题中的条件列出方程)
2008年北京奥运会
的足球分赛场---秦
皇岛市奥体中心体
育场,其足球场的
周长为344米,长和
宽之差为36米,这
个足球场的长与宽
分别是多少米?
设这个足球场的宽为x米,则长
为(x+36)米,可列出方程
。
想一想,议一议
这些方程之间有什么共同的特点
方程两边都是整式
只含有一个未知数
未知数的指数是一次
一元一次方程
选一选
下列各式中,哪些是一元一次方程?是的打 不是打
⑴ 5x=0;
⑵ y2=4+y;
⑶ 3m+2=1-m;
⑷
⑸ ;
想一想,选一选
加油!
头脑风暴
请你想出一个一元一次方程,然后写在老师发的纸上,并签上大名,再迅速将纸传给后排的同学。后排同学所写的方程,不能与前排同学的方程重复。当老师喊停时,大家停笔。看四大组中,哪组写得最多最好!(请用黑色水笔书写)
奥运冠军朱启南
在雅典奥运会男
子10米气步枪决
赛中最后两枪的
平均成绩为10.4
环,其中第10枪
(最后一枪)的成绩
为10.1环,问第9枪
的成绩是多少环?
练一练(根据下列问题中的条件列出方程)
设第9枪的成
绩为x环,可列
出方程:
。
X=
这种尝试检验的方法是解决
问题的一种重要的思想方法。
10.5 10.6 10.7 10.8 10.9
10.3
10.35
10.4
10.45
10.5
可以知道x=10.7是方程 的解
分别把0、1、2、3、4
代入下列方程,哪一个能使方程成立:
⑴ 2x-1=5
x=0时,方程的左边=___,右边=___.
x=4时,方程的左边=___,右边=___.
x=2时,方程的左边=___,右边=___.
x=3时,方程的左边=___,右边=___.
-1
5
x=1时,方程的左边=___,右边=___.
5
5
5
5
1
3
5
7
所以x=3时,能使方程成立.
x=3是方程2x-1=5的解.
方程的解的概念
使方程左右两边的
值相等的未知数的
值叫做方程的解。
⑴ x=2是方程x-10=4x的解。
⑵ x=3和x=-3都是方程
的解。
⑶ 方程12﹙x-3﹚-1=2x+3的解是x=3.
判断对错:
错
对
错
你能概括出
如何检验一个数是不是方程的解的步骤吗?
检验一个数是不是方程的解的步骤:
1.将数值代入方程左边进行计算,
2.将数值代入方程右边进行计算,
3.比较左右两边的值,若左边=右边,则是方程的解,反之,则不是.
做一做
检验下列各数是不是方程2x-3=5x-15的解
2x-3=5x-15
(1)x=6
(2)x=4
解:(1)
把x=6分别代入方程的左边和右边
左边=
2x-3
2× -3
6
=9
右边=
5x-15
5× -15
6
=15
左边
右边
x=6不是方程2x-3=5x-15的解
解:(2)
把x=4分别代入方程的左边和右边
左边=
2x-3
2× -3
=5
右边=
5x-15
5× -15
=5
左边=
右边
x=4是方程2x-3=5x-15的解
4
4
头脑体操
写 出 一 个 一 元 一 次 方程 , 使 它 的 解 是 t =- 2 ?
奥运冠军朱启南
在雅典奥运会男
子10米气步枪决
赛中最后两枪的
平均成绩为10.4
环,其中第10枪
(最后一枪)的成绩
为10.1环,问第9枪
的成绩是多少环?
练一练(根据下列问题中的条件列出方程)
设第9枪的成
绩为x环,可列
出方程:
。
X=
还可用等式的性质解一元一次方程。
数学实验室
数学实验室
等式两边都加上或减去同一个数
或同一个整式,所得的结果仍是等式。
等式两边都乘以或除以同一个不等于
零的数或式,所得的结果仍是等式。
等 式 的 性 质
例:利用等式性质解下列方程:
2x+1=5
5y=5
方程2x+1=5的变形过程:
2x+1=5
两边都减去1
2x=4
两边都除以2
x=2
两边各取走1个
两边个数都除以2
数学实验室
两边都除以5
y
y
y
y
y
5y=5
y
y=1
数学实验室
你能说出方程 3x=2x+3 是怎么变形的吗?
两边都减去2x
x=3
3x=2x+3
数学实验室
⑴ 由x+5 = y+5,得到 x = y
⑵由2x-1=4,得到2x=5
⑶由2x=1,得到x=2
⑷由3x=2x,得到3=2
判断下列变形是否正确,
为什么
对
错
对
错
用适当的数或整式填空,使得结果仍是等式,并说明依据是什么。
⑴ 如果6+x=2,那么x=___
⑵ 如果x-y=5,那么x=5+___
⑶如果
,那么-y=4-____
⑷如果
,那么x=___
-4
y
10
填空:
⑴如果2x+7=13,那么2x=13__
⑵如果5x=4x+7,那么5x____=7。
⑶如果-3x=12,那么x=___。
⑷如果2a=1.6,那么4a=___。
⑸如果-5x=5y,那么x=__。
⑹如果
,那么x=_。
-7
-4x
-4
3.2
-y
8
⑴ x+5=2
⑵ -2x=4
⑵两边都除以-2,得
=
即x=-2
解:
⑴
两边都减去5,得
x+5-5=2-5
合并同类项,得
x=-3
利用等式性质 , 解下列方程:
求方程的解,就是将
方程变形为____的形式。
x=a
1.解下列方程:
⑴ x+2=-6
⑵ -3x=3-4x
⑶
⑷ -6x=2
练一练
2. 在公元前1600年左右遗留下来的
古埃及文献中,有这样一个问题:
你能求出这个数吗?
“它的全部,它的
,和等于19”。
解:设这个数为x,根据题意,列方程得:
x+
=19
解得x=
这节课,你有什么收获,能与我们一起分享吗?
通过这节课的学习,你有那些收获,能与我们一起分享吗?
作业:
作业本
