5.3三角函数的诱导公式课件2-2023-2024学年高一上学期数学人教A版(2019)必修第一册(共19张PPT)
文档属性
| 名称 | 5.3三角函数的诱导公式课件2-2023-2024学年高一上学期数学人教A版(2019)必修第一册(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1014.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-21 09:45:11 | ||
图片预览






文档简介
(共19张PPT)
5.3三角函数的诱导公式2
诱导公式二:
诱导公式三:
诱导公式四:
sin(2kπ+α)= sinα
cos(2kπ+α)= cosα
tan(2kπ+α)= tanα
诱导公式一:
复习引入
诱导公式二:
诱导公式三:
诱导公式一:
诱导公式四:
诱导公式二:
诱导公式三:
诱导公式一:
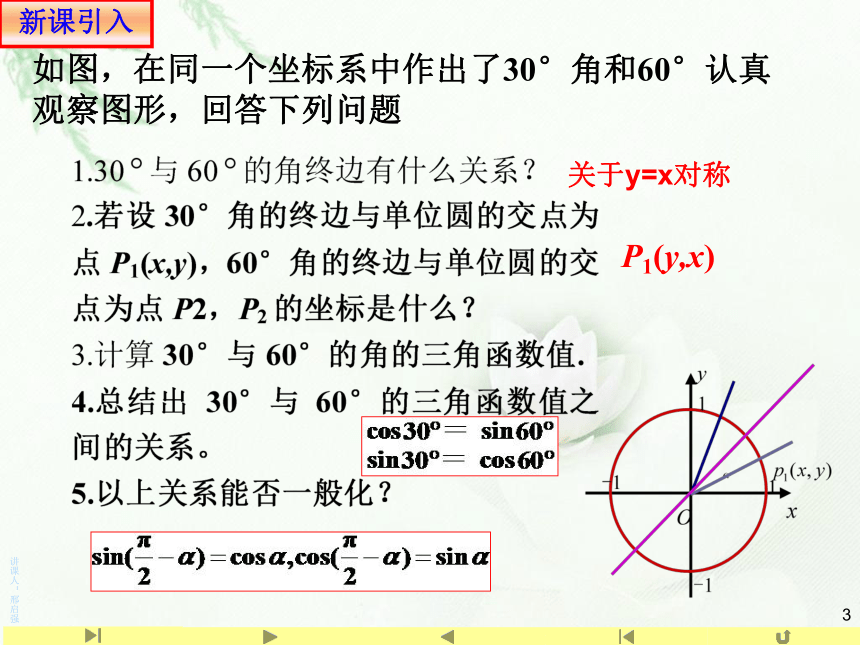
如图,在同一个坐标系中作出了30°角和60°认真观察图形,回答下列问题
新课引入
关于y=x对称
P1(y,x)
x
o
y
1
-1
1
-1
任意角 的终边与单位圆相交于点 ,角 的终边与单位圆的交于点 ,又因单位圆由正弦函数和余弦函数的定义得到:
从而得公式五:
学习新知
学习新知
角α的终边与角 终边有什么关系?关于什么对称?
学习新知
同样可得公式六:
口诀:正变余,余变正,符号象限定
公式的作用:实现正弦函数与余弦函数的转化,三角恒等变换中,起到改变函数名称的作用
学习新知
x
y
0
意义:
学习新知
诱导公式的记忆口诀 :
奇变偶不变,符号看象限,
象限怎么判,把α锐角看
学习新知
任意角的三角函数
相应正角的三角函数
角的三角函数
锐角的三角函数
三角函数值
求任意角的三角函数值的步骤:
学习新知
典型例题
典型例题
【规律总结】从整体把握角与角之间的相互关系及其恒等变形是本题的解题要点,把未知角化为已知角,是三角变换中的一个重要策略.
=1
典型例题
典型例题
典型例题
典型例题
思考题:
1.设
其中a,b,α,β都是非零实数,
若f(2005)= -1,则f(2006)等于( )
-1 B. 0 C. 1 D. 2
巩固练习
C
2.思考题
若 ,则
深化练习
(1)求任意角的三角函数式的一般程序:负(角)变正(角)→大(角)变小(角)→(一直)变到 ~ 之间.
(2)变角是有一定技巧的,如 可写成 ,
也可以写成 不同表达方法,决定着使用不同
的诱导公式.
(3)凑角方法也体现出很大技巧。如,已知角“ ”,
求未知角“ ”,可把 改写成 .
课堂小结
5.3三角函数的诱导公式2
诱导公式二:
诱导公式三:
诱导公式四:
sin(2kπ+α)= sinα
cos(2kπ+α)= cosα
tan(2kπ+α)= tanα
诱导公式一:
复习引入
诱导公式二:
诱导公式三:
诱导公式一:
诱导公式四:
诱导公式二:
诱导公式三:
诱导公式一:
如图,在同一个坐标系中作出了30°角和60°认真观察图形,回答下列问题
新课引入
关于y=x对称
P1(y,x)
x
o
y
1
-1
1
-1
任意角 的终边与单位圆相交于点 ,角 的终边与单位圆的交于点 ,又因单位圆由正弦函数和余弦函数的定义得到:
从而得公式五:
学习新知
学习新知
角α的终边与角 终边有什么关系?关于什么对称?
学习新知
同样可得公式六:
口诀:正变余,余变正,符号象限定
公式的作用:实现正弦函数与余弦函数的转化,三角恒等变换中,起到改变函数名称的作用
学习新知
x
y
0
意义:
学习新知
诱导公式的记忆口诀 :
奇变偶不变,符号看象限,
象限怎么判,把α锐角看
学习新知
任意角的三角函数
相应正角的三角函数
角的三角函数
锐角的三角函数
三角函数值
求任意角的三角函数值的步骤:
学习新知
典型例题
典型例题
【规律总结】从整体把握角与角之间的相互关系及其恒等变形是本题的解题要点,把未知角化为已知角,是三角变换中的一个重要策略.
=1
典型例题
典型例题
典型例题
典型例题
思考题:
1.设
其中a,b,α,β都是非零实数,
若f(2005)= -1,则f(2006)等于( )
-1 B. 0 C. 1 D. 2
巩固练习
C
2.思考题
若 ,则
深化练习
(1)求任意角的三角函数式的一般程序:负(角)变正(角)→大(角)变小(角)→(一直)变到 ~ 之间.
(2)变角是有一定技巧的,如 可写成 ,
也可以写成 不同表达方法,决定着使用不同
的诱导公式.
(3)凑角方法也体现出很大技巧。如,已知角“ ”,
求未知角“ ”,可把 改写成 .
课堂小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
