人教版数学八年级上册 12.2 三角形全等的判定 第1课时 SSS 导学案(含答案)
文档属性
| 名称 | 人教版数学八年级上册 12.2 三角形全等的判定 第1课时 SSS 导学案(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 73.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-01 10:42:48 | ||
图片预览


文档简介
第十二章 全等三角形
第1课时 边边边
学习目标
1.能自己试验探索出判定三角形全等的条件:边边边公理.
2.会应用判定方法SSS进行简单的推理判定两个三角形全等.
3.会作一个角等于已知角.
学习策略
1.通过画符合条件的三角形,理解三角形全等的判定;
2.牢记三角形全等的判定方法.
学习过程
一、复习回顾:
1.上节课我们学习了全等三角形和全等三角形的性质,请同学们回顾其内容;
2.如何判断两个三角形能够完全重合?
二.新课学习:
知识点:三角形全等的判定方法1:“边边边”
阅读课本本课时内容,解决下列问题.
1.判定两个三角形全等需要几个条件 都是哪些
【答案】六个;三条边对应相等,三个角对应相等
2.“满足上述六个条件中的一个或两个”有哪几种情况 请列举出来并完成课本“探究1”.
【答案】有五种情况:①一个角对应相等;②一条边对应相等;③两个角对应相等;④两条边对应相等;⑤一个角对应相等,一条边对应相等
3.“满足上述六个条件中的三个”有哪几种情况,请列举出来.
【答案】有四种情况:①三条边对应相等;②三个角对应相等;③两条边对应相等,一个角对应相等;④两个角对应相等,一条边对应相等
4.已知一个△ABC的三条边分别为AB=4 cm,AC=5 cm,BC=7 cm,请用课本中的方法作出这个三角形.把你画的三角形与其他同学画的三角形进行比较,全等吗
【答案】作法:①画AB=4 cm;②分别以A,B为圆心,以5 cm,7 cm为半径画弧,两弧相交于点C;③连接线段AC,BC;全等
综之:三边分别相等的两个三角形全等(简写:“ ”或“ ”).
【答案】边边边;SSS
三.尝试应用:
例1.两个全等的三角形纸板从重合状态下向右平移一段距离,可得下图,若已知AB=DE,BE=CF,DF=AC,△ABC和△DEF全等吗 说明理由.
解:BC与EF相等,
理由:因为BE=CF,
所以BE+EC=CF+EC,即:CB=EF;
因为在△ABC和△DEF中,,
所以△ABC≌△DEF(SSS).
变式:根据已知条件,你还能得到哪些正确的结论
答:∠A=∠D , ∠B=∠DEF, ∠F=∠ACB ,AB∥DE,AC∥DF 等
例2 已知:∠AOB,
求作:∠A′O′B′,使:∠A′O′B′=∠AOB
解:①作射线O′A′,
②以点O为圆心,以任意长为半径作弧,交OA于C,交OB于D,
③以点O′为圆心,以OC长为半径作弧,交O′A′于C′,
④以点C′圆心,以CD为半径作弧,交③中所画弧于D′,
⑤经过点D′作射线O′B′,∠A′O′B′就是所求的角
四.自主总结:
本节课我们探索得到了三角形全等的条件,发现了证明三角形全等的一个规律SSS.并利用它可以证明简单的三角形全等问题,注意要规范几何语言.
另一个是尺规作图:作一个角等于已知角,原理是SSS。
五.达标测试
一、选择题
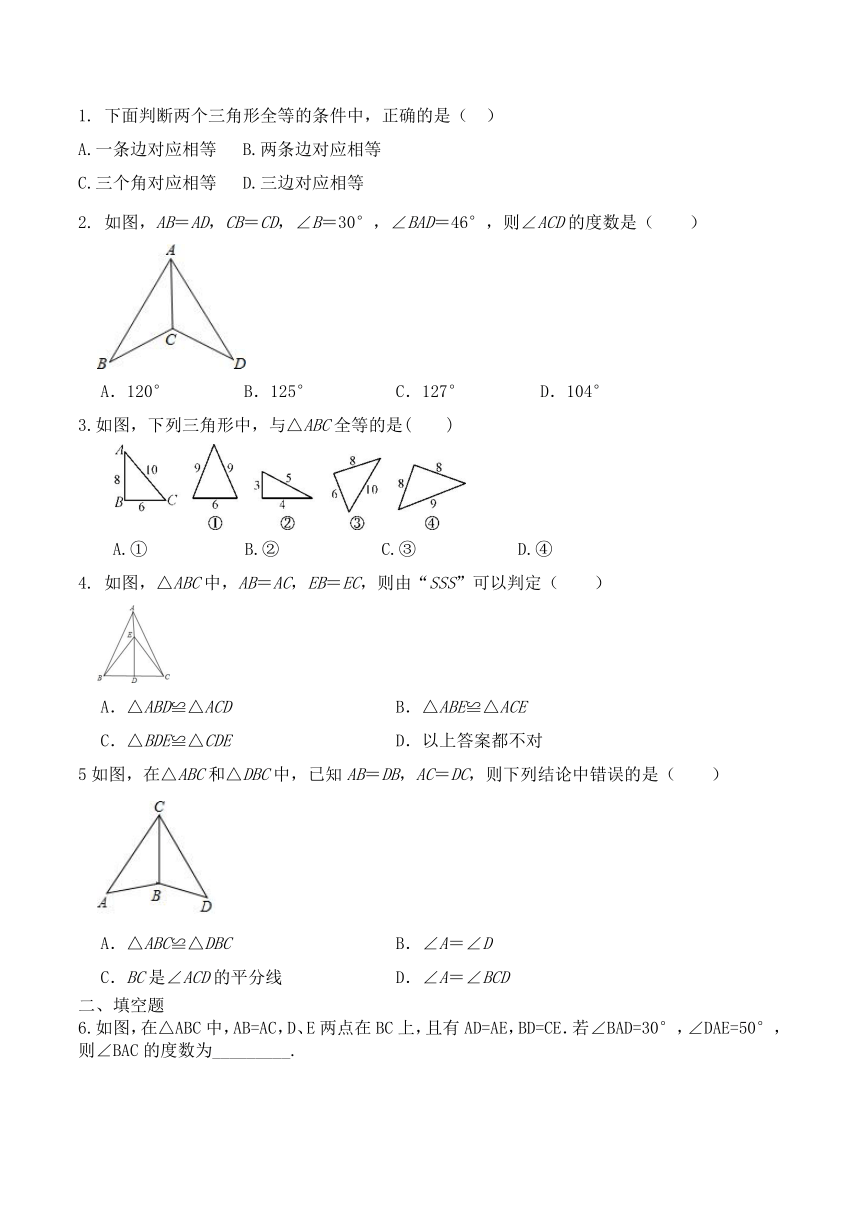
1. 下面判断两个三角形全等的条件中,正确的是( )
A.一条边对应相等 B.两条边对应相等
C.三个角对应相等 D.三边对应相等
2. 如图,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是( )
A.120° B.125° C.127° D.104°
3.如图,下列三角形中,与△ABC全等的是( )
A.① B.② C.③ D.④
4. 如图,△ABC中,AB=AC,EB=EC,则由“SSS”可以判定( )
A.△ABD≌△ACD B.△ABE≌△ACE
C.△BDE≌△CDE D.以上答案都不对
5如图,在△ABC和△DBC中,已知AB=DB,AC=DC,则下列结论中错误的是( )
A.△ABC≌△DBC B.∠A=∠D
C.BC是∠ACD的平分线 D.∠A=∠BCD
二、填空题
6.如图,在△ABC中,AB=AC,D、E两点在BC上,且有AD=AE,BD=CE.若∠BAD=30°,∠DAE=50°,则∠BAC的度数为_________.
7. 如图,AB=AC,BE=CD,要使△ABE≌△ACD,依据SSS,则还需添加条件 .
8.如图,每个小方格都是边长为1的小正方形,△ABC是格点三角形(即顶点恰好是小正方形的顶点),在图中与△ABC不重叠且有一条公共边的全等的所有格点三角形有______个.
三、解答题
9.如图,C是AB的中点,AD=CE,CD=BE,求证△ACD≌△CBE
10. (1)班同学上数学活动课,利用角尺平分一个角(如图所示).设计了如下方案:
(Ⅰ)∠AOB是一个任意角,将角尺的直角顶点P介于射线OA、OB之间,移动角尺使角尺两边相同的刻度与M、N重合,即PM=PN,过角尺顶点P的射线OP就是∠AOB的平分线.
(Ⅱ)∠AOB是一个任意角,在边OA、OB上分别取OM=ON,将角尺的直角顶点P介于射线OA、OB之间,移动角尺使角尺两边相同的刻度与M、N重合,即PM=PN,过角尺顶点P的射线OP就是∠AOB的平分线.
(1)方案(Ⅰ)、方案(Ⅱ)是否可行?若可行,请证明;若不可行,请说明理由;
(2)在方案(Ⅰ)PM=PN的情况下,继续移动角尺,同时使PM⊥OA,PN⊥OB.此方案是否可行?请说明理由.
参考答案
1. D解析:判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.故只有D符合SSS能判定三角形全等.故选:D.
2. C解析:因为在△ABC和△ADC中
所以△ABC≌△ADC,
所以∠B=∠D=30°,∠BAC=∠DAC=∠BAD=×46°=23°,
所以∠ACD=180°﹣∠D﹣∠DAC=180°﹣30°﹣23°=127°,故选:C.
3. C解析:因为三角形要全等对应边必须相等,所以只有③与△ABC的各边都相等,只有③正确,故选C.
4. B解析:因为AB=AC,EB=EC,AE=AE,
所以△ABE≌△ACE(SSS).故选:B.
5. D解析:在△ABC与△DBC中,,
所以△ABC≌△DBC,
所以∠A=∠D,∠ACB=∠DCB,
所以BC是∠ACD的平分线,故选:D.
6. C解析:因为△ABC中,AB=AC,AD=AE,BD=CE,
所以△ABD≌△ACE,
所以∠BAD=∠CAE=30°
所以∠BAC=∠BAD+∠DAE+∠CAE=30°+50°+30°=110°
7. 解析:因为AB=AC,BE=CD,要使△ABE≌△ACD,依据SSS,所以还需添加条件AE=AD即可.
8. B解析:如图所示,以BC为公共边的三角形有3个,以AB为公共边的三角形有0个,以AC为公共边的三角形有1个,
所以与△ABC不重各且有一条公共边的全等的格点三角形的个数是4,
故选:B.
9.因为C是AB的中点,所以AC=CB.
在△ACD和△CBE中,
AC=CB,AD=CE,CD=BE,所以△ACD≌△CBE(SSS).
10. 解:(1)方案(Ⅰ)不可行.缺少证明三角形全等的条件,
因为只有OP=OP,PM=PN不能判断△OPM≌△OPN;
所以就不能判定OP就是∠AOB的平分线;
方案(Ⅱ)可行.
证明:在△OPM和△OPN中,,
所以△OPM≌△OPN(SSS),
所以∠AOP=∠BOP(全等三角形对应角相等);
所以OP就是∠AOB的平分线.
(2)当∠AOB是直角时,此方案可行;
因为四边形内角和为360°,∠OMP=∠ONP=90°,∠MPN=90°,
所以∠AOB=90°,
因为PM=PN,
所以OP为∠AOB的平分线.(到角两边距离相等的点在这个角的角平分线上),
当∠AOB不为直角时,此方案不可行;
因为∠AOB必为90°,如果不是90°,则不能找到同时使PM⊥OA,PN⊥OB的点P的位置.
第1课时 边边边
学习目标
1.能自己试验探索出判定三角形全等的条件:边边边公理.
2.会应用判定方法SSS进行简单的推理判定两个三角形全等.
3.会作一个角等于已知角.
学习策略
1.通过画符合条件的三角形,理解三角形全等的判定;
2.牢记三角形全等的判定方法.
学习过程
一、复习回顾:
1.上节课我们学习了全等三角形和全等三角形的性质,请同学们回顾其内容;
2.如何判断两个三角形能够完全重合?
二.新课学习:
知识点:三角形全等的判定方法1:“边边边”
阅读课本本课时内容,解决下列问题.
1.判定两个三角形全等需要几个条件 都是哪些
【答案】六个;三条边对应相等,三个角对应相等
2.“满足上述六个条件中的一个或两个”有哪几种情况 请列举出来并完成课本“探究1”.
【答案】有五种情况:①一个角对应相等;②一条边对应相等;③两个角对应相等;④两条边对应相等;⑤一个角对应相等,一条边对应相等
3.“满足上述六个条件中的三个”有哪几种情况,请列举出来.
【答案】有四种情况:①三条边对应相等;②三个角对应相等;③两条边对应相等,一个角对应相等;④两个角对应相等,一条边对应相等
4.已知一个△ABC的三条边分别为AB=4 cm,AC=5 cm,BC=7 cm,请用课本中的方法作出这个三角形.把你画的三角形与其他同学画的三角形进行比较,全等吗
【答案】作法:①画AB=4 cm;②分别以A,B为圆心,以5 cm,7 cm为半径画弧,两弧相交于点C;③连接线段AC,BC;全等
综之:三边分别相等的两个三角形全等(简写:“ ”或“ ”).
【答案】边边边;SSS
三.尝试应用:
例1.两个全等的三角形纸板从重合状态下向右平移一段距离,可得下图,若已知AB=DE,BE=CF,DF=AC,△ABC和△DEF全等吗 说明理由.
解:BC与EF相等,
理由:因为BE=CF,
所以BE+EC=CF+EC,即:CB=EF;
因为在△ABC和△DEF中,,
所以△ABC≌△DEF(SSS).
变式:根据已知条件,你还能得到哪些正确的结论
答:∠A=∠D , ∠B=∠DEF, ∠F=∠ACB ,AB∥DE,AC∥DF 等
例2 已知:∠AOB,
求作:∠A′O′B′,使:∠A′O′B′=∠AOB
解:①作射线O′A′,
②以点O为圆心,以任意长为半径作弧,交OA于C,交OB于D,
③以点O′为圆心,以OC长为半径作弧,交O′A′于C′,
④以点C′圆心,以CD为半径作弧,交③中所画弧于D′,
⑤经过点D′作射线O′B′,∠A′O′B′就是所求的角
四.自主总结:
本节课我们探索得到了三角形全等的条件,发现了证明三角形全等的一个规律SSS.并利用它可以证明简单的三角形全等问题,注意要规范几何语言.
另一个是尺规作图:作一个角等于已知角,原理是SSS。
五.达标测试
一、选择题
1. 下面判断两个三角形全等的条件中,正确的是( )
A.一条边对应相等 B.两条边对应相等
C.三个角对应相等 D.三边对应相等
2. 如图,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是( )
A.120° B.125° C.127° D.104°
3.如图,下列三角形中,与△ABC全等的是( )
A.① B.② C.③ D.④
4. 如图,△ABC中,AB=AC,EB=EC,则由“SSS”可以判定( )
A.△ABD≌△ACD B.△ABE≌△ACE
C.△BDE≌△CDE D.以上答案都不对
5如图,在△ABC和△DBC中,已知AB=DB,AC=DC,则下列结论中错误的是( )
A.△ABC≌△DBC B.∠A=∠D
C.BC是∠ACD的平分线 D.∠A=∠BCD
二、填空题
6.如图,在△ABC中,AB=AC,D、E两点在BC上,且有AD=AE,BD=CE.若∠BAD=30°,∠DAE=50°,则∠BAC的度数为_________.
7. 如图,AB=AC,BE=CD,要使△ABE≌△ACD,依据SSS,则还需添加条件 .
8.如图,每个小方格都是边长为1的小正方形,△ABC是格点三角形(即顶点恰好是小正方形的顶点),在图中与△ABC不重叠且有一条公共边的全等的所有格点三角形有______个.
三、解答题
9.如图,C是AB的中点,AD=CE,CD=BE,求证△ACD≌△CBE
10. (1)班同学上数学活动课,利用角尺平分一个角(如图所示).设计了如下方案:
(Ⅰ)∠AOB是一个任意角,将角尺的直角顶点P介于射线OA、OB之间,移动角尺使角尺两边相同的刻度与M、N重合,即PM=PN,过角尺顶点P的射线OP就是∠AOB的平分线.
(Ⅱ)∠AOB是一个任意角,在边OA、OB上分别取OM=ON,将角尺的直角顶点P介于射线OA、OB之间,移动角尺使角尺两边相同的刻度与M、N重合,即PM=PN,过角尺顶点P的射线OP就是∠AOB的平分线.
(1)方案(Ⅰ)、方案(Ⅱ)是否可行?若可行,请证明;若不可行,请说明理由;
(2)在方案(Ⅰ)PM=PN的情况下,继续移动角尺,同时使PM⊥OA,PN⊥OB.此方案是否可行?请说明理由.
参考答案
1. D解析:判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.故只有D符合SSS能判定三角形全等.故选:D.
2. C解析:因为在△ABC和△ADC中
所以△ABC≌△ADC,
所以∠B=∠D=30°,∠BAC=∠DAC=∠BAD=×46°=23°,
所以∠ACD=180°﹣∠D﹣∠DAC=180°﹣30°﹣23°=127°,故选:C.
3. C解析:因为三角形要全等对应边必须相等,所以只有③与△ABC的各边都相等,只有③正确,故选C.
4. B解析:因为AB=AC,EB=EC,AE=AE,
所以△ABE≌△ACE(SSS).故选:B.
5. D解析:在△ABC与△DBC中,,
所以△ABC≌△DBC,
所以∠A=∠D,∠ACB=∠DCB,
所以BC是∠ACD的平分线,故选:D.
6. C解析:因为△ABC中,AB=AC,AD=AE,BD=CE,
所以△ABD≌△ACE,
所以∠BAD=∠CAE=30°
所以∠BAC=∠BAD+∠DAE+∠CAE=30°+50°+30°=110°
7. 解析:因为AB=AC,BE=CD,要使△ABE≌△ACD,依据SSS,所以还需添加条件AE=AD即可.
8. B解析:如图所示,以BC为公共边的三角形有3个,以AB为公共边的三角形有0个,以AC为公共边的三角形有1个,
所以与△ABC不重各且有一条公共边的全等的格点三角形的个数是4,
故选:B.
9.因为C是AB的中点,所以AC=CB.
在△ACD和△CBE中,
AC=CB,AD=CE,CD=BE,所以△ACD≌△CBE(SSS).
10. 解:(1)方案(Ⅰ)不可行.缺少证明三角形全等的条件,
因为只有OP=OP,PM=PN不能判断△OPM≌△OPN;
所以就不能判定OP就是∠AOB的平分线;
方案(Ⅱ)可行.
证明:在△OPM和△OPN中,,
所以△OPM≌△OPN(SSS),
所以∠AOP=∠BOP(全等三角形对应角相等);
所以OP就是∠AOB的平分线.
(2)当∠AOB是直角时,此方案可行;
因为四边形内角和为360°,∠OMP=∠ONP=90°,∠MPN=90°,
所以∠AOB=90°,
因为PM=PN,
所以OP为∠AOB的平分线.(到角两边距离相等的点在这个角的角平分线上),
当∠AOB不为直角时,此方案不可行;
因为∠AOB必为90°,如果不是90°,则不能找到同时使PM⊥OA,PN⊥OB的点P的位置.
