青岛版数学八年级上册 2.6.1等腰三角形 课件(共22张PPT)
文档属性
| 名称 | 青岛版数学八年级上册 2.6.1等腰三角形 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 761.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-21 00:00:00 | ||
图片预览




文档简介
(共22张PPT)
等腰三角形第1课时
等腰三角形的两个底角相等。
△ABC中,AB=AC
∠B= C
分析:1.如何证明两个角相等?
2.如何构造两个全等的三角形?
猜想1
A
B
C
D
猜想与论证
已知:
求证:
A
B
C
则有∠1=∠2
D
1
2
在△ABD和△ACD中
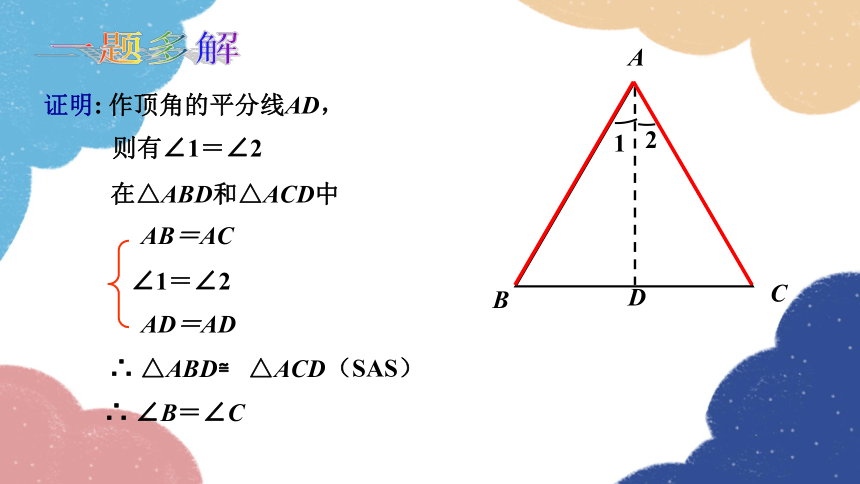
证明: 作顶角的平分线AD,
AB=AC
∠1=∠2
AD=AD
∴ △ABD≌ △ACD
(SAS)
∴ ∠B=∠C
一题多解
A
B
C
则有 BD=CD
D
在△ABD和△ACD中
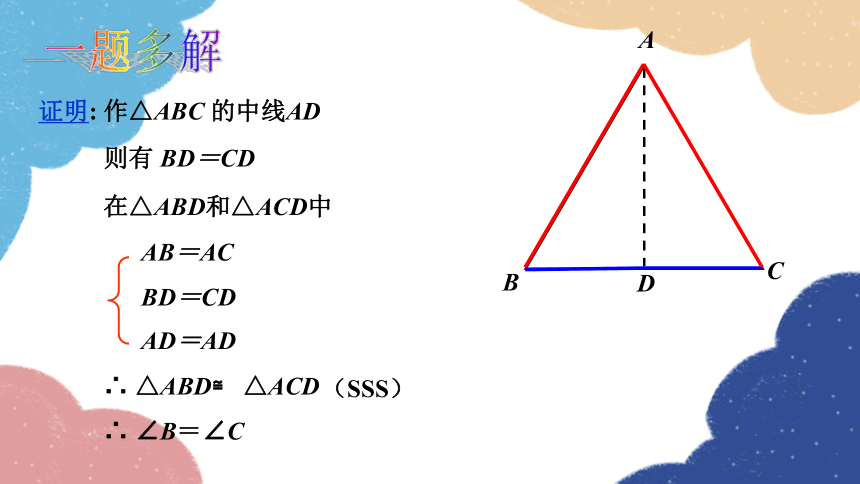
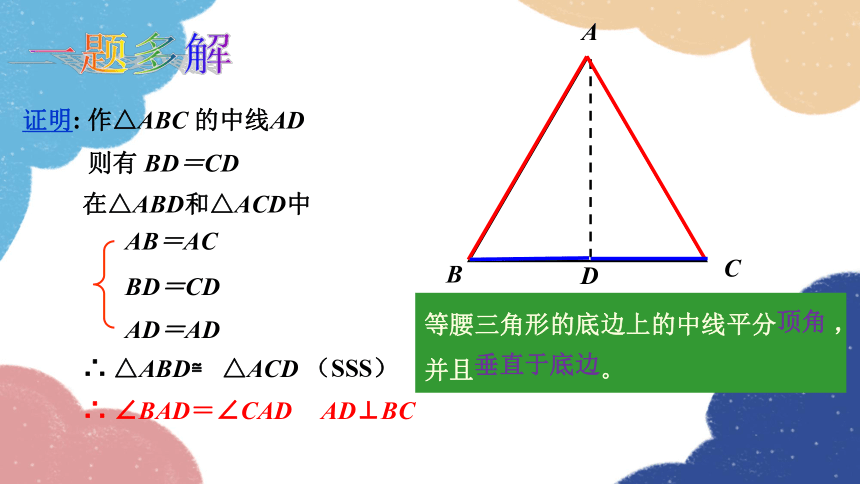
证明: 作△ABC 的中线AD
AB=AC
BD=CD
AD=AD
∴ △ABD≌ △ACD
(SSS)
∴ ∠B=∠C
一题多解
A
B
C
则有 ∠ADB=∠ADC =90
D
在Rt△ABD和Rt△ACD中
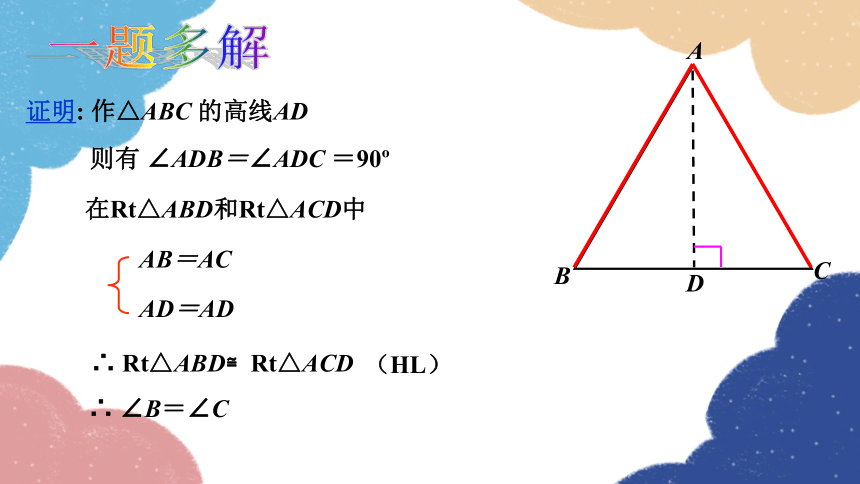
证明: 作△ABC 的高线AD
AB=AC
AD=AD
∴ Rt△ABD≌Rt△ACD
(HL)
∴ ∠B=∠C
一题多解
A
B
C
则有∠1=∠2
D
1
2
在△ABD和△ACD中
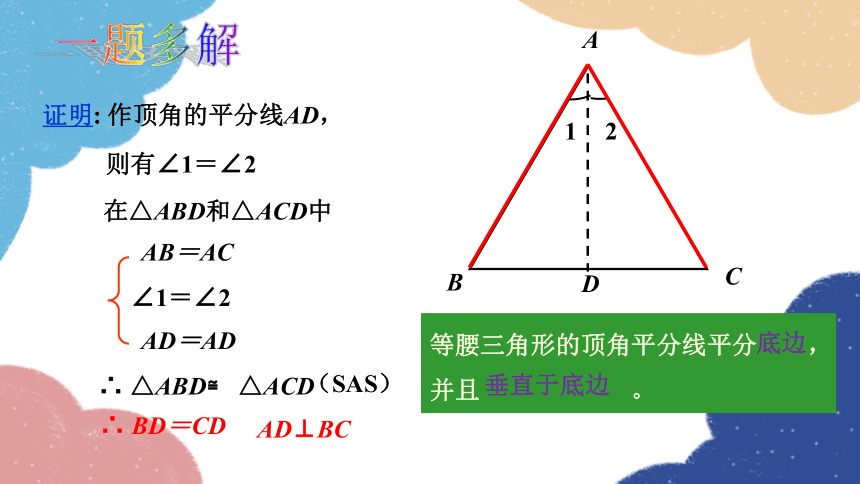
证明: 作顶角的平分线AD,
AB=AC
∠1=∠2
AD=AD
∴ △ABD≌ △ACD
(SAS)
∴ BD=CD
一题多解
AD⊥BC
等腰三角形的顶角平分线平分 ,并且 。
底边
垂直于底边
A
B
C
则有 BD=CD
D
在△ABD和△ACD中
证明: 作△ABC 的中线AD
AB=AC
BD=CD
AD=AD
∴ △ABD≌ △ACD
(SSS)
∴ ∠BAD=∠CAD
一题多解
AD⊥BC
等腰三角形的底边上的中线平分 ,并且 。
顶角
垂直于底边
A
B
C
则有 ∠ADB=∠ADC =90
D
在Rt△ABD和Rt△ACD中
证明: 作△ABC 的高线AD
AB=AC
AD=AD
∴ Rt△ABD≌Rt△ACD
(HL)
∴ ∠BAD=∠CAD
一题多解
∴ BD=CD
等腰三角形的底边上的高平分顶角,
并且平分底边。
推论:
等边三角形的三个内角相等,每一个内角都等于60°.
在三角形ABC中, AB=AC,
1、∵ AB=AC AD是顶角平分线
∴ ⊥ , = .
2、∵ AB=AC AD是底边上的高,
∴ = , ∠ =∠ .
3、∵ AB=AC AD是底边上的中线
∴ ⊥ , = .
∠BAD
∠CAD
BD
CD
BAD
AD
BC
CAD
AD
BC
BD
CD
巩固练习
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.(三线合一)
几何语言:
变式习题
1、在等腰△ABC中,AB =AC, ∠A = 50°, 则∠B =_____,∠C=______.
65°
65°
2、在等腰△ABC中, ∠A = 100°, 则∠B =_____,∠C=______.
40°
40°
3、在等腰△ABC中, ∠A = 40°,
则∠B =__________________.
70°或100°或40°
如图,是西安半坡博物馆屋顶的截面图,已经知道它的两边AB和AC是相等的.建筑工人师傅对这个建筑物做出了如下判断:
①工人师傅在测量了∠B为35°以后,并没有测量∠C ,就说∠C 的度数也是35°。
实际应用
解:①工人师傅的说法正确.
理由:
∵AB=AC
∴∠C =∠B=35°
(等边对等角)
A
C
B
D
实际应用
解:②工人师傅的说法正确.
理由:∵AB=AC BD=CD
∴AD⊥BC
(三线合一)
A
C
B
D
②工人师傅要加固屋顶,他们通过测量找到了横梁BC的中点D,然后在AD两点之间钉上一根木桩,他们认为木桩是垂直横梁的。
例1 已知,如图,在△ABC中,AB=AC, ∠BAC=120°,点D,E是
底边上两点,且BD=AD,CE=AE,求∠DAE的度数.
解:∵AB=AC,(已知)
∴∠B=∠C(等边对等角)
∴∠B=∠C=
又∵BD=AD,(已知)
∴∠BAD=∠B=30°,(等边对等角)
同理∠CAE=∠C=30°,
∴∠DAE=∠BAC-∠BAD-∠CAE
=120°-30°-30°=60°.
例题
例2 已知,如图,在△ABC中,AB=AC, 点D是在AC上,
且BD=BC=AD,求∠A和∠C的度数.
解:∵AB=AC, BD=BC=AD,(已知)
∴∠ABC=∠C=∠BDC ,
∠A=∠ABD,(等边对等角)
设∠A的度数为x,
则∠BDC=∠A+∠ABD=2x
(三角形的一个外角等于与它不相邻的两个内角的和)
∵∠ABC=∠C=∠BDC=2x,(等式性质)
∴x+2x+2x=180°,(三角形的三个内角和等于180°)
则x=36°.
∴∠A =36°,∠C =72°.
例3 求证:斜边和一条直角边对应相等的两个直角三角形全等.
已知:如图,在Rt△ABC 和Rt△A'B'C'中,
∠C=∠C'=90°,AB= A'B',AC= A'C'.
求证:Rt△ABC≌Rt△A'B'C'.
证明:在平面内移动Rt△ABC 和Rt△A'B'C',使点A和点A',点C和点C'重合,点B和点B'在AC的两侧。如图(2)所示.
∠BCB'=90°+90°=180°(等式性质)
∴B,C,B'三点在一条直线上(平角的定义)
在ABB'中,∵AB= A'B',(已知)
∴∠B=∠B',(等边对等角)
在Rt△ABC 和Rt△A'B'C'中,
∵
∴Rt△ABC≌Rt△A'B'C'.(AAS)
等腰三角形是轴对称图形
等腰三角形的两个底角相等,简称“等边对等角”
等腰三角形的顶角平分线、底边上的中线、和底边上的高互相重合,
简称“三线合 一”
等腰三角形
等腰三角形的有关概念
本节课你有什么收获?
推论:等边三角形的三个内角相等,
每一个内角都等于60°.
作业
教材练习题
等腰三角形第1课时
等腰三角形的两个底角相等。
△ABC中,AB=AC
∠B= C
分析:1.如何证明两个角相等?
2.如何构造两个全等的三角形?
猜想1
A
B
C
D
猜想与论证
已知:
求证:
A
B
C
则有∠1=∠2
D
1
2
在△ABD和△ACD中
证明: 作顶角的平分线AD,
AB=AC
∠1=∠2
AD=AD
∴ △ABD≌ △ACD
(SAS)
∴ ∠B=∠C
一题多解
A
B
C
则有 BD=CD
D
在△ABD和△ACD中
证明: 作△ABC 的中线AD
AB=AC
BD=CD
AD=AD
∴ △ABD≌ △ACD
(SSS)
∴ ∠B=∠C
一题多解
A
B
C
则有 ∠ADB=∠ADC =90
D
在Rt△ABD和Rt△ACD中
证明: 作△ABC 的高线AD
AB=AC
AD=AD
∴ Rt△ABD≌Rt△ACD
(HL)
∴ ∠B=∠C
一题多解
A
B
C
则有∠1=∠2
D
1
2
在△ABD和△ACD中
证明: 作顶角的平分线AD,
AB=AC
∠1=∠2
AD=AD
∴ △ABD≌ △ACD
(SAS)
∴ BD=CD
一题多解
AD⊥BC
等腰三角形的顶角平分线平分 ,并且 。
底边
垂直于底边
A
B
C
则有 BD=CD
D
在△ABD和△ACD中
证明: 作△ABC 的中线AD
AB=AC
BD=CD
AD=AD
∴ △ABD≌ △ACD
(SSS)
∴ ∠BAD=∠CAD
一题多解
AD⊥BC
等腰三角形的底边上的中线平分 ,并且 。
顶角
垂直于底边
A
B
C
则有 ∠ADB=∠ADC =90
D
在Rt△ABD和Rt△ACD中
证明: 作△ABC 的高线AD
AB=AC
AD=AD
∴ Rt△ABD≌Rt△ACD
(HL)
∴ ∠BAD=∠CAD
一题多解
∴ BD=CD
等腰三角形的底边上的高平分顶角,
并且平分底边。
推论:
等边三角形的三个内角相等,每一个内角都等于60°.
在三角形ABC中, AB=AC,
1、∵ AB=AC AD是顶角平分线
∴ ⊥ , = .
2、∵ AB=AC AD是底边上的高,
∴ = , ∠ =∠ .
3、∵ AB=AC AD是底边上的中线
∴ ⊥ , = .
∠BAD
∠CAD
BD
CD
BAD
AD
BC
CAD
AD
BC
BD
CD
巩固练习
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.(三线合一)
几何语言:
变式习题
1、在等腰△ABC中,AB =AC, ∠A = 50°, 则∠B =_____,∠C=______.
65°
65°
2、在等腰△ABC中, ∠A = 100°, 则∠B =_____,∠C=______.
40°
40°
3、在等腰△ABC中, ∠A = 40°,
则∠B =__________________.
70°或100°或40°
如图,是西安半坡博物馆屋顶的截面图,已经知道它的两边AB和AC是相等的.建筑工人师傅对这个建筑物做出了如下判断:
①工人师傅在测量了∠B为35°以后,并没有测量∠C ,就说∠C 的度数也是35°。
实际应用
解:①工人师傅的说法正确.
理由:
∵AB=AC
∴∠C =∠B=35°
(等边对等角)
A
C
B
D
实际应用
解:②工人师傅的说法正确.
理由:∵AB=AC BD=CD
∴AD⊥BC
(三线合一)
A
C
B
D
②工人师傅要加固屋顶,他们通过测量找到了横梁BC的中点D,然后在AD两点之间钉上一根木桩,他们认为木桩是垂直横梁的。
例1 已知,如图,在△ABC中,AB=AC, ∠BAC=120°,点D,E是
底边上两点,且BD=AD,CE=AE,求∠DAE的度数.
解:∵AB=AC,(已知)
∴∠B=∠C(等边对等角)
∴∠B=∠C=
又∵BD=AD,(已知)
∴∠BAD=∠B=30°,(等边对等角)
同理∠CAE=∠C=30°,
∴∠DAE=∠BAC-∠BAD-∠CAE
=120°-30°-30°=60°.
例题
例2 已知,如图,在△ABC中,AB=AC, 点D是在AC上,
且BD=BC=AD,求∠A和∠C的度数.
解:∵AB=AC, BD=BC=AD,(已知)
∴∠ABC=∠C=∠BDC ,
∠A=∠ABD,(等边对等角)
设∠A的度数为x,
则∠BDC=∠A+∠ABD=2x
(三角形的一个外角等于与它不相邻的两个内角的和)
∵∠ABC=∠C=∠BDC=2x,(等式性质)
∴x+2x+2x=180°,(三角形的三个内角和等于180°)
则x=36°.
∴∠A =36°,∠C =72°.
例3 求证:斜边和一条直角边对应相等的两个直角三角形全等.
已知:如图,在Rt△ABC 和Rt△A'B'C'中,
∠C=∠C'=90°,AB= A'B',AC= A'C'.
求证:Rt△ABC≌Rt△A'B'C'.
证明:在平面内移动Rt△ABC 和Rt△A'B'C',使点A和点A',点C和点C'重合,点B和点B'在AC的两侧。如图(2)所示.
∠BCB'=90°+90°=180°(等式性质)
∴B,C,B'三点在一条直线上(平角的定义)
在ABB'中,∵AB= A'B',(已知)
∴∠B=∠B',(等边对等角)
在Rt△ABC 和Rt△A'B'C'中,
∵
∴Rt△ABC≌Rt△A'B'C'.(AAS)
等腰三角形是轴对称图形
等腰三角形的两个底角相等,简称“等边对等角”
等腰三角形的顶角平分线、底边上的中线、和底边上的高互相重合,
简称“三线合 一”
等腰三角形
等腰三角形的有关概念
本节课你有什么收获?
推论:等边三角形的三个内角相等,
每一个内角都等于60°.
作业
教材练习题
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
