垂直于弦的直径(2)(浙江省台州市玉环县)
文档属性
| 名称 | 垂直于弦的直径(2)(浙江省台州市玉环县) |

|
|
| 格式 | rar | ||
| 文件大小 | 7.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-18 00:00:00 | ||
图片预览



文档简介
课件28张PPT。24.1.2垂直于弦的直径(2)温故知新1.上节课我们学了那些知识点?1.圆是轴对称图形,经过圆心的每一条直线都是它们的对称轴2.垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
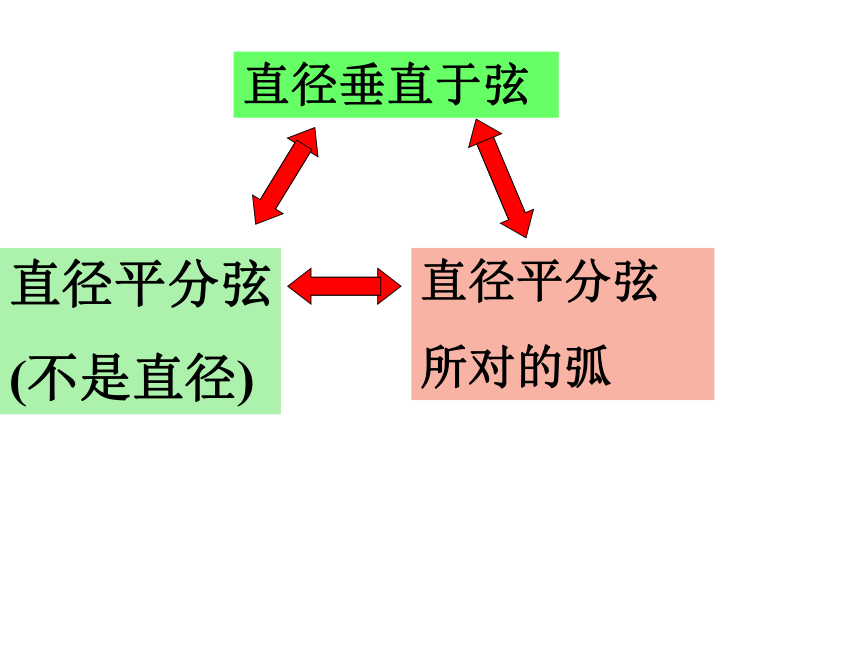
即:直径垂直于弦直径平分弦
(不是直径)直径平分弦
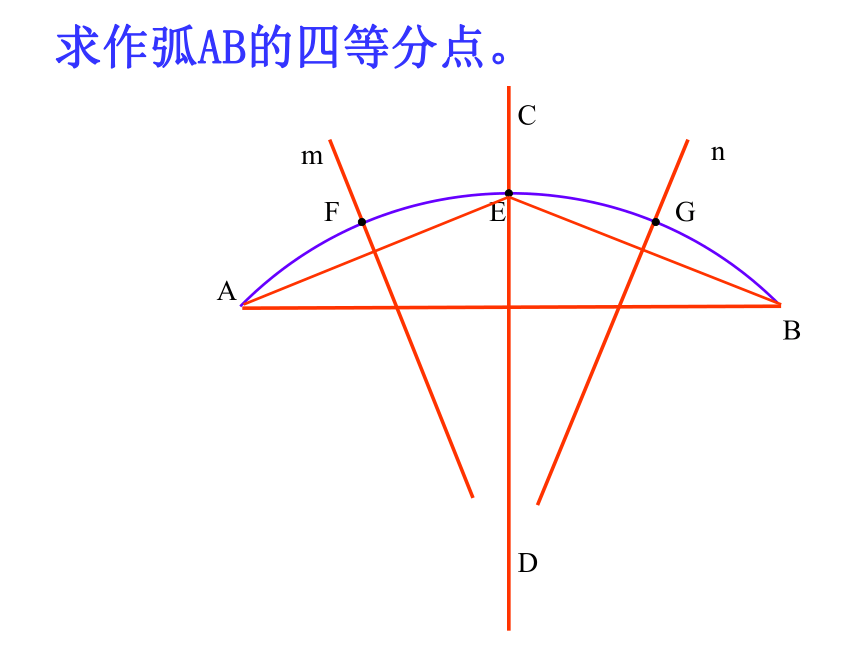
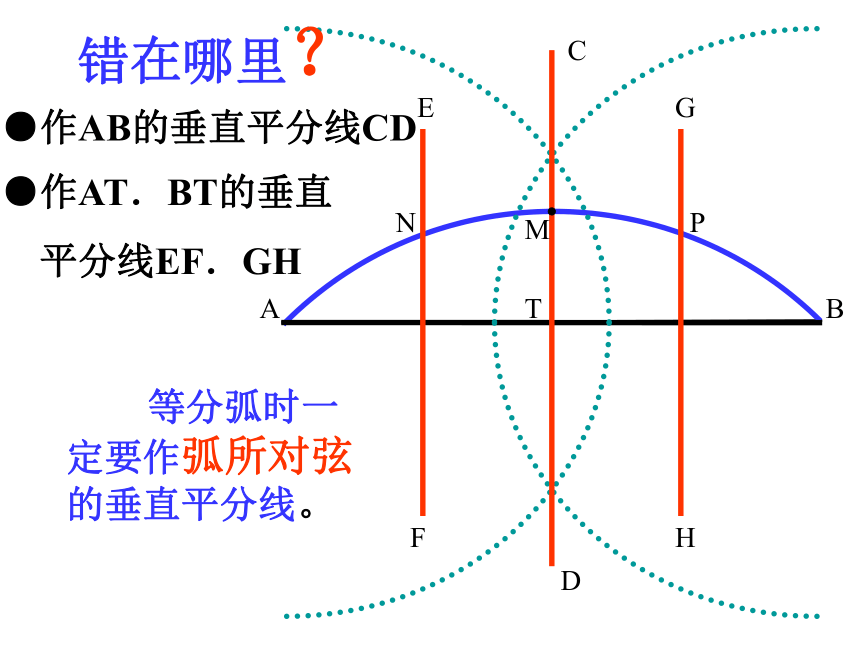
所对的弧CDABEFG 求作弧AB的四等分点。 mnCDABMTEFGHNP错在哪里?等分弧时一定要作弧所对弦的垂直平分线。●作AB的垂直平分线CD●作AT.BT的垂直
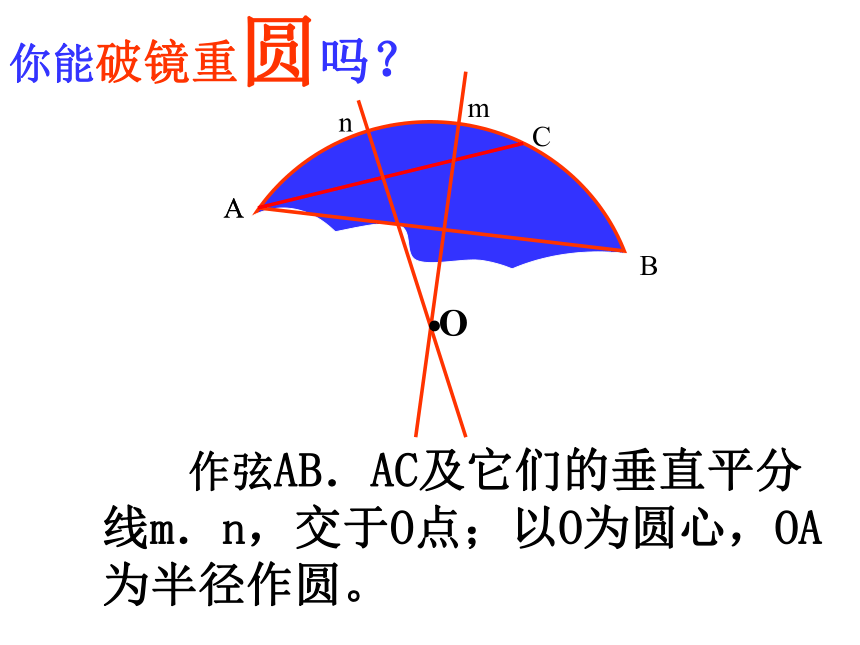
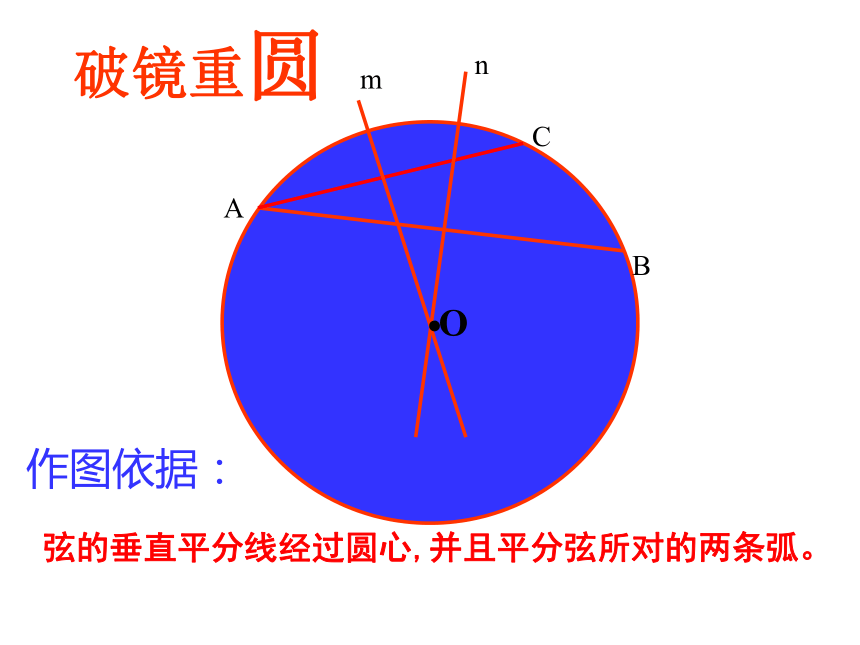
平分线EF.GH你能破镜重圆吗?ABACmn·O 作弦AB.AC及它们的垂直平分线m.n,交于O点;以O为圆心,OA为半径作圆。破镜重圆ABCmn·O 弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
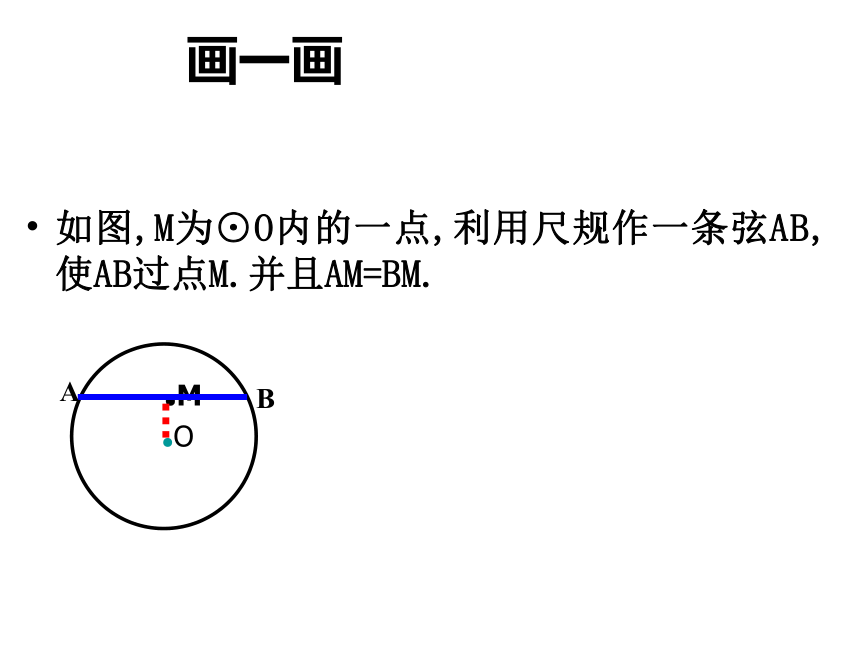
作图依据:画一画如图,M为⊙O内的一点,利用尺规作一条弦AB,使AB过点M.并且AM=BM.已知:AB是⊙O直径,OC⊥AD
求证:BD=2OC.AOBCD半径为5的圆中,有两条平行弦AB 和CD,并且AB =6,CD=8,求AB和CD间的距离.做这类问题是,思考问题一定要全面,考虑到多种情况。挑战自我如图,⊙O 与矩形 ABCD 交于 E , F ,G ,H , AH=4, HG=6,BE=2
求:EF。MN462E已知:AB是⊙O直径,CD
是弦,AE⊥CD,BF⊥CD
求证:EC=DFH已知:AB是⊙O直径,AB=10,弦CD=6,点A和点B到直线CD的距离之和等于______.AOBECDFH挑战自我对于一个圆中的弦长a、圆心到弦的距离d、圆半径r、弓形高h,这四个量中,只要已知其中任意两个量,就可以求出另外两个量,如图有:⑴d + h = r一条排水管的截面如图所示已知排水管的半径 OB=10 ,水面宽 AB=16 。求水深DC1088解:作 OC ⊥ AB 于 C,由垂径定理得:
AC=1/2 AB=0.5 × 16=8 由勾股定理得:CD=OD-OC=4
DC一条排水管的截面如图所示已知排水管的半径 OB=10 ,水面宽 AB=16 。求水深ABCP 如图,AB是⊙O的任意一条弦,OC⊥AB,垂足为P,若 CP=7cm,AB=28cm ,你能求出这面镜子的半径吗?O714综合应用垂径定理和勾股定理可求得半径如图为一圆弧形拱桥,半径OA = 10m,拱高为4m,求拱桥跨度AB的长。 赵州石拱桥1.1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(弧所对是弦的长)为 37.4 m,拱高(弧的中点到弦的距离,也叫弓形高)为7.2m,求桥拱的半径(精确到0.1m).你是第一个告诉同学们解题方法和结果的吗?例题赵州桥原名安济桥,俗称大石桥,建于隋炀帝大业年间(595-605年),至今已有1400年的历史,是今天世界上最古老的石拱桥。上面修成平坦的桥面,以行车走人.赵州桥的特点是“敞肩式”,是石拱桥结构中最先进的一种。其设计者是隋朝匠师李春。它的桥身弧线优美,远眺犹如苍龙飞驾,又似长虹饮涧。尤其是栏板以及望栓上的浮雕。充分显示整个大桥堪称一件精美的艺术珍品,称得上是隋唐时代石雕艺术的精品。1991年被列为世界文化遗产. 赵州石拱桥解:如图,用 表示桥拱, 所在圆的圆心为O,半径为Rm,
经过圆心O作弦AB的垂线OD,D为垂足,与 相交于点C.根
据垂径定理,D是AB的中点,C是 的中点,CD就是拱高.
由题设在Rt△OAD中,由勾股定理,得解得 R≈27.9(m).答:赵州石拱桥的桥拱半径约为27.9m.某一公路隧道的形状如图,半圆拱的圆心距离地面2m,半径为1.5m。一辆高3m,宽2.3m的集装箱卡车能顺利通过吗?再见
即:直径垂直于弦直径平分弦
(不是直径)直径平分弦
所对的弧CDABEFG 求作弧AB的四等分点。 mnCDABMTEFGHNP错在哪里?等分弧时一定要作弧所对弦的垂直平分线。●作AB的垂直平分线CD●作AT.BT的垂直
平分线EF.GH你能破镜重圆吗?ABACmn·O 作弦AB.AC及它们的垂直平分线m.n,交于O点;以O为圆心,OA为半径作圆。破镜重圆ABCmn·O 弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
作图依据:画一画如图,M为⊙O内的一点,利用尺规作一条弦AB,使AB过点M.并且AM=BM.已知:AB是⊙O直径,OC⊥AD
求证:BD=2OC.AOBCD半径为5的圆中,有两条平行弦AB 和CD,并且AB =6,CD=8,求AB和CD间的距离.做这类问题是,思考问题一定要全面,考虑到多种情况。挑战自我如图,⊙O 与矩形 ABCD 交于 E , F ,G ,H , AH=4, HG=6,BE=2
求:EF。MN462E已知:AB是⊙O直径,CD
是弦,AE⊥CD,BF⊥CD
求证:EC=DFH已知:AB是⊙O直径,AB=10,弦CD=6,点A和点B到直线CD的距离之和等于______.AOBECDFH挑战自我对于一个圆中的弦长a、圆心到弦的距离d、圆半径r、弓形高h,这四个量中,只要已知其中任意两个量,就可以求出另外两个量,如图有:⑴d + h = r一条排水管的截面如图所示已知排水管的半径 OB=10 ,水面宽 AB=16 。求水深DC1088解:作 OC ⊥ AB 于 C,由垂径定理得:
AC=1/2 AB=0.5 × 16=8 由勾股定理得:CD=OD-OC=4
DC一条排水管的截面如图所示已知排水管的半径 OB=10 ,水面宽 AB=16 。求水深ABCP 如图,AB是⊙O的任意一条弦,OC⊥AB,垂足为P,若 CP=7cm,AB=28cm ,你能求出这面镜子的半径吗?O714综合应用垂径定理和勾股定理可求得半径如图为一圆弧形拱桥,半径OA = 10m,拱高为4m,求拱桥跨度AB的长。 赵州石拱桥1.1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(弧所对是弦的长)为 37.4 m,拱高(弧的中点到弦的距离,也叫弓形高)为7.2m,求桥拱的半径(精确到0.1m).你是第一个告诉同学们解题方法和结果的吗?例题赵州桥原名安济桥,俗称大石桥,建于隋炀帝大业年间(595-605年),至今已有1400年的历史,是今天世界上最古老的石拱桥。上面修成平坦的桥面,以行车走人.赵州桥的特点是“敞肩式”,是石拱桥结构中最先进的一种。其设计者是隋朝匠师李春。它的桥身弧线优美,远眺犹如苍龙飞驾,又似长虹饮涧。尤其是栏板以及望栓上的浮雕。充分显示整个大桥堪称一件精美的艺术珍品,称得上是隋唐时代石雕艺术的精品。1991年被列为世界文化遗产. 赵州石拱桥解:如图,用 表示桥拱, 所在圆的圆心为O,半径为Rm,
经过圆心O作弦AB的垂线OD,D为垂足,与 相交于点C.根
据垂径定理,D是AB的中点,C是 的中点,CD就是拱高.
由题设在Rt△OAD中,由勾股定理,得解得 R≈27.9(m).答:赵州石拱桥的桥拱半径约为27.9m.某一公路隧道的形状如图,半圆拱的圆心距离地面2m,半径为1.5m。一辆高3m,宽2.3m的集装箱卡车能顺利通过吗?再见
同课章节目录
