青岛版数学九年级上册3.6 弧长及扇形面积的计算 课件(共16张PPT)
文档属性
| 名称 | 青岛版数学九年级上册3.6 弧长及扇形面积的计算 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 719.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-22 07:46:38 | ||
图片预览





文档简介
(共16张PPT)
3.6 弧长及扇形面积的计算
1、经历探索弧长计算公式及扇形面积计算公式的过程。
2、了解弧长计算公式及扇形面积的计算公式,并会应用公式解决问题.
重点:掌握弧长及扇形面积计算公式。并会应用公式解决问题.
学习目标
情景导入
问题1 如图,在运动会的4×100米比赛中,甲和乙分别在第1跑道和第2跑道,为什么他们的起跑线不在同一处?
因为要保证这些弯道的“展直长度”是一样的.
问题2 怎样来计算弯道的“展直长度”?
获取新知
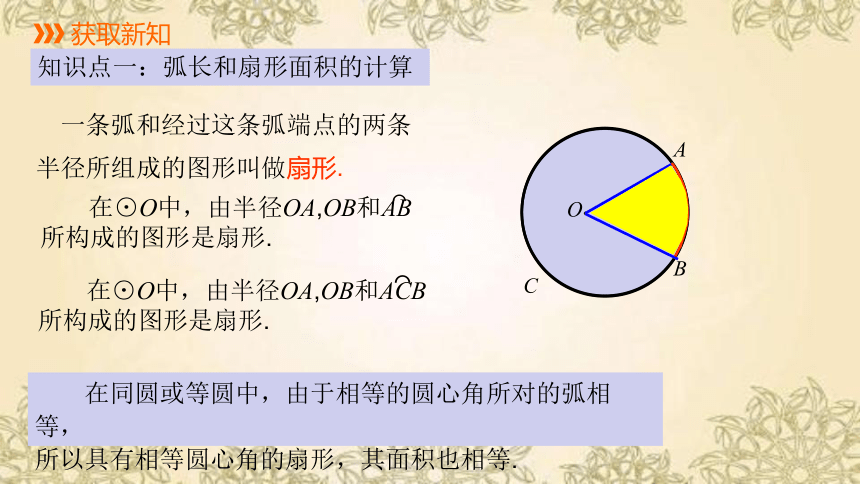
知识点一:弧长和扇形面积的计算
一条弧和经过这条弧端点的两条
半径所组成的图形叫做扇形.
A
B
O
C
在同圆或等圆中,由于相等的圆心角所对的弧相等,
所以具有相等圆心角的扇形,其面积也相等.
在⊙O中,由半径OA,OB和AB
所构成的图形是扇形.
⌒
在⊙O中,由半径OA,OB和ACB
所构成的图形是扇形.
⌒
弧是圆的一部分,弧长就是圆周长的一部分.在半径为R的圆中, 360 的圆心角所对的弧长就是____________.
圆周长
(1)1 的圆心角所对的弧长 l 是:
(2)n 的圆心角所对的弧长 l 是:
扇形是圆周的一部分,扇形面积就是圆面积的一部分.在半径为R的圆中, 360 的圆心角所对的扇形的面积就是____________.
圆面积
(1)1 的圆心角所对的扇形面积 S 是:
(2)n 的圆心角所对的弧长S 是:
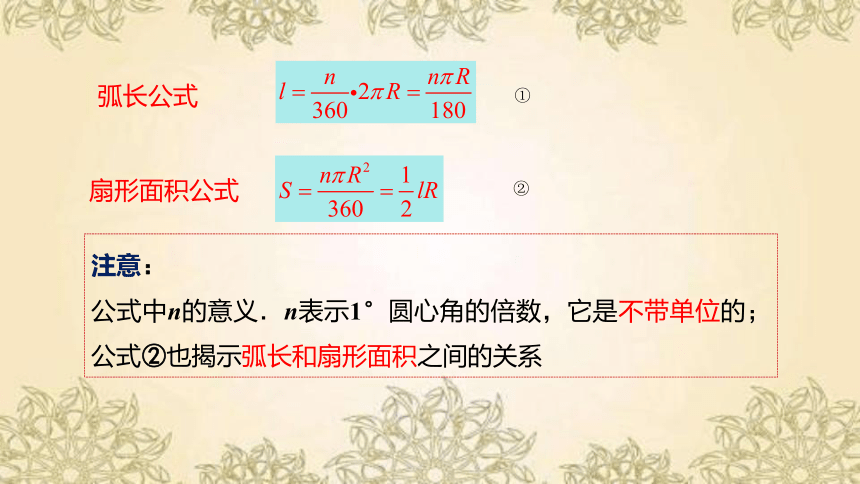
弧长公式
扇形面积公式
①
②
注意:
公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;公式②也揭示弧长和扇形面积之间的关系
探索新知
如图,一条公路的转弯处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600米,E为弧CD上一点,且OE⊥CD,垂足为F,
OF=300 米,则这段弯路的长度为( )
A.200π米 B.100π米
C.400π米 D.300π米
例1
A
导引:设这段弯路的半径为R米.∵OE⊥CD,∴CF= CD= ×600=300(米).
根据勾股定理,得OC2=CF2+OF2,即R2=3002+(300 )2 .
解得R=600 . ∴∠COF=30°. ∴∠COD=60°.
∴这段弯路的长度为 =200π(米) .
探索新知
总 结
求弧长需要两个条件:
(1)弧所在圆的半径;
(2)弧所对的圆心角.当题中没有直接给出这两个条件时,则需利用圆的相关知识:弦、弦心距、圆周角等求出圆的半径或弧所对的圆心角.
探索新知
例2 如图,⊙O的半径为10 cm .
(1)如果∠AOB=100°,求 的长及扇形AOB的面积 . (结果保留一位小数)
(2)已知 =25 cm,求∠BOC的度数 . (结果精确到1°)
探索新知
解:(1) r=10 cm,∠AOB=100°,由弧长和扇形面积公式,得
所以 的长约为17. 4 cm,扇形AOB的面积约为87. 2 cm2 .
(2)r=10 cm, =25 cm,由弧长公式,得
所以∠BOC约为143° .
探索新知
扇形的面积公式有两个,若已知圆心角的度数和
半径,则用S扇形= ;若已知扇形的弧长和半径,
则用S扇形= lR(l是扇形的弧长).
总 结
随堂训练
1.如图,⊙O是△ABC的外接圆,BC=2,∠BAC=30°,则劣弧BC的长等于( )
2.如图,分别以n边形的顶点为圆心,以1cm为半径画圆,当n=2019时,则图中阴影部分的面积之和为( )
A.2πcm2 B.πcm2
C.2018πcm2 D.2019πcm2
C
B
3.如图,在扇形AOB中,AC为弦,∠AOB=130°,∠CAO=60°,OA=6,则 BC 的长为 .
(
4.(1)已知半径为2的扇形,面积为π,则它的圆心角的度数= .
(2)已知半径为2 cm的扇形,其弧长为π,则这个扇形的面积S扇= .
(3)已知半径为2的扇形,面积为π,则这个扇形的弧长= .
(4)已知扇形的半径为5 cm,面积为20 cm2,则扇形弧长为 cm.
(5)已知扇形的圆心角为210°,弧长是28π,则扇形的面积为 .
120°
8
谢谢聆听
3.6 弧长及扇形面积的计算
1、经历探索弧长计算公式及扇形面积计算公式的过程。
2、了解弧长计算公式及扇形面积的计算公式,并会应用公式解决问题.
重点:掌握弧长及扇形面积计算公式。并会应用公式解决问题.
学习目标
情景导入
问题1 如图,在运动会的4×100米比赛中,甲和乙分别在第1跑道和第2跑道,为什么他们的起跑线不在同一处?
因为要保证这些弯道的“展直长度”是一样的.
问题2 怎样来计算弯道的“展直长度”?
获取新知
知识点一:弧长和扇形面积的计算
一条弧和经过这条弧端点的两条
半径所组成的图形叫做扇形.
A
B
O
C
在同圆或等圆中,由于相等的圆心角所对的弧相等,
所以具有相等圆心角的扇形,其面积也相等.
在⊙O中,由半径OA,OB和AB
所构成的图形是扇形.
⌒
在⊙O中,由半径OA,OB和ACB
所构成的图形是扇形.
⌒
弧是圆的一部分,弧长就是圆周长的一部分.在半径为R的圆中, 360 的圆心角所对的弧长就是____________.
圆周长
(1)1 的圆心角所对的弧长 l 是:
(2)n 的圆心角所对的弧长 l 是:
扇形是圆周的一部分,扇形面积就是圆面积的一部分.在半径为R的圆中, 360 的圆心角所对的扇形的面积就是____________.
圆面积
(1)1 的圆心角所对的扇形面积 S 是:
(2)n 的圆心角所对的弧长S 是:
弧长公式
扇形面积公式
①
②
注意:
公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;公式②也揭示弧长和扇形面积之间的关系
探索新知
如图,一条公路的转弯处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600米,E为弧CD上一点,且OE⊥CD,垂足为F,
OF=300 米,则这段弯路的长度为( )
A.200π米 B.100π米
C.400π米 D.300π米
例1
A
导引:设这段弯路的半径为R米.∵OE⊥CD,∴CF= CD= ×600=300(米).
根据勾股定理,得OC2=CF2+OF2,即R2=3002+(300 )2 .
解得R=600 . ∴∠COF=30°. ∴∠COD=60°.
∴这段弯路的长度为 =200π(米) .
探索新知
总 结
求弧长需要两个条件:
(1)弧所在圆的半径;
(2)弧所对的圆心角.当题中没有直接给出这两个条件时,则需利用圆的相关知识:弦、弦心距、圆周角等求出圆的半径或弧所对的圆心角.
探索新知
例2 如图,⊙O的半径为10 cm .
(1)如果∠AOB=100°,求 的长及扇形AOB的面积 . (结果保留一位小数)
(2)已知 =25 cm,求∠BOC的度数 . (结果精确到1°)
探索新知
解:(1) r=10 cm,∠AOB=100°,由弧长和扇形面积公式,得
所以 的长约为17. 4 cm,扇形AOB的面积约为87. 2 cm2 .
(2)r=10 cm, =25 cm,由弧长公式,得
所以∠BOC约为143° .
探索新知
扇形的面积公式有两个,若已知圆心角的度数和
半径,则用S扇形= ;若已知扇形的弧长和半径,
则用S扇形= lR(l是扇形的弧长).
总 结
随堂训练
1.如图,⊙O是△ABC的外接圆,BC=2,∠BAC=30°,则劣弧BC的长等于( )
2.如图,分别以n边形的顶点为圆心,以1cm为半径画圆,当n=2019时,则图中阴影部分的面积之和为( )
A.2πcm2 B.πcm2
C.2018πcm2 D.2019πcm2
C
B
3.如图,在扇形AOB中,AC为弦,∠AOB=130°,∠CAO=60°,OA=6,则 BC 的长为 .
(
4.(1)已知半径为2的扇形,面积为π,则它的圆心角的度数= .
(2)已知半径为2 cm的扇形,其弧长为π,则这个扇形的面积S扇= .
(3)已知半径为2的扇形,面积为π,则这个扇形的弧长= .
(4)已知扇形的半径为5 cm,面积为20 cm2,则扇形弧长为 cm.
(5)已知扇形的圆心角为210°,弧长是28π,则扇形的面积为 .
120°
8
谢谢聆听
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
