人教A版必修二6.3.2平面向量的正交分解及坐标运算 课堂、课后练习题(含解析)
文档属性
| 名称 | 人教A版必修二6.3.2平面向量的正交分解及坐标运算 课堂、课后练习题(含解析) | 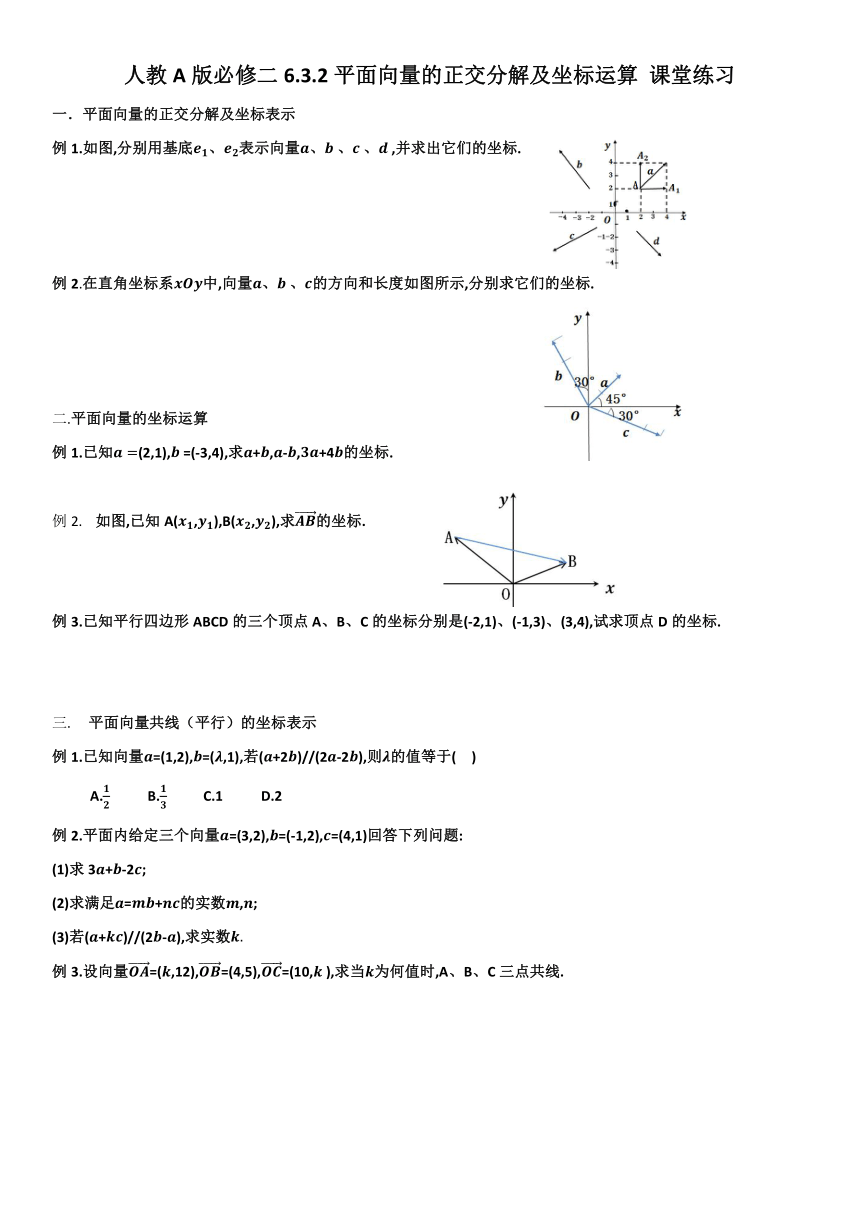 | |
| 格式 | docx | ||
| 文件大小 | 73.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-21 15:54:19 | ||
图片预览


文档简介
人教A版必修二6.3.2平面向量的正交分解及坐标运算 课堂练习
一.平面向量的正交分解及坐标表示
例1.如图,分别用基底、表示向量、、、,并求出它们的坐标.
例2.在直角坐标系中,向量、、的方向和长度如图所示,分别求它们的坐标.
二.平面向量的坐标运算
例1.已知(2,1),=(-3,4),求+,-,+4的坐标.
例2. 如图,已知A(,),B(,),求的坐标.
例3.已知平行四边形ABCD的三个顶点A、B、C的坐标分别是(-2,1)、(-1,3)、(3,4),试求顶点D的坐标.
三. 平面向量共线(平行)的坐标表示
例1.已知向量=(1,2),=(,1),若(+2)//(2-2),则的值等于( )
A. B. C.1 D.2
例2.平面内给定三个向量=(3,2),=(-1,2),=(4,1)回答下列问题:
(1)求3+-2;
(2)求满足=+的实数,;
(3)若(+)//(2-),求实数
例3.设向量=(,12),=(4,5),=(10,),求当为何值时,A、B、C三点共线.
答案:
一.平面向量的正交分解及坐标表示
例1. =2+3=(2,3) =2+3=(-2,3) =-2-3=(-2,-3) =2-3=(2,-3)
例2.=,=,=
二.平面向量的坐标运算
例1. +=(-1,5) -=(5,-3) +4=(-6,19).
例2. =- =(-,-).
例3. D的坐标为(2,2).
三. 平面向量共线(平行)的坐标表示
例1.答案:A
例2. (1) 3+-2 (2) (3)
例3.
人教A版必修二6.3.2平面向量的正交分解及坐标运算 课后练习
基础达标
1.设i,j是平面直角坐标系内分别与x轴,y轴正方向相同的两个单位向量,O为坐标原点,若=4i+2j,
=3i+4j,则2+的坐标是( )
A.(1,-2) B.(7,6) C.(5,0) D.(11,8)
2.设向量a=(1,2),b=(-3,5),c=(4,x),若a+b=λc(λ∈R),则λ+x的值为( )
A.- B. C.- D.
3.已知=(-2,4),=(2,6),则等于( )
A.(0,5) B.(0,1) C.(2,5) D.(2,1)
4.已知四边形ABCD的三个顶点A(0,2),B(-1,-2),C(3,1),且=2,则顶点D的坐标为( )
A. B. C.(3,2) D.(1,3)
5.已知A(-3,0),B(0,2),O为坐标原点,点C在∠AOB内,且∠AOC=45°,设=λ+(1-λ)(λ∈R),则λ的值为( )
A. B. C. D.
6.已知点A(-1,-5)和向量a=(2,3),若=3a,则点B的坐标为________.
7.已知向量a=(1,2),b=(-2,3),c=(4,1),若用a和b表示c,则c=________.
8.已知A(-1,2),B(2,8).若=,=-,则的坐标为________.
9.已知A(-2,4),B(3,-1),C(-3,-4).设=a,=b,=c.
(1)求3a+b-3c;
(2)求满足a=mb+nc的实数m,n的值.
10.已知向量=(4,3),=(-3,-1),点A(-1,-2).
(1)求线段BD的中点M的坐标;
(2)若点P(2,y)满足=λ(λ∈R),求λ与y的值.
能力提升
11.在△ABC中,点P在BC上,且=2,点Q是AC的中点,若=(4,3),=(1,5),则=________.
12.已知A(-3,0),B(0,2),O为坐标原点,点C在∠AOB内,|OC|=2,且∠AOC=,设=λ+(λ∈R),则λ=______.
答案:
1.选D. 解析:因为=(4,2),=(3,4),
所以2+=(8,4)+(3,4)=(11,8).
2. 选C.解析:由已知,可得(1,2)+(-3,5)=λ(4,x),所以解得所以λ+x=-,故选C.
3. 选D.解析:=(-)=(2,6)-(-2,4)=(2,1).
4.解析:选A.设点D(m,n),则由题意得(4,3)=2(m,n-2)=(2m,2n-4),故
解得即点D的坐标为,故选A.
5.解析: 选C.如图所示,因为∠AOC=45°,所以设C(x,-x),则=(x,-x).
又因为A(-3,0),B(0,2),
所以λ+(1-λ)=(-3λ,2-2λ),
所以 λ=.
6. 答案:(5,4)
解析:设O为坐标原点,因为=(-1,-5),=3a=(6,9),故=+=(5,4),故点B的坐标为(5,4).
7. 答案:2a-b
解析:设c=xa+yb,则(x,2x)+(-2y,3y)=(x-2y,2x+3y)=(4,1).故解得
所以c=2a-b.
8. 答案:(1,2)
解析:==(3,6)=(1,2),=-=-(3,6)=(-2,-4),=+=(-1,-2),
所以=(1,2).
9.解:由已知得a=(5,-5),b=(-6,-3),c=(1,8).
(1)3a+b-3c=3(5,-5)+(-6,-3)-3(1,8)=(15-6-3,-15-3-24)=(6,-42).
(2)因为mb+nc=(-6m+n,-3m+8n),
所以解得
10.解:(1)设B(x1,y1),
因为=(4,3),A(-1,-2),所以(x1+1,y1+2)=(4,3),所以所以所以B(3,1).
同理可得D(-4,-3),
设BD的中点M(x2,y2),则x2==-,y2==-1.所以M.
(2)由=(3,1)-(2,y)=(1,1-y),=(-4,-3)-(3,1)=(-7,-4),
又=λ(λ∈R),
所以(1,1-y)=λ(-7,-4)=(-7λ,-4λ),所以
所以
11.解析:-==(1,5)-(4,3)=(-3,2),因为点Q是AC的中点,所以=,
所以=+=(1,5)+(-3,2)=(-2,7).因为=2,所以=+=3=3(-2,7)=(-6,21).
答案:(-6,21)
12.解析:过C作CE⊥x轴于点E,由∠AOC=知,|OE|=|CE|=2,所以=+=λ+,即=λ,所以(-2,0)=λ(-3,0),故λ=.
答案:
一.平面向量的正交分解及坐标表示
例1.如图,分别用基底、表示向量、、、,并求出它们的坐标.
例2.在直角坐标系中,向量、、的方向和长度如图所示,分别求它们的坐标.
二.平面向量的坐标运算
例1.已知(2,1),=(-3,4),求+,-,+4的坐标.
例2. 如图,已知A(,),B(,),求的坐标.
例3.已知平行四边形ABCD的三个顶点A、B、C的坐标分别是(-2,1)、(-1,3)、(3,4),试求顶点D的坐标.
三. 平面向量共线(平行)的坐标表示
例1.已知向量=(1,2),=(,1),若(+2)//(2-2),则的值等于( )
A. B. C.1 D.2
例2.平面内给定三个向量=(3,2),=(-1,2),=(4,1)回答下列问题:
(1)求3+-2;
(2)求满足=+的实数,;
(3)若(+)//(2-),求实数
例3.设向量=(,12),=(4,5),=(10,),求当为何值时,A、B、C三点共线.
答案:
一.平面向量的正交分解及坐标表示
例1. =2+3=(2,3) =2+3=(-2,3) =-2-3=(-2,-3) =2-3=(2,-3)
例2.=,=,=
二.平面向量的坐标运算
例1. +=(-1,5) -=(5,-3) +4=(-6,19).
例2. =- =(-,-).
例3. D的坐标为(2,2).
三. 平面向量共线(平行)的坐标表示
例1.答案:A
例2. (1) 3+-2 (2) (3)
例3.
人教A版必修二6.3.2平面向量的正交分解及坐标运算 课后练习
基础达标
1.设i,j是平面直角坐标系内分别与x轴,y轴正方向相同的两个单位向量,O为坐标原点,若=4i+2j,
=3i+4j,则2+的坐标是( )
A.(1,-2) B.(7,6) C.(5,0) D.(11,8)
2.设向量a=(1,2),b=(-3,5),c=(4,x),若a+b=λc(λ∈R),则λ+x的值为( )
A.- B. C.- D.
3.已知=(-2,4),=(2,6),则等于( )
A.(0,5) B.(0,1) C.(2,5) D.(2,1)
4.已知四边形ABCD的三个顶点A(0,2),B(-1,-2),C(3,1),且=2,则顶点D的坐标为( )
A. B. C.(3,2) D.(1,3)
5.已知A(-3,0),B(0,2),O为坐标原点,点C在∠AOB内,且∠AOC=45°,设=λ+(1-λ)(λ∈R),则λ的值为( )
A. B. C. D.
6.已知点A(-1,-5)和向量a=(2,3),若=3a,则点B的坐标为________.
7.已知向量a=(1,2),b=(-2,3),c=(4,1),若用a和b表示c,则c=________.
8.已知A(-1,2),B(2,8).若=,=-,则的坐标为________.
9.已知A(-2,4),B(3,-1),C(-3,-4).设=a,=b,=c.
(1)求3a+b-3c;
(2)求满足a=mb+nc的实数m,n的值.
10.已知向量=(4,3),=(-3,-1),点A(-1,-2).
(1)求线段BD的中点M的坐标;
(2)若点P(2,y)满足=λ(λ∈R),求λ与y的值.
能力提升
11.在△ABC中,点P在BC上,且=2,点Q是AC的中点,若=(4,3),=(1,5),则=________.
12.已知A(-3,0),B(0,2),O为坐标原点,点C在∠AOB内,|OC|=2,且∠AOC=,设=λ+(λ∈R),则λ=______.
答案:
1.选D. 解析:因为=(4,2),=(3,4),
所以2+=(8,4)+(3,4)=(11,8).
2. 选C.解析:由已知,可得(1,2)+(-3,5)=λ(4,x),所以解得所以λ+x=-,故选C.
3. 选D.解析:=(-)=(2,6)-(-2,4)=(2,1).
4.解析:选A.设点D(m,n),则由题意得(4,3)=2(m,n-2)=(2m,2n-4),故
解得即点D的坐标为,故选A.
5.解析: 选C.如图所示,因为∠AOC=45°,所以设C(x,-x),则=(x,-x).
又因为A(-3,0),B(0,2),
所以λ+(1-λ)=(-3λ,2-2λ),
所以 λ=.
6. 答案:(5,4)
解析:设O为坐标原点,因为=(-1,-5),=3a=(6,9),故=+=(5,4),故点B的坐标为(5,4).
7. 答案:2a-b
解析:设c=xa+yb,则(x,2x)+(-2y,3y)=(x-2y,2x+3y)=(4,1).故解得
所以c=2a-b.
8. 答案:(1,2)
解析:==(3,6)=(1,2),=-=-(3,6)=(-2,-4),=+=(-1,-2),
所以=(1,2).
9.解:由已知得a=(5,-5),b=(-6,-3),c=(1,8).
(1)3a+b-3c=3(5,-5)+(-6,-3)-3(1,8)=(15-6-3,-15-3-24)=(6,-42).
(2)因为mb+nc=(-6m+n,-3m+8n),
所以解得
10.解:(1)设B(x1,y1),
因为=(4,3),A(-1,-2),所以(x1+1,y1+2)=(4,3),所以所以所以B(3,1).
同理可得D(-4,-3),
设BD的中点M(x2,y2),则x2==-,y2==-1.所以M.
(2)由=(3,1)-(2,y)=(1,1-y),=(-4,-3)-(3,1)=(-7,-4),
又=λ(λ∈R),
所以(1,1-y)=λ(-7,-4)=(-7λ,-4λ),所以
所以
11.解析:-==(1,5)-(4,3)=(-3,2),因为点Q是AC的中点,所以=,
所以=+=(1,5)+(-3,2)=(-2,7).因为=2,所以=+=3=3(-2,7)=(-6,21).
答案:(-6,21)
12.解析:过C作CE⊥x轴于点E,由∠AOC=知,|OE|=|CE|=2,所以=+=λ+,即=λ,所以(-2,0)=λ(-3,0),故λ=.
答案:
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
