数学人教A版(2019)选择性必修第一册1.4.1用空间向量研究直线、平面的位置关系(共29张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册1.4.1用空间向量研究直线、平面的位置关系(共29张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-21 15:54:57 | ||
图片预览



文档简介
(共29张PPT)
1.4.1用空间向量研究
直线、平面的位置关系
复习导入
新知探究
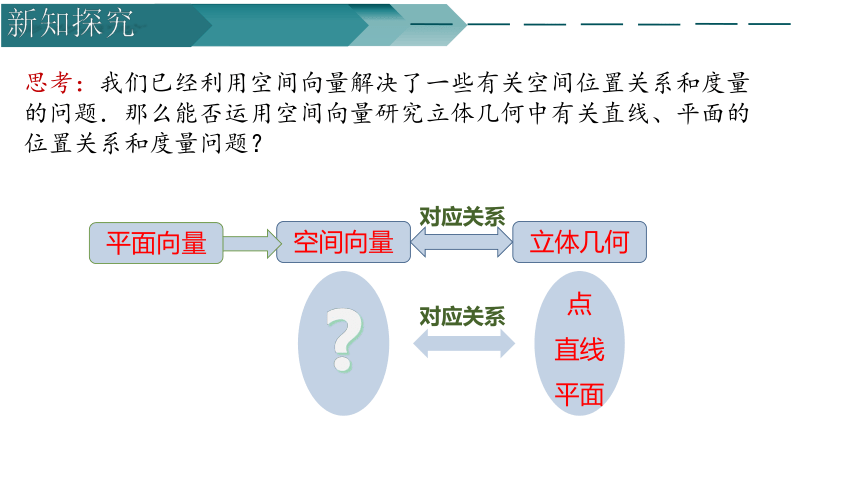
思考:我们已经利用空间向量解决了一些有关空间位置关系和度量的问题.那么能否运用空间向量研究立体几何中有关直线、平面的位置关系和度量问题?
对应关系
点
直线
平面
对应关系
空间向量
立体几何
平面向量
新知探究
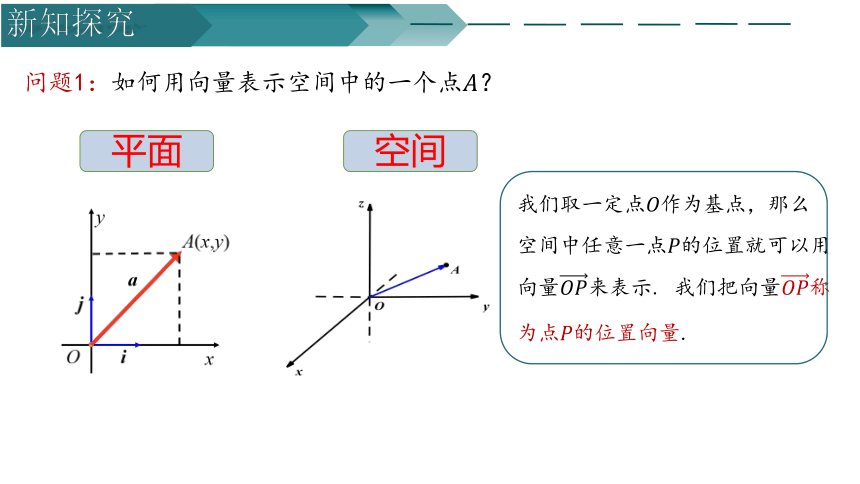
问题1:如何用向量表示空间中的一个点?
平面
空间
我们取一定点作为基点,那么空间中任意一点的位置就可以用向量来表示. 我们把向量称为点的位置向量.
新知探究
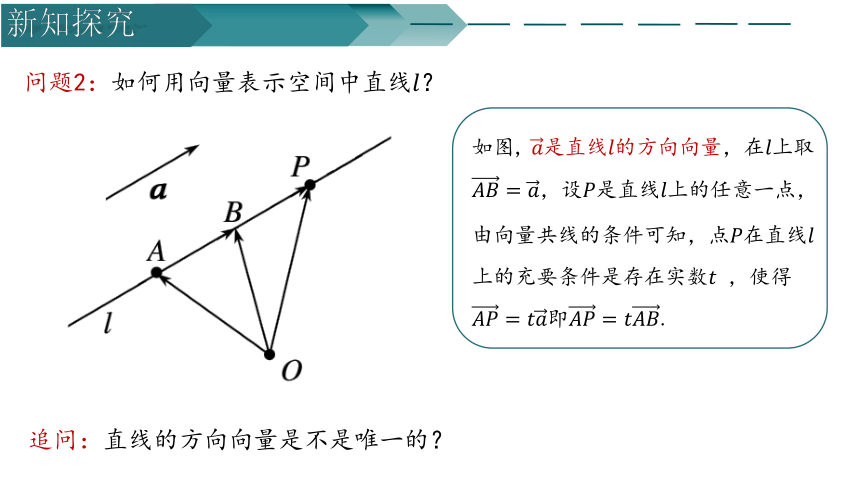
问题2:如何用向量表示空间中直线?
如图, 是直线的方向向量,在上取,设是直线上的任意一点,由向量共线的条件可知,点在直线上的充要条件是存在实数 ,使得即.
追问:直线的方向向量是不是唯一的?
新知探究
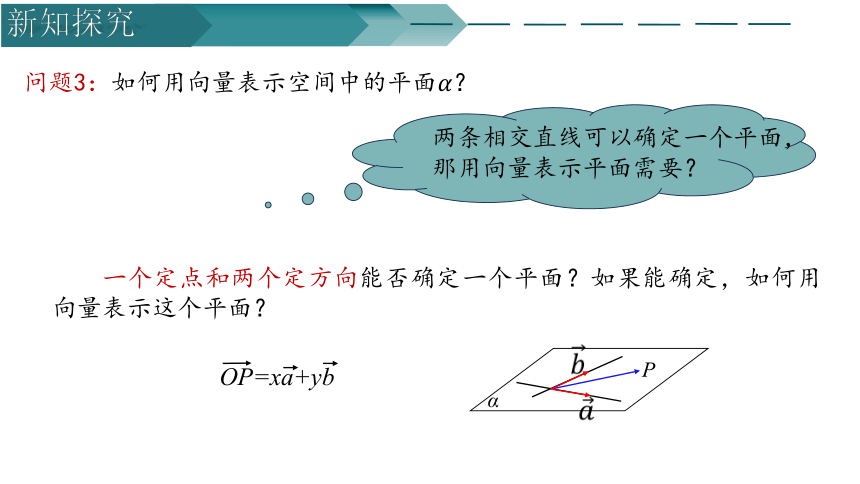
问题3:如何用向量表示空间中的平面?
两条相交直线可以确定一个平面,那用向量表示平面需要?
一个定点和两个定方向能否确定一个平面?如果能确定,如何用向量表示这个平面?
α
OP=xa+yb
P
新知探究
问题3:如何用向量表示空间中的平面?
α
OP=xa+yb
P
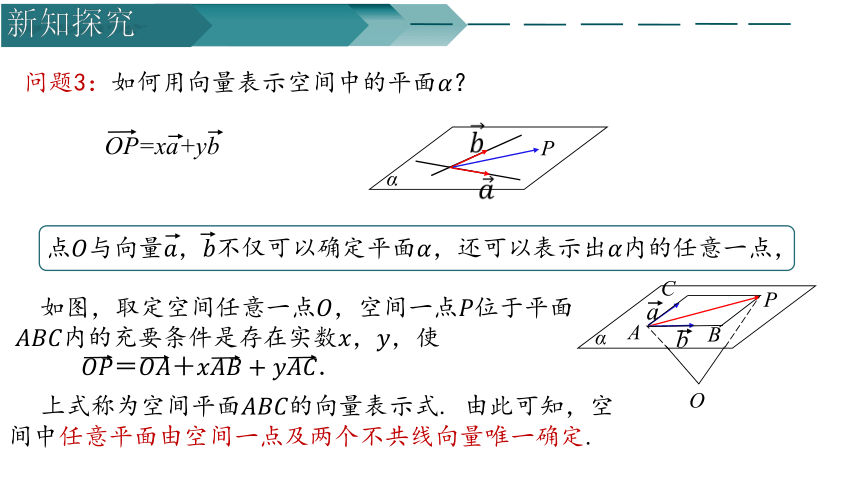
如图,取定空间任意一点,空间一点位于平面内的充要条件是存在实数,,使
B
α
A
C
P
O
a
b
上式称为空间平面的向量表示式. 由此可知,空间中任意平面由空间一点及两个不共线向量唯一确定.
点与向量,不仅可以确定平面,还可以表示出内的任意一点,
新知探究
追问:能否用一个向量表示空间中的平面?
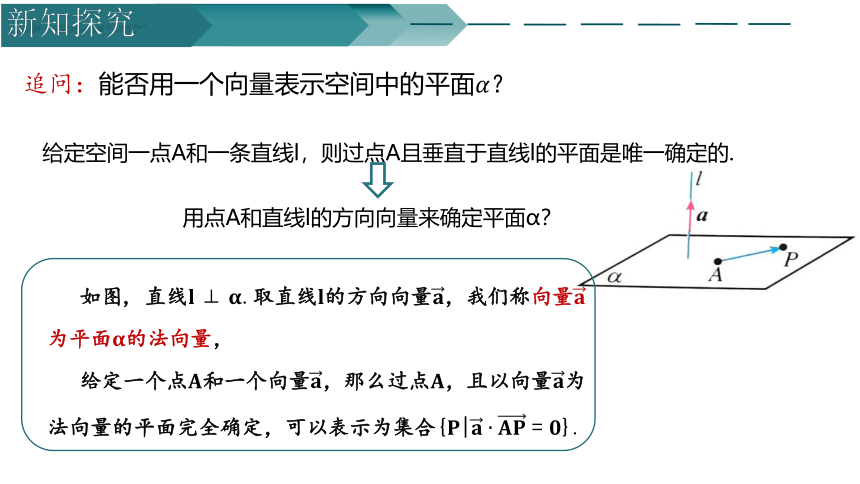
给定空间一点和一条直线,则过点且垂直于直线的平面是唯一确定的.
用点和直线的方向向量来确定平面?
如图, 直线取直线的方向向量,我们称向量为平面的法向量,
给定一个点和一个向量,那么过点,且以向量为法向量的平面完全确定,可以表示为集合
例题讲解
练习1.
1、判断正误.(正确的画“√”,错误的画“×”)
(1)直线的方向向量是唯一的. ( )
(2)若点,是平面上的任意两点,是平面的法向量,则 .( )
(3)由空间点和直线的方向向量能表示直线上的任意一点. ( )
(4)空间中任意平面由空间一点及两个不共线向量唯一确定. ( )
2、若(2,1,1),(1,2,2)在直线上,则直线的一个方向向量为( )
(2,1,1) (-2,2,2) (-3,2,1) (2,1,-1)
答案:1、(1)× (2)√ (3)√ (4)√
答案:2、
例题讲解
例1.如图,在长方体中,是的中点.以为原点,所在直线分别为轴、轴、轴,建立如图所示的空间直角坐标系.
(1)求平面的法向量;(2)求平面的法向量.
解:(1)因为轴垂直于平面,
所以是平面的一个法向量.
例题讲解
例1.如图,在长方体中,
是的中点.以为原点,所在直线分别为轴、轴、轴,
建立如图所示的空间直角坐标系.(2)求平面的法向量.
解:(2)因为是的中点,所以,的坐标分别为,,.
因此,.
设是平面的法向量,则,
所以所以
取,则,.于是是平面的一个法向量.
利用待定系数法求法向量的步骤
设向量
设平面法向量n=(x,y,z)
列方程组
选向量
在平面内选取两个不共线向量AB,AC
取x,y,z中一个为非零值(常取±1)
赋值
结论
得到平面的一个法向量
n·AB=0
n·AC=0
列出等式
例题讲解
练习2. 已知(0,1,1),(-1,1,1),(1,0,0),则平面的一个 法向量为 ( )
.(0,1,-1) .(-1,0,1) .(1,1,1) .(-1,0,0)
解:设平面的法向量为,由,,可得
取,得, -1
选
新知探究
思考:既然点线面均可用向量表示,那是否可以利用向量进一步研究点线面间的位置关系呢?
问题4:由直线与直线的平行关系,可以得到这两条直线的方向向量有什么关系呢?
所以,
使得
新知探究
问题5:由直线与平面的平行关系,可以得到直线的方向向量与平面的法向量有什么关系呢?
新知探究
问题6:由平面与平面的平行关系,可以得到着两个平面的法向量有什么关系呢?
使得
新知探究
线面的位置关系 向量的位置关系 向量的运算 向量运算的坐标表示
∥
∥ β
使得
使得
= =
+
= =
例题讲解
例2.证明“平面与平面平行的判定定理”:若一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.
已知:如图,,,,,.
求证:
证明:如图,取平面的法向量,直线的方向向量,.
因为,,所以.
因为
所以对任意点,存在,使得.
从而.
所以,向量也是平面的法向量.故
例题讲解
例3.如图,在长方体中,.线段上是否存在点,使得平面?
解:以为原点,,,所在直线分别为轴、轴、轴,建立如图所示的空间直角坐标系.因为,,的坐标分别为,,,
所以,.
设是平面的法向量,则,,即所以
例题讲解
例3.如图,在长方体中,.线段上是否存在点,使得平面?
取,则,.
所以,是平面的一个法向量.
由,,的坐标分别为,,,得
,.
设点满足则,
所以.
令,得,解得,
此时平面,这样的点存在.
所以,当,即为的中点时,平面.
例题讲解
练习3.如图,已知正方体的棱长为2,分别是,的中点,求证:平面.
证明:建立如图所示空间直角坐标系,
则有
所以,,.
设是平面的法向量,则,,
即得令,则,
所以.因为,所以.
又因为平面,所以平面.
例题讲解
练习4.已知正方体的棱长为2,分别是,的中点,求证:平面平面.
证明:建立如图所示空间直角坐标系,则有
所以,
设是平面的法向量,则,,
即得
令,则,所以.
又平面的法向量 .
,所以平面平面.
新知探究
问题7:直线、平面间的垂直关系又如何用向量表示呢?
线线垂直
线面垂直
面面垂直
,使得
例题讲解
例4.如图,在平行六面体中,求证:直线平面.
证明:设,,,则为空间的一个基底,
且,,.
因为
所以
在平面上,取,为基向量,则对于平面上任意一点,
存在唯一的有序实数对,使得
所以,
所以是平面的法向量.所以平面.
例题讲解
例5. 证明“平面与平面垂直的判定定理”:若一个平面过另一个平面的垂线,则这两个平面垂直.
已知:如图,,求证:.
证明:取直线的方向向量,平面的法向量.
因为,所以是平面的法向量.
因为,而是平面的法向量,所以.
所以.
例题讲解
练习5.在四棱锥 中,底面 是正方形, ⊥底面 ,且 = ,
是 的中点.求证:平面 ⊥平面 .
证明:设,建立如图所示的空间直角坐标系,
设平面的法向量为
易知
∴即
令,可得平面的一个法向量为.
∵平面,∴平面的一个法向量为
∵,∴平平面.
小结
用空间向量研究直线、平面的位置关系
线面位置关系的向量表示
点线面的向量表示
点
线
面
OP=xa+yb
平面的法向量:
小结
线线平行
线面平行
面面平行
使得
使得
小结
线线垂直
线面垂直
面面垂直
,使得
1.4.1用空间向量研究
直线、平面的位置关系
复习导入
新知探究
思考:我们已经利用空间向量解决了一些有关空间位置关系和度量的问题.那么能否运用空间向量研究立体几何中有关直线、平面的位置关系和度量问题?
对应关系
点
直线
平面
对应关系
空间向量
立体几何
平面向量
新知探究
问题1:如何用向量表示空间中的一个点?
平面
空间
我们取一定点作为基点,那么空间中任意一点的位置就可以用向量来表示. 我们把向量称为点的位置向量.
新知探究
问题2:如何用向量表示空间中直线?
如图, 是直线的方向向量,在上取,设是直线上的任意一点,由向量共线的条件可知,点在直线上的充要条件是存在实数 ,使得即.
追问:直线的方向向量是不是唯一的?
新知探究
问题3:如何用向量表示空间中的平面?
两条相交直线可以确定一个平面,那用向量表示平面需要?
一个定点和两个定方向能否确定一个平面?如果能确定,如何用向量表示这个平面?
α
OP=xa+yb
P
新知探究
问题3:如何用向量表示空间中的平面?
α
OP=xa+yb
P
如图,取定空间任意一点,空间一点位于平面内的充要条件是存在实数,,使
B
α
A
C
P
O
a
b
上式称为空间平面的向量表示式. 由此可知,空间中任意平面由空间一点及两个不共线向量唯一确定.
点与向量,不仅可以确定平面,还可以表示出内的任意一点,
新知探究
追问:能否用一个向量表示空间中的平面?
给定空间一点和一条直线,则过点且垂直于直线的平面是唯一确定的.
用点和直线的方向向量来确定平面?
如图, 直线取直线的方向向量,我们称向量为平面的法向量,
给定一个点和一个向量,那么过点,且以向量为法向量的平面完全确定,可以表示为集合
例题讲解
练习1.
1、判断正误.(正确的画“√”,错误的画“×”)
(1)直线的方向向量是唯一的. ( )
(2)若点,是平面上的任意两点,是平面的法向量,则 .( )
(3)由空间点和直线的方向向量能表示直线上的任意一点. ( )
(4)空间中任意平面由空间一点及两个不共线向量唯一确定. ( )
2、若(2,1,1),(1,2,2)在直线上,则直线的一个方向向量为( )
(2,1,1) (-2,2,2) (-3,2,1) (2,1,-1)
答案:1、(1)× (2)√ (3)√ (4)√
答案:2、
例题讲解
例1.如图,在长方体中,是的中点.以为原点,所在直线分别为轴、轴、轴,建立如图所示的空间直角坐标系.
(1)求平面的法向量;(2)求平面的法向量.
解:(1)因为轴垂直于平面,
所以是平面的一个法向量.
例题讲解
例1.如图,在长方体中,
是的中点.以为原点,所在直线分别为轴、轴、轴,
建立如图所示的空间直角坐标系.(2)求平面的法向量.
解:(2)因为是的中点,所以,的坐标分别为,,.
因此,.
设是平面的法向量,则,
所以所以
取,则,.于是是平面的一个法向量.
利用待定系数法求法向量的步骤
设向量
设平面法向量n=(x,y,z)
列方程组
选向量
在平面内选取两个不共线向量AB,AC
取x,y,z中一个为非零值(常取±1)
赋值
结论
得到平面的一个法向量
n·AB=0
n·AC=0
列出等式
例题讲解
练习2. 已知(0,1,1),(-1,1,1),(1,0,0),则平面的一个 法向量为 ( )
.(0,1,-1) .(-1,0,1) .(1,1,1) .(-1,0,0)
解:设平面的法向量为,由,,可得
取,得, -1
选
新知探究
思考:既然点线面均可用向量表示,那是否可以利用向量进一步研究点线面间的位置关系呢?
问题4:由直线与直线的平行关系,可以得到这两条直线的方向向量有什么关系呢?
所以,
使得
新知探究
问题5:由直线与平面的平行关系,可以得到直线的方向向量与平面的法向量有什么关系呢?
新知探究
问题6:由平面与平面的平行关系,可以得到着两个平面的法向量有什么关系呢?
使得
新知探究
线面的位置关系 向量的位置关系 向量的运算 向量运算的坐标表示
∥
∥ β
使得
使得
= =
+
= =
例题讲解
例2.证明“平面与平面平行的判定定理”:若一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.
已知:如图,,,,,.
求证:
证明:如图,取平面的法向量,直线的方向向量,.
因为,,所以.
因为
所以对任意点,存在,使得.
从而.
所以,向量也是平面的法向量.故
例题讲解
例3.如图,在长方体中,.线段上是否存在点,使得平面?
解:以为原点,,,所在直线分别为轴、轴、轴,建立如图所示的空间直角坐标系.因为,,的坐标分别为,,,
所以,.
设是平面的法向量,则,,即所以
例题讲解
例3.如图,在长方体中,.线段上是否存在点,使得平面?
取,则,.
所以,是平面的一个法向量.
由,,的坐标分别为,,,得
,.
设点满足则,
所以.
令,得,解得,
此时平面,这样的点存在.
所以,当,即为的中点时,平面.
例题讲解
练习3.如图,已知正方体的棱长为2,分别是,的中点,求证:平面.
证明:建立如图所示空间直角坐标系,
则有
所以,,.
设是平面的法向量,则,,
即得令,则,
所以.因为,所以.
又因为平面,所以平面.
例题讲解
练习4.已知正方体的棱长为2,分别是,的中点,求证:平面平面.
证明:建立如图所示空间直角坐标系,则有
所以,
设是平面的法向量,则,,
即得
令,则,所以.
又平面的法向量 .
,所以平面平面.
新知探究
问题7:直线、平面间的垂直关系又如何用向量表示呢?
线线垂直
线面垂直
面面垂直
,使得
例题讲解
例4.如图,在平行六面体中,求证:直线平面.
证明:设,,,则为空间的一个基底,
且,,.
因为
所以
在平面上,取,为基向量,则对于平面上任意一点,
存在唯一的有序实数对,使得
所以,
所以是平面的法向量.所以平面.
例题讲解
例5. 证明“平面与平面垂直的判定定理”:若一个平面过另一个平面的垂线,则这两个平面垂直.
已知:如图,,求证:.
证明:取直线的方向向量,平面的法向量.
因为,所以是平面的法向量.
因为,而是平面的法向量,所以.
所以.
例题讲解
练习5.在四棱锥 中,底面 是正方形, ⊥底面 ,且 = ,
是 的中点.求证:平面 ⊥平面 .
证明:设,建立如图所示的空间直角坐标系,
设平面的法向量为
易知
∴即
令,可得平面的一个法向量为.
∵平面,∴平面的一个法向量为
∵,∴平平面.
小结
用空间向量研究直线、平面的位置关系
线面位置关系的向量表示
点线面的向量表示
点
线
面
OP=xa+yb
平面的法向量:
小结
线线平行
线面平行
面面平行
使得
使得
小结
线线垂直
线面垂直
面面垂直
,使得
