11.2.1三角形的内角同步练习 2023-2024学年人教版数学八年级上册(含答案)
文档属性
| 名称 | 11.2.1三角形的内角同步练习 2023-2024学年人教版数学八年级上册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 268.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-22 00:00:00 | ||
图片预览

文档简介
11.2.1三角形的内角 同步练习
一、单选题
1.在Rt△ABC中,BC是斜边,∠B=40°,则∠C=( )
A.90° B.60° C.50° D.40°
2.若三角形三个角的度数比为3:3:4,则这个三角形一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
3.在中,若都是锐角,则是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.以上都有可能
4.若一个三角形三个内角度数的比为2:7:1,那么这个三角形是( )
A.钝角三角形 B.直角三角形 C.锐角三角形 D.等边三角形
5.一次数学活动中,小明对纸带沿折叠,量得,则的度数是( )
A. B. C. D.
6.如图,.下列条件中能使的是 ( )
A. B.
C. D.
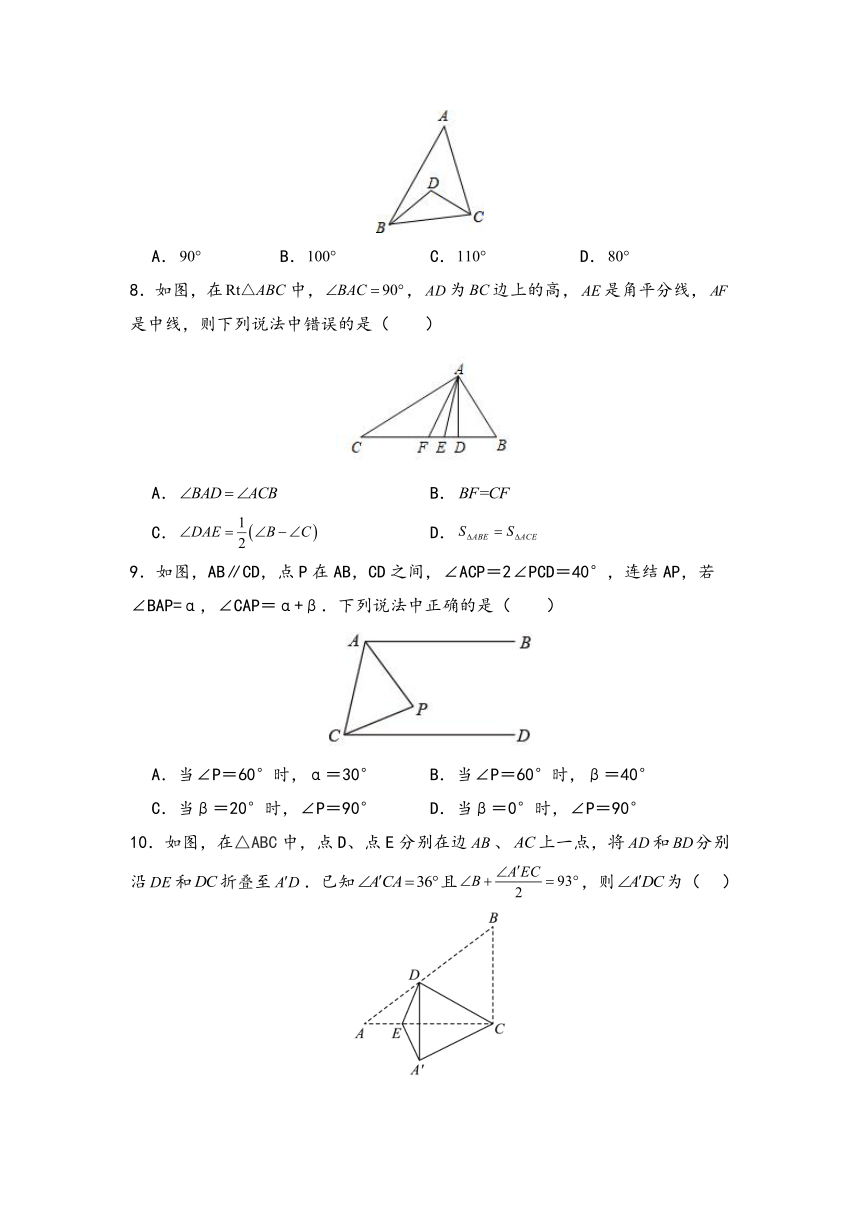
7.如图,在△ABC中,,点D是和角平分线的交点,则( )
A. B. C. D.
8.如图,在中,,为边上的高,是角平分线,是中线,则下列说法中错误的是( )
A. B.
C. D.
9.如图,AB∥CD,点P在AB,CD之间,∠ACP=2∠PCD=40°,连结AP,若∠BAP=α,∠CAP=α+β.下列说法中正确的是( )
A.当∠P=60°时,α=30° B.当∠P=60°时,β=40°
C.当β=20°时,∠P=90° D.当β=0°时,∠P=90°
10.如图,在△ABC中,点D、点E分别在边、上一点,将和分别沿和折叠至.已知且,则为( )
A. B. C. D.
二、填空题
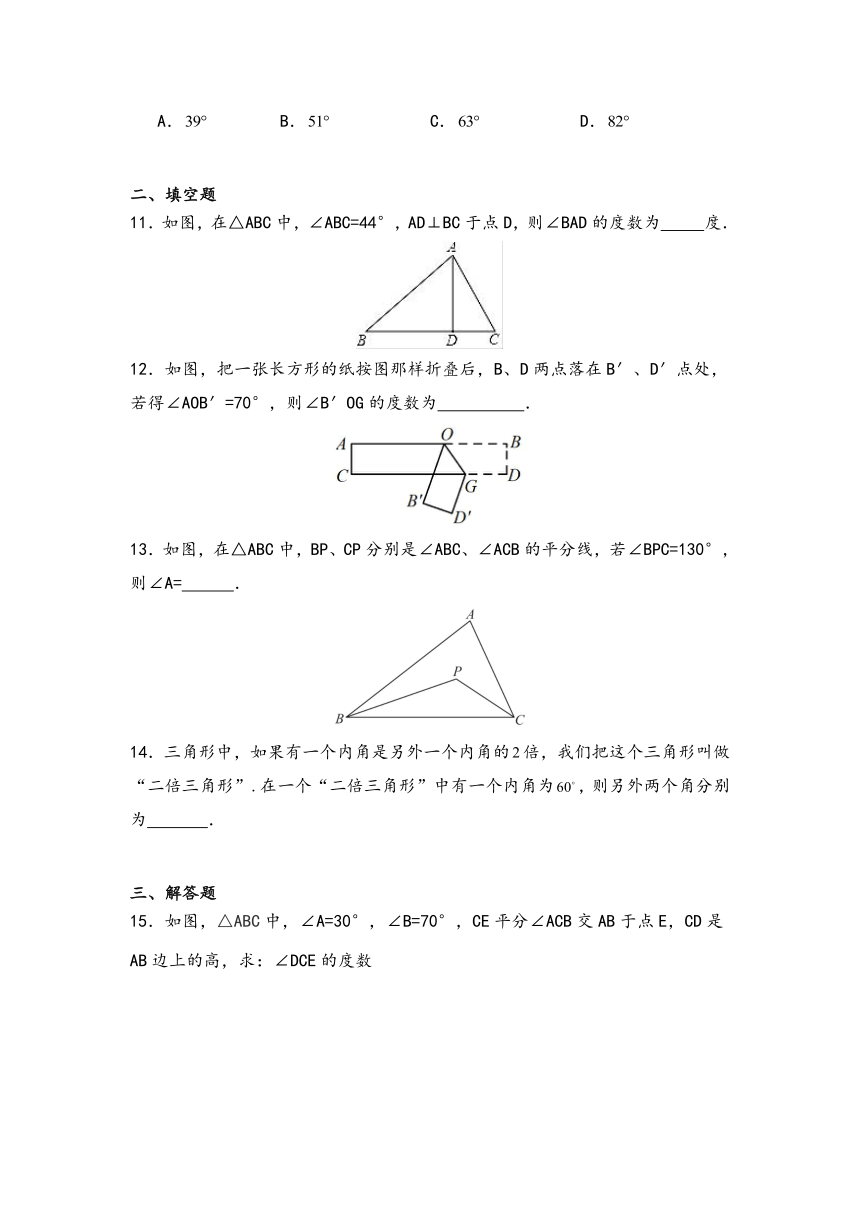
11.如图,在△ABC中,∠ABC=44°,AD⊥BC于点D,则∠BAD的度数为 度.
12.如图,把一张长方形的纸按图那样折叠后,B、D两点落在B′、D′点处,若得∠AOB′=70°,则∠B′OG的度数为 .
13.如图,在△ABC中,BP、CP分别是∠ABC、∠ACB的平分线,若∠BPC=130°,则∠A= .
14.三角形中,如果有一个内角是另外一个内角的倍,我们把这个三角形叫做“二倍三角形”.在一个“二倍三角形”中有一个内角为,则另外两个角分别为 .
三、解答题
15.如图,△ABC中,∠A=30°,∠B=70°,CE平分∠ACB交AB于点E,CD是AB边上的高,求:∠DCE的度数
16.完成下面的证明:已知:如图,,,.求证:.
证明:(已知),
∴( ),
∴在△ABC中,( ),
∵(已知),
∴,
∵,
∴ = ( ),
∴( ).
17.如图,,∠A=60°.点P是射线AM上一动点(与点A不重合),BC平分∠ABP交AM于点C,BD平分∠PBN交AM于点D.
(1)求∠ABN的度数.
(2)求∠CBD的度数.
(3)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若变化,请写出变化规律;若不变化,请写出它们之间的数量关系,并说明理由.
18.如图,平分,平分
(1)如图1,若,,求;
(2)如图2,若,,求(用,表示)
参考答案
1.C
2.A
3.D
4.A
5.C
6.B
7.C
8.D
9.B
10.B
11.46.
12.55°
13.80°/80度
14. 或
15.20°
16.垂直定义;直角三角形的两个锐角互余(或三角形的内角和为;;; 等量代换;内错角相等,两直线平行
17.(1)∵AM//BN,
∴∠A+∠ABN=180°.
∴∠ABN=180°-∠A=180°-60°=120°;
(2)∵BC平分∠ABP,BD平分∠PBN,
∴,,
∵∠CBD=∠CBP+∠PBD,
∴;
(3)不变,∠APB=2∠ADB,
∵AM//BN,
∴∠APB=∠PBN,∠ADB=∠DBN,
∵BD平分∠PBN,
∴∠PBN=2∠DBN,
∴∠APB=2∠ADB.
18.解:(1);
(2).
一、单选题
1.在Rt△ABC中,BC是斜边,∠B=40°,则∠C=( )
A.90° B.60° C.50° D.40°
2.若三角形三个角的度数比为3:3:4,则这个三角形一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
3.在中,若都是锐角,则是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.以上都有可能
4.若一个三角形三个内角度数的比为2:7:1,那么这个三角形是( )
A.钝角三角形 B.直角三角形 C.锐角三角形 D.等边三角形
5.一次数学活动中,小明对纸带沿折叠,量得,则的度数是( )
A. B. C. D.
6.如图,.下列条件中能使的是 ( )
A. B.
C. D.
7.如图,在△ABC中,,点D是和角平分线的交点,则( )
A. B. C. D.
8.如图,在中,,为边上的高,是角平分线,是中线,则下列说法中错误的是( )
A. B.
C. D.
9.如图,AB∥CD,点P在AB,CD之间,∠ACP=2∠PCD=40°,连结AP,若∠BAP=α,∠CAP=α+β.下列说法中正确的是( )
A.当∠P=60°时,α=30° B.当∠P=60°时,β=40°
C.当β=20°时,∠P=90° D.当β=0°时,∠P=90°
10.如图,在△ABC中,点D、点E分别在边、上一点,将和分别沿和折叠至.已知且,则为( )
A. B. C. D.
二、填空题
11.如图,在△ABC中,∠ABC=44°,AD⊥BC于点D,则∠BAD的度数为 度.
12.如图,把一张长方形的纸按图那样折叠后,B、D两点落在B′、D′点处,若得∠AOB′=70°,则∠B′OG的度数为 .
13.如图,在△ABC中,BP、CP分别是∠ABC、∠ACB的平分线,若∠BPC=130°,则∠A= .
14.三角形中,如果有一个内角是另外一个内角的倍,我们把这个三角形叫做“二倍三角形”.在一个“二倍三角形”中有一个内角为,则另外两个角分别为 .
三、解答题
15.如图,△ABC中,∠A=30°,∠B=70°,CE平分∠ACB交AB于点E,CD是AB边上的高,求:∠DCE的度数
16.完成下面的证明:已知:如图,,,.求证:.
证明:(已知),
∴( ),
∴在△ABC中,( ),
∵(已知),
∴,
∵,
∴ = ( ),
∴( ).
17.如图,,∠A=60°.点P是射线AM上一动点(与点A不重合),BC平分∠ABP交AM于点C,BD平分∠PBN交AM于点D.
(1)求∠ABN的度数.
(2)求∠CBD的度数.
(3)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若变化,请写出变化规律;若不变化,请写出它们之间的数量关系,并说明理由.
18.如图,平分,平分
(1)如图1,若,,求;
(2)如图2,若,,求(用,表示)
参考答案
1.C
2.A
3.D
4.A
5.C
6.B
7.C
8.D
9.B
10.B
11.46.
12.55°
13.80°/80度
14. 或
15.20°
16.垂直定义;直角三角形的两个锐角互余(或三角形的内角和为;;; 等量代换;内错角相等,两直线平行
17.(1)∵AM//BN,
∴∠A+∠ABN=180°.
∴∠ABN=180°-∠A=180°-60°=120°;
(2)∵BC平分∠ABP,BD平分∠PBN,
∴,,
∵∠CBD=∠CBP+∠PBD,
∴;
(3)不变,∠APB=2∠ADB,
∵AM//BN,
∴∠APB=∠PBN,∠ADB=∠DBN,
∵BD平分∠PBN,
∴∠PBN=2∠DBN,
∴∠APB=2∠ADB.
18.解:(1);
(2).
