7.1.2弧度制 课件(共20张PPT)
文档属性
| 名称 | 7.1.2弧度制 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-21 19:10:31 | ||
图片预览






文档简介
(共20张PPT)
弧度制
高一数学组
长度有哪些不同的度量方式
问题引入
约在公元前2000年,巴比伦人就习惯将圆周划分为360份,其中1份所对的圆心角为1度的角,记为1°. 1°=60′,1′=60″
用度做为单位来度量角的单位制叫做角度制.
1°角的大小
1°角是如何定义的?
大致可以看作以一个成年人的胳膊作半径、并以其小拇指的一个关节作弧长所对应的圆心角。
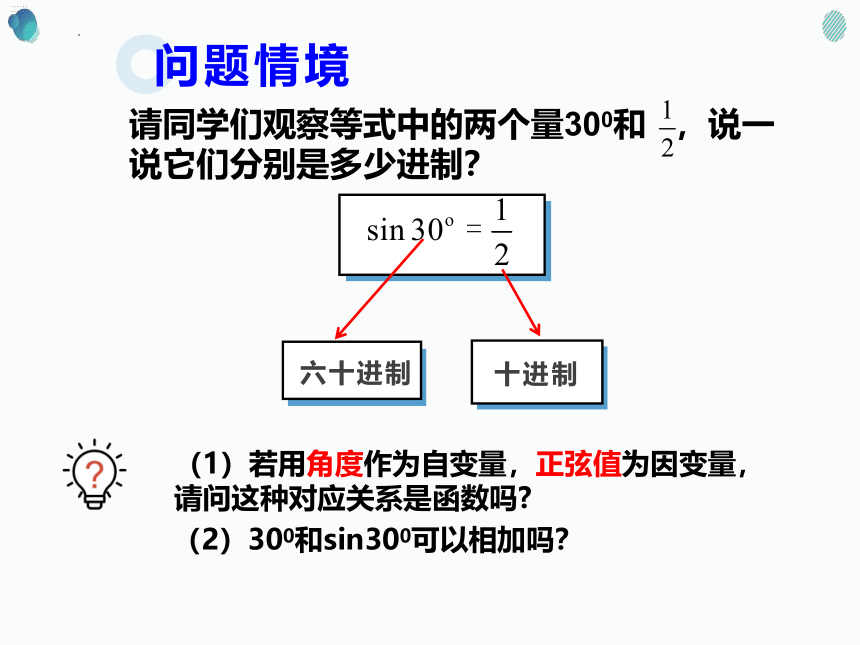
请同学们观察等式中的两个量300和 ,说一说它们分别是多少进制?
六十进制
十进制
问题情境
(1)若用角度作为自变量,正弦值为因变量,请问这种对应关系是函数吗
(2)300和sin300可以相加吗?
寻找新定义
探究1:如何把60进制的角度
转化为10进制的实数呢?
问:在图形中有哪些量与图示中的角的大小有关,
且是实数?
把长度等于半径长的弧所对的圆心角叫做
1弧度的角. 记作1rad,读作1弧度.
用弧度作为角的单位来度量角的单位制称为弧度制.
猜一猜:1弧度大约有多大?
1.定义
用弧度表示角的大小时,只要不引起误解,可以省略单位“rad”
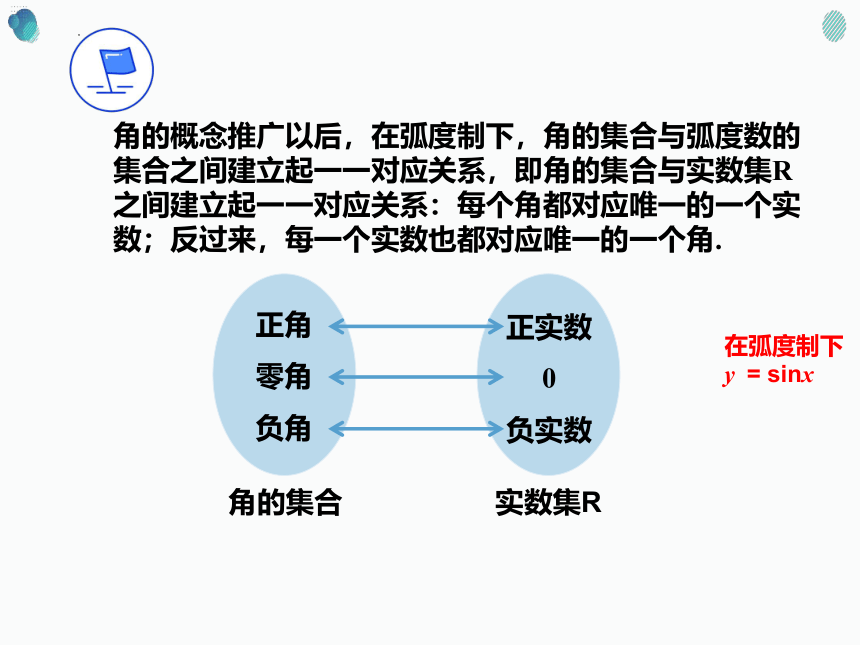
正角
零角
负角
角的集合
实数集R
正实数
0
负实数
角的概念推广以后,在弧度制下,角的集合与弧度数的集合之间建立起一一对应关系,即角的集合与实数集R之间建立起一一对应关系:每个角都对应唯一的一个实数;反过来,每一个实数也都对应唯一的一个角.
在弧度制下
y = sinx
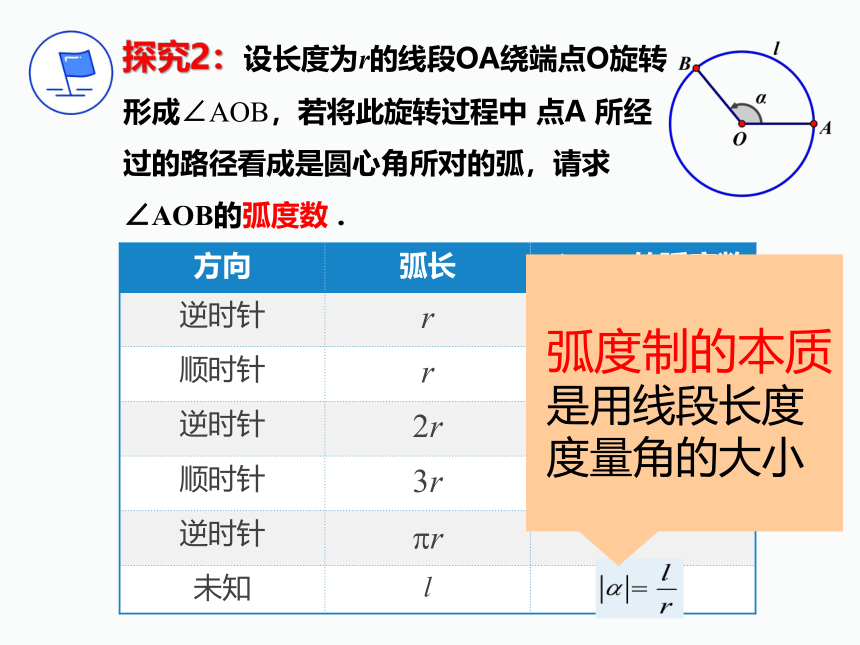
探究2:设长度为r的线段OA绕端点O旋转形成∠AOB,若将此旋转过程中 点A 所经过的路径看成是圆心角所对的弧,请求∠AOB的弧度数 .
方向 弧长 ∠AOB的弧度数
逆时针 r
顺时针 r
逆时针 2r
顺时针 3r
逆时针 pr
未知 l
1
-1
-3
p
2
弧度制的本质是用线段长度度量角的大小
弧度制和角度制都是描述角大小的方式,
请问与弧度和角度如何互化?
探究3:
360°= 2π
180°= π
1度等于多少弧度?1弧度等于多少度?
1°=
0.01745 rad
1 rad=
2. 角度与弧度的换算
360°= 2π
180°= π
练习:观察下列角与平角的关系,写出它的弧度数
360°= 2π
2. 角度与弧度的换算
度
弧度
度
弧度
请在空白处填写正确的答案
例1 把下列各角从弧度化为度:
(非特殊角)
2. 角度与弧度的换算
例2 把下列各角从度化为弧度:
2. 角度与弧度的换算
(非特殊角)
角度制 弧度制
扇形 面积
弧长
简化了有关公式及运算.
探究5:请同学们自行推导
弧度制下的弧长和扇形面积公式
r
例3 已知扇形的周长为 8 cm,圆心角为
2 rad ,求该扇形的面积.
链接
本节课你有哪些收获呢?
链接
角的单位制
百分度制:
常用于建筑或土木工程的角度测量
毫弧度:
一般用作空间分辨率的单位
密位制:
广泛用于航海和军事上
角度制
弧度制
链接
作业布置
1. 必做题:
PXX第X题
2. 选做题:
PXX第X题
3. 探究题:
请同学们到阅览室或网上查找古今中外角的弧度制的历史,整理并相互交流。
谢谢大家!
你站在操场中心,另一个人与你之间有一定的距离且绕着你沿圆周跑步,你要做的就是保持你的脸始终朝向那个人。
假设那个人跑的长度为s,根据你和那个人之间的距离 就可以计算出你的头偏转的角度。
“度数”关心的是你的头偏转的角度,
“弧度”关心的是那个人奔跑的距离。
其本质区别在于参考对象变了。
举个例子想一想
弧度制
高一数学组
长度有哪些不同的度量方式
问题引入
约在公元前2000年,巴比伦人就习惯将圆周划分为360份,其中1份所对的圆心角为1度的角,记为1°. 1°=60′,1′=60″
用度做为单位来度量角的单位制叫做角度制.
1°角的大小
1°角是如何定义的?
大致可以看作以一个成年人的胳膊作半径、并以其小拇指的一个关节作弧长所对应的圆心角。
请同学们观察等式中的两个量300和 ,说一说它们分别是多少进制?
六十进制
十进制
问题情境
(1)若用角度作为自变量,正弦值为因变量,请问这种对应关系是函数吗
(2)300和sin300可以相加吗?
寻找新定义
探究1:如何把60进制的角度
转化为10进制的实数呢?
问:在图形中有哪些量与图示中的角的大小有关,
且是实数?
把长度等于半径长的弧所对的圆心角叫做
1弧度的角. 记作1rad,读作1弧度.
用弧度作为角的单位来度量角的单位制称为弧度制.
猜一猜:1弧度大约有多大?
1.定义
用弧度表示角的大小时,只要不引起误解,可以省略单位“rad”
正角
零角
负角
角的集合
实数集R
正实数
0
负实数
角的概念推广以后,在弧度制下,角的集合与弧度数的集合之间建立起一一对应关系,即角的集合与实数集R之间建立起一一对应关系:每个角都对应唯一的一个实数;反过来,每一个实数也都对应唯一的一个角.
在弧度制下
y = sinx
探究2:设长度为r的线段OA绕端点O旋转形成∠AOB,若将此旋转过程中 点A 所经过的路径看成是圆心角所对的弧,请求∠AOB的弧度数 .
方向 弧长 ∠AOB的弧度数
逆时针 r
顺时针 r
逆时针 2r
顺时针 3r
逆时针 pr
未知 l
1
-1
-3
p
2
弧度制的本质是用线段长度度量角的大小
弧度制和角度制都是描述角大小的方式,
请问与弧度和角度如何互化?
探究3:
360°= 2π
180°= π
1度等于多少弧度?1弧度等于多少度?
1°=
0.01745 rad
1 rad=
2. 角度与弧度的换算
360°= 2π
180°= π
练习:观察下列角与平角的关系,写出它的弧度数
360°= 2π
2. 角度与弧度的换算
度
弧度
度
弧度
请在空白处填写正确的答案
例1 把下列各角从弧度化为度:
(非特殊角)
2. 角度与弧度的换算
例2 把下列各角从度化为弧度:
2. 角度与弧度的换算
(非特殊角)
角度制 弧度制
扇形 面积
弧长
简化了有关公式及运算.
探究5:请同学们自行推导
弧度制下的弧长和扇形面积公式
r
例3 已知扇形的周长为 8 cm,圆心角为
2 rad ,求该扇形的面积.
链接
本节课你有哪些收获呢?
链接
角的单位制
百分度制:
常用于建筑或土木工程的角度测量
毫弧度:
一般用作空间分辨率的单位
密位制:
广泛用于航海和军事上
角度制
弧度制
链接
作业布置
1. 必做题:
PXX第X题
2. 选做题:
PXX第X题
3. 探究题:
请同学们到阅览室或网上查找古今中外角的弧度制的历史,整理并相互交流。
谢谢大家!
你站在操场中心,另一个人与你之间有一定的距离且绕着你沿圆周跑步,你要做的就是保持你的脸始终朝向那个人。
假设那个人跑的长度为s,根据你和那个人之间的距离 就可以计算出你的头偏转的角度。
“度数”关心的是你的头偏转的角度,
“弧度”关心的是那个人奔跑的距离。
其本质区别在于参考对象变了。
举个例子想一想
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
