22.1.3 二次函数y=a(x-h)2+k的图象和性质 课件(共29张PPT)
文档属性
| 名称 | 22.1.3 二次函数y=a(x-h)2+k的图象和性质 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-21 14:46:22 | ||
图片预览



文档简介
(共29张PPT)
22.1.3二次函数y=a(x-h)2+k的图象和性质
人教版九年级上册
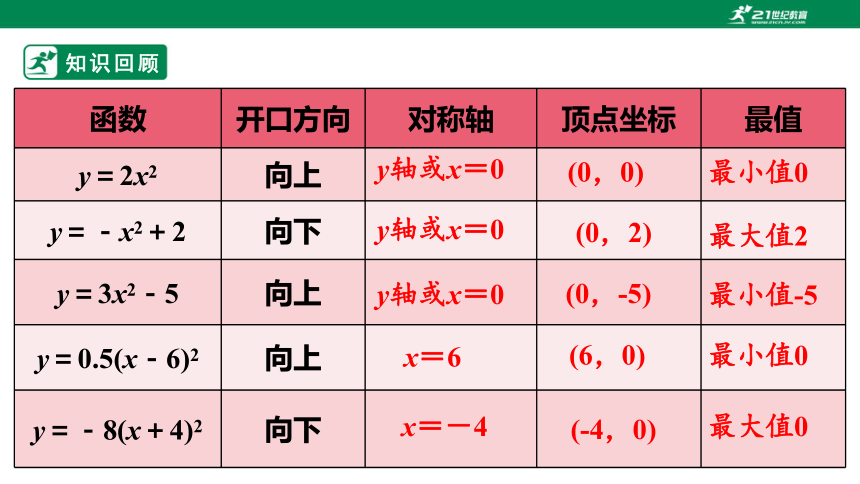
知识回顾
函数 开口方向 对称轴 顶点坐标 最值
y=2x2 向上
y=-x2+2 向下
y=3x2-5 向上
y=0.5(x-6)2 向上
y=-8(x+4)2 向下
y轴或x=0
y轴或x=0
y轴或x=0
x=6
x=-4
(0,0)
(-4,0)
(0,-5)
(6,0)
(0,2)
最大值2
最小值-5
最小值0
最小值0
最大值0
教学目标
1.会用描点法画出 y=a(x-h)2+k (a ≠0) 的图象.
2.理解二次函数y=a(x-h)2+k (a ≠0)与y=ax2 (a ≠0)图象之
间的位置关系.
3.掌握二次函数y=a(x-h)2+k (a ≠0)的图象的性质.
4.能解决与二次函数相关的实际问题
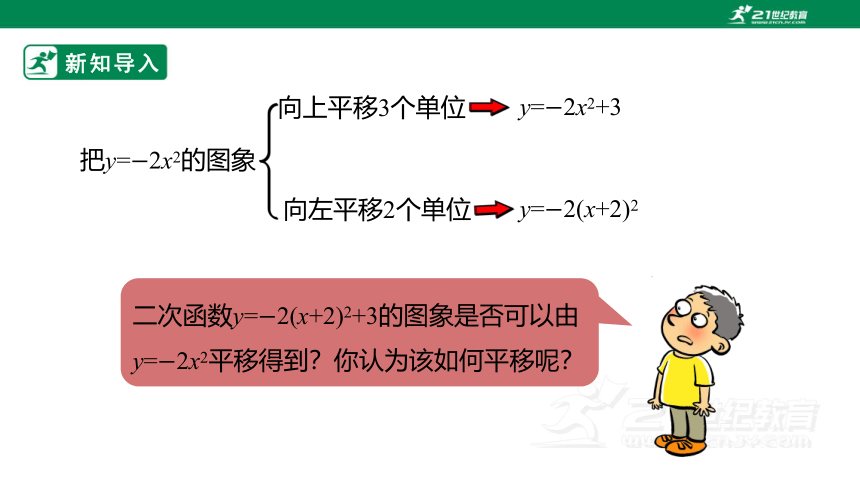
新知导入
把y= 2x2的图象
向上平移3个单位
y= 2x2+3
向左平移2个单位
y= 2(x+2)2
二次函数y= 2(x+2)2+3的图象是否可以由y= 2x2平移得到?你认为该如何平移呢?
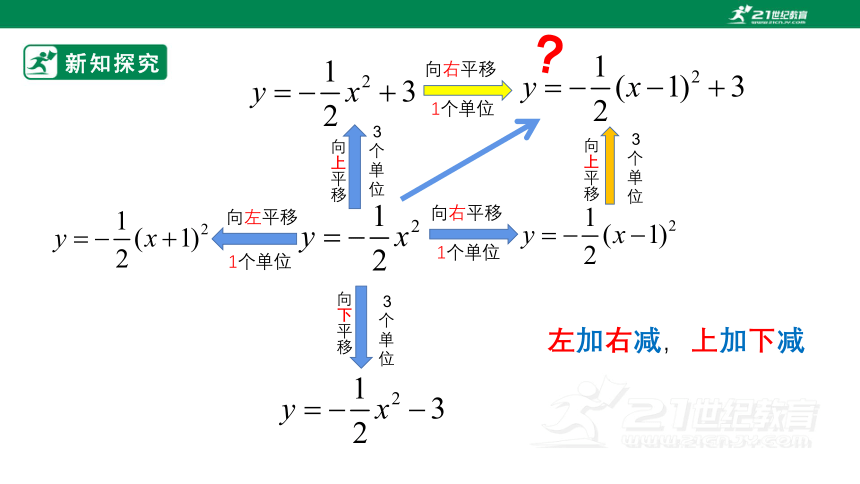
新知探究
向右平移
1个单位
向左平移
1个单位
向下平移
向上平移
向上平移
?
向右平移
1个单位
左加右减,上加下减
3
个
单
位
3
个
单
位
3
个
单
位
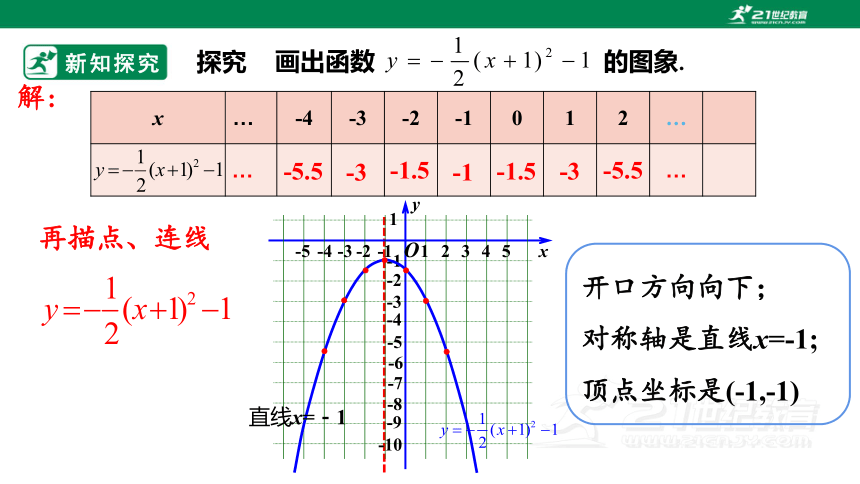
新知探究
画出函数 的图象.
…
…
…
…
2
1
0
-1
-2
-3
-4
x
解:
再描点、连线
-5.5
-3
-1.5
-1
-1.5
-3
-5.5
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
O
-1
-2
-3
-4
-5
-10
直线x=-1
开口方向向下;
对称轴是直线x=-1;
顶点坐标是(-1,-1)
探究
新知探究
函数 图象的性质.
开口方向:
顶点:
对称轴:
最值:
增减性:
向下
(1,3)
直线
(1,3)
(0,0)
新知小结
开口方向
顶点 对称轴 最值
增减性
直线
对称轴左边递减
右边递增
对称轴左边递增
右边递减
向上
向下
(顶点式)
平移
对于抛物线 y= (x+1)2+3,下列结论:
①抛物线的开口向下;②对称轴为直线x=1;
③顶点坐标为(-1,3);④当x>1时,y随x的增大而减小.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
新知典例
例1
分析:①抛物线a<0,开口向下
②抛物线h=-1,所以对称轴为直线x=-1,
③h=-1,k=3,所以顶点坐标为(-1,3)
④抛物线在对称轴右侧,y随x的增大而减小.
C
新知练习
2.二次函数 的图象开口方向是 ,
顶点坐标是 ,当 时, 随 的增大而 .
3.二次函数 的图象开口方向是 ,顶点坐
标是 ,当 时, 有最 值 ,当 时,
随 的增大而 .
向上
(3,1)
增大
向下
(-2,3)
-2
大
3
减小
新知探究
在同一坐标系中画出函数 ,
的图象.
… -2 -1 0 1 2 3 4 …
… …
… …
-2
1
0
3
-2
1
解:
新知探究
向上平移
向右平移
1个单位
3
个
单
位
当a相同时,函数解析式的变化,对应的
函数图象的变化可以通过平移来实现.
向上平移
3
个
单
位
向右平移
1个单位
新知小结
二次函数 y=ax2 与 y=a(x-h)2+k 图象间的关系
可以互相平移得到:
y = ax2
y = ax2 + k
y = a(x - h )2
y = a( x - h )2 + k
上下平移
左右平移
上下平移
左右平移
函数平移有规律,左加右减自变量,上加下减常数项.
新知典例
把二次函数y=a(x-h)2+k的图象先向左平移2个单位长度,再向上平移4个单位长度,得到二次函数y= (x+1)2-1的图象.
(1)试确定a,h,k的值;
(2)指出二次函数y=a(x-h)2+k的开口方向、对称轴和顶点坐标.
例2
解:(1)由题意,得
y=a(x-h+2)2+k+4与y= (x+1)2-1是同一函数,
所以
2-h=1,
k+4=-1,
解得 h=1,k=-5.
(2)它的开口向上,对称轴为x=1,顶点坐标为(1,-5).
新知练习
3.如图,将抛物线 先向左平移3个单位,
再向上平移2个单位,得到新的抛物线的解析
式是 .
(0,0)
(-3,2)
左移3个单位
上移2个单位
左加右减,上加下减。
方法一
方法二
由题可知y=a(x+3)2+2(a≠0)
新知探究
例3 要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为 1 m处达到最高,高度为 3 m,水柱落地处离池中心3 m,水管应多长?
A
B
C
D
E
新知探究
由题可知抛物线顶点为(1,3),所以可设抛物线解析式为
由抛物线经过点C(3,0),可得
解:如图,以水管与地面交点为原点,原点与水柱落地处所在直线
为 轴,水管所在直线为 轴,建立直角坐标系.
解得
当 时, ,也就是说,水管长2.25m.
A
B
C
D
E
新知探究
例题拓展
新知典例
例4 已知点A(1,y1),B(- ,y2),C(-2,y3)在函数y=a(x+1)2+k(a>0)的图象上,y1,y2,y3的大小关系是什么?
解:y=a(x+1)2+k(a>0)的图象是关于直线x=-1对称的抛物线,A(1,y1)关于直线x=-1的对称点是(-3,y1),
由于抛物线开口向上,在对称轴左侧y随x的增大而减小,
所以则y1>y3>y2.
新知练习
4.已知点A(4,y1),B( ,y2),C(-2,y3)都在函数y=(x-2)2-1的图象上,则y1,y2,y3的大小关系是 .
y3>y1>y2
对接中考
1.若抛物线y=(x-m)2+(m+1)的顶点在第一象限,则m的取值范围是( )
A.m>1 B.m>0 C.m>-1 D.-1<m<0
B
对接中考
-2
1
4
O
m
x
y
2.当 -2≤x≤1 时,二次函数 y=-(x-m)2+m2+1 有最大值 4,则实数 m 的值为( )
A.- B.3或- C.2或- D. 2或或-
-2
1
4
O
m
x
y
-2
1
4
O
m
x
y
对接中考
C
2.当 -2≤x≤1 时,二次函数 y=-(x-m)2+m2+1 有最大值 4,则实数 m 的值为( )
A.- B.3或- C.2或- D. 2或或-
解:二次函数的图象对称轴为直线 x=m,
①若 m<-2,则x=-2时取得最大值,-(-2-m)2+m2+1=4,
解得m=-,与m<-2矛盾,舍去;
②若 -2≤m≤1,则x=m时取得最大值,m2+1=4,
解得 m=±,因为 m=不满足-2≤m≤1的范围,所以 m=-;
③若m>1,则x=1时取得最大值,-(1-m)2+m2+1=4,解得 m=2.
综上所述,m=2或-时,二次函数有最大值4.
课堂总结
1.二次函数 与 的关系;
2.二次函数 的图象性质;
3.利用二次函数的性质解决实际问题;
位置不同,可以通过平移得到。
形状和大小相同( 相等),
主要研究:开口方向,顶点,对称轴,增减性,最值;
研究方法:关注顶点,结合函数图象来理解;
实际问题
数学问题
建立适当的坐标系
求解析式
(简洁,计算简单)
求实际问题解
(待定系数法)
课堂练习
1.对于抛物线 y=(x+2)2+3,给出下列结论:①抛物线y=(x+2)2+3 可由抛物线y=x2先向左平移 2 个单位长度,再向上平移 3 个单位长度得到;②对称轴为直线 x=2;③顶点坐标为(-2,3);④当 x>-2 时,y 随 x 的增大而增大.其中正确结论的个数为( )
C
A.1 B.2 C.3 D.4
课堂练习
2.把抛物线 y=-3x2 先向上平移 2 个单位,再向右平移 1 个单位,那么所得抛物线是___________________.
3.将抛物线 y=x2+1先向左平移 2 个单位长度,再向下平移 3 个单位长度,所得抛物线对应的函数解析式是 .
y=(x+2)2-2
课堂练习
二次函数 开口方向 对称轴 顶点坐标
y=2(x+3)2+5
向上
( 1, -2 )
向下
向下
( 3 , 7)
( 2 , -6 )
向上
直线 x=-3
直线 x=1
直线 x=3
直线 x=2
(-3, 5 )
y=-3(x-1)2-2
y = 4(x-3)2+7
y=-5(2-x)2-6
4.完成下列表格:
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
22.1.3二次函数y=a(x-h)2+k的图象和性质
人教版九年级上册
知识回顾
函数 开口方向 对称轴 顶点坐标 最值
y=2x2 向上
y=-x2+2 向下
y=3x2-5 向上
y=0.5(x-6)2 向上
y=-8(x+4)2 向下
y轴或x=0
y轴或x=0
y轴或x=0
x=6
x=-4
(0,0)
(-4,0)
(0,-5)
(6,0)
(0,2)
最大值2
最小值-5
最小值0
最小值0
最大值0
教学目标
1.会用描点法画出 y=a(x-h)2+k (a ≠0) 的图象.
2.理解二次函数y=a(x-h)2+k (a ≠0)与y=ax2 (a ≠0)图象之
间的位置关系.
3.掌握二次函数y=a(x-h)2+k (a ≠0)的图象的性质.
4.能解决与二次函数相关的实际问题
新知导入
把y= 2x2的图象
向上平移3个单位
y= 2x2+3
向左平移2个单位
y= 2(x+2)2
二次函数y= 2(x+2)2+3的图象是否可以由y= 2x2平移得到?你认为该如何平移呢?
新知探究
向右平移
1个单位
向左平移
1个单位
向下平移
向上平移
向上平移
?
向右平移
1个单位
左加右减,上加下减
3
个
单
位
3
个
单
位
3
个
单
位
新知探究
画出函数 的图象.
…
…
…
…
2
1
0
-1
-2
-3
-4
x
解:
再描点、连线
-5.5
-3
-1.5
-1
-1.5
-3
-5.5
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
O
-1
-2
-3
-4
-5
-10
直线x=-1
开口方向向下;
对称轴是直线x=-1;
顶点坐标是(-1,-1)
探究
新知探究
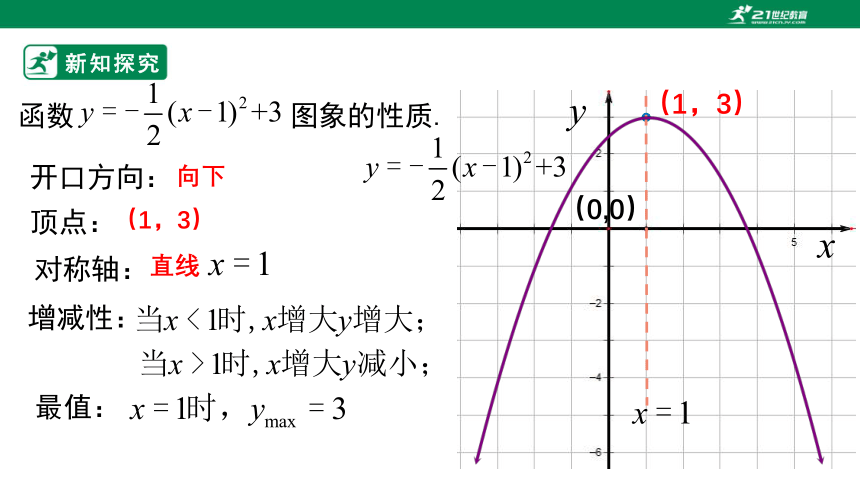
函数 图象的性质.
开口方向:
顶点:
对称轴:
最值:
增减性:
向下
(1,3)
直线
(1,3)
(0,0)
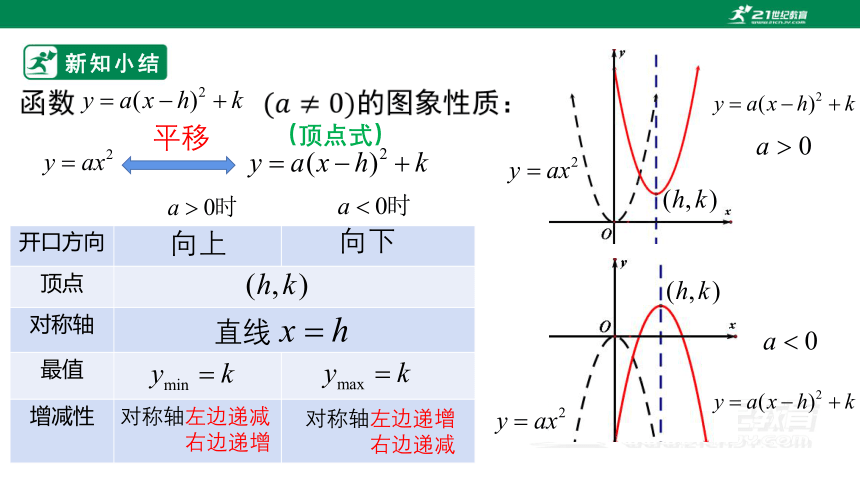
新知小结
开口方向
顶点 对称轴 最值
增减性
直线
对称轴左边递减
右边递增
对称轴左边递增
右边递减
向上
向下
(顶点式)
平移
对于抛物线 y= (x+1)2+3,下列结论:
①抛物线的开口向下;②对称轴为直线x=1;
③顶点坐标为(-1,3);④当x>1时,y随x的增大而减小.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
新知典例
例1
分析:①抛物线a<0,开口向下
②抛物线h=-1,所以对称轴为直线x=-1,
③h=-1,k=3,所以顶点坐标为(-1,3)
④抛物线在对称轴右侧,y随x的增大而减小.
C
新知练习
2.二次函数 的图象开口方向是 ,
顶点坐标是 ,当 时, 随 的增大而 .
3.二次函数 的图象开口方向是 ,顶点坐
标是 ,当 时, 有最 值 ,当 时,
随 的增大而 .
向上
(3,1)
增大
向下
(-2,3)
-2
大
3
减小
新知探究
在同一坐标系中画出函数 ,
的图象.
… -2 -1 0 1 2 3 4 …
… …
… …
-2
1
0
3
-2
1
解:
新知探究
向上平移
向右平移
1个单位
3
个
单
位
当a相同时,函数解析式的变化,对应的
函数图象的变化可以通过平移来实现.
向上平移
3
个
单
位
向右平移
1个单位
新知小结
二次函数 y=ax2 与 y=a(x-h)2+k 图象间的关系
可以互相平移得到:
y = ax2
y = ax2 + k
y = a(x - h )2
y = a( x - h )2 + k
上下平移
左右平移
上下平移
左右平移
函数平移有规律,左加右减自变量,上加下减常数项.
新知典例
把二次函数y=a(x-h)2+k的图象先向左平移2个单位长度,再向上平移4个单位长度,得到二次函数y= (x+1)2-1的图象.
(1)试确定a,h,k的值;
(2)指出二次函数y=a(x-h)2+k的开口方向、对称轴和顶点坐标.
例2
解:(1)由题意,得
y=a(x-h+2)2+k+4与y= (x+1)2-1是同一函数,
所以
2-h=1,
k+4=-1,
解得 h=1,k=-5.
(2)它的开口向上,对称轴为x=1,顶点坐标为(1,-5).
新知练习
3.如图,将抛物线 先向左平移3个单位,
再向上平移2个单位,得到新的抛物线的解析
式是 .
(0,0)
(-3,2)
左移3个单位
上移2个单位
左加右减,上加下减。
方法一
方法二
由题可知y=a(x+3)2+2(a≠0)
新知探究
例3 要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为 1 m处达到最高,高度为 3 m,水柱落地处离池中心3 m,水管应多长?
A
B
C
D
E
新知探究
由题可知抛物线顶点为(1,3),所以可设抛物线解析式为
由抛物线经过点C(3,0),可得
解:如图,以水管与地面交点为原点,原点与水柱落地处所在直线
为 轴,水管所在直线为 轴,建立直角坐标系.
解得
当 时, ,也就是说,水管长2.25m.
A
B
C
D
E
新知探究
例题拓展
新知典例
例4 已知点A(1,y1),B(- ,y2),C(-2,y3)在函数y=a(x+1)2+k(a>0)的图象上,y1,y2,y3的大小关系是什么?
解:y=a(x+1)2+k(a>0)的图象是关于直线x=-1对称的抛物线,A(1,y1)关于直线x=-1的对称点是(-3,y1),
由于抛物线开口向上,在对称轴左侧y随x的增大而减小,
所以则y1>y3>y2.
新知练习
4.已知点A(4,y1),B( ,y2),C(-2,y3)都在函数y=(x-2)2-1的图象上,则y1,y2,y3的大小关系是 .
y3>y1>y2
对接中考
1.若抛物线y=(x-m)2+(m+1)的顶点在第一象限,则m的取值范围是( )
A.m>1 B.m>0 C.m>-1 D.-1<m<0
B
对接中考
-2
1
4
O
m
x
y
2.当 -2≤x≤1 时,二次函数 y=-(x-m)2+m2+1 有最大值 4,则实数 m 的值为( )
A.- B.3或- C.2或- D. 2或或-
-2
1
4
O
m
x
y
-2
1
4
O
m
x
y
对接中考
C
2.当 -2≤x≤1 时,二次函数 y=-(x-m)2+m2+1 有最大值 4,则实数 m 的值为( )
A.- B.3或- C.2或- D. 2或或-
解:二次函数的图象对称轴为直线 x=m,
①若 m<-2,则x=-2时取得最大值,-(-2-m)2+m2+1=4,
解得m=-,与m<-2矛盾,舍去;
②若 -2≤m≤1,则x=m时取得最大值,m2+1=4,
解得 m=±,因为 m=不满足-2≤m≤1的范围,所以 m=-;
③若m>1,则x=1时取得最大值,-(1-m)2+m2+1=4,解得 m=2.
综上所述,m=2或-时,二次函数有最大值4.
课堂总结
1.二次函数 与 的关系;
2.二次函数 的图象性质;
3.利用二次函数的性质解决实际问题;
位置不同,可以通过平移得到。
形状和大小相同( 相等),
主要研究:开口方向,顶点,对称轴,增减性,最值;
研究方法:关注顶点,结合函数图象来理解;
实际问题
数学问题
建立适当的坐标系
求解析式
(简洁,计算简单)
求实际问题解
(待定系数法)
课堂练习
1.对于抛物线 y=(x+2)2+3,给出下列结论:①抛物线y=(x+2)2+3 可由抛物线y=x2先向左平移 2 个单位长度,再向上平移 3 个单位长度得到;②对称轴为直线 x=2;③顶点坐标为(-2,3);④当 x>-2 时,y 随 x 的增大而增大.其中正确结论的个数为( )
C
A.1 B.2 C.3 D.4
课堂练习
2.把抛物线 y=-3x2 先向上平移 2 个单位,再向右平移 1 个单位,那么所得抛物线是___________________.
3.将抛物线 y=x2+1先向左平移 2 个单位长度,再向下平移 3 个单位长度,所得抛物线对应的函数解析式是 .
y=(x+2)2-2
课堂练习
二次函数 开口方向 对称轴 顶点坐标
y=2(x+3)2+5
向上
( 1, -2 )
向下
向下
( 3 , 7)
( 2 , -6 )
向上
直线 x=-3
直线 x=1
直线 x=3
直线 x=2
(-3, 5 )
y=-3(x-1)2-2
y = 4(x-3)2+7
y=-5(2-x)2-6
4.完成下列表格:
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
